A Rock Dropped Downward

Example 2-11 A Rock Dropped Downward

For a guided interactive solution, go to Web Example 2-11 at www.wiley.com/college/touger

A rock is dropped into a 200-m-deep mine shaft. How long does it take

a.
to fall halfway to the bottom?

b.
to hit bottom?

Brief Solution

Assumptions. The rock is dropped, not thrown, so it starts from rest (v_o = 0). We choose the rock's starting position to be the origin (y = y_o = 0), the starting instant to be t = 0, and the downward direction to be negative. Then the bottom of the shaft is at y = −200 m, and halfway down is y = −100 m.

Restating the question. In Form 2-1, the questions become

a.
t = ? when y = −100 m

b.
t = ? when y = −200 m.

What we know/what we don't.

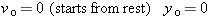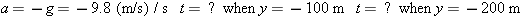Choice of approach. The constant acceleration equations of motion are convenient to use here.

The mathematical solution. With v_o = 0, y_o = 0, and a = −g, Equation 2-11 becomes 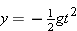. Solving for t and substituting the values for part a gives

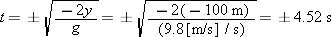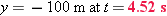We choose the positive root because the rock is falling only when t ≥ 0. Thus,

Will it take twice as long to fall twice as far?
Doing the calculation for b in the same way, we get

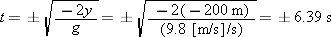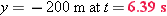so

The position y is proportional to t², not t, so it takes less than twice the time to fall twice the distance.

Related homework: Problems 2-44, 2-47, and 2-48.