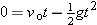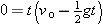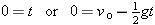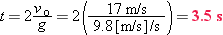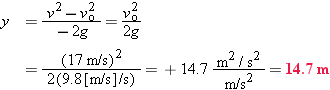A softball player throws a ball straight upward with a velocity of 17 m/s, and catches it exactly where it left her hand.
|
a. |
How long does the ball remain in the air? |
|
b. |
How high does it go? |
Solution
Assumptions. We take the origin to be the point where the ball leaves her hand. We assume that effects like air resistance are negligible, so that the ball is in free fall.
Restating the problem. The ball remains in the air until it is back where it started—at y = 0. Part a therefore asks
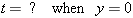 |
Part b, similarly to Example 2-9, asks
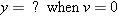 |
What we know/what we don't. In addition to this restatement of the question of the question, we know that
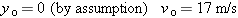 |
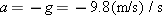 |
Choice of approach.
Again, we may apply the constant acceleration equations of motion. For part a, the equation relating y and t is Equation 2-11, written as 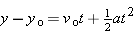 . If y is known, t will be the only unknown.
. If y is known, t will be the only unknown.
For part b, we apply Equation 2-12, written as 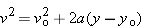 for vertical motion, to obtain a one-step solution.
for vertical motion, to obtain a one-step solution.
The mathematical solution.
|
a. |
When y = yo = 0 and a = −g, Equation 2-11 becomes
|
||||
|
b. |
With yo = 0 and a = −g, 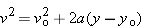 becomes becomes 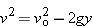 . Proceeding much as in Example 2-9, when v = 0 we get . Proceeding much as in Example 2-9, when v = 0 we get
|
||||