2-7
Gravitational Acceleration and Free Fall

When an object's fall to Earth is not helped or opposed by anything else, not even air resistance, we say the object is freely falling or in free fall. If you drop a dense, heavy object from rest and monitor its fall with a sonic range finder, you will find that the object has uniform acceleration. Moreover, you will find the value of the acceleration to be very nearly 9.8 (m/s)/s or 9.8 m/s2. This value is called its gravitational acceleration.

If you drop this textbook, the acceleration will have approximately that value. If you drop a single sheet of paper, in contrast, you will find that the acceleration is not uniform and is on average much less than 9.8 m/s2, so that the sheet of paper takes much longer to reach the ground. If you crumple the sheet of paper into a ball before dropping it, you reduce the effect of air resistance, and the paper falls more nearly like the textbook.

On-The-Spot  Activity 2-1

Take a smooth sheet of paper, small enough so that it doesn't extend beyond the edges of the cover of this book, and hold it to the underside of the book, as in Figure 2-20a. Hold the book and paper horizontally and release them together. The book and the sheet of the paper should hit the ground together. Under these circumstances, their accelerations are the same.

Figure 2-20  Comparing the accelerations of falling objects when air resistance is negligible.

“Big deal!” you say. The book is making the paper move with it. But what if you hold the sheet of paper flat on top of the book, as in Figure 2-20b, and drop it again? First decide what you think will happen to the paper, then try it. Does the paper do what you expected? If not, why not?

When air resistance is prevented from affecting the sheet of paper, the paper falls with the same acceleration as the book, roughly 9.8 m/s2.

Dropped simultaneously from the same height, bodies in free fall will hit level ground at the same time. A hammer and a feather did exactly that when they were dropped in the airless conditions on the moon by a member of the 1971 Apollo 15 mission. In another dramatic demonstration in place for many years at the Boston Museum of Science, feathers released inside a two-story glass column would drop to the bottom like the proverbial ton of bricks when the air was pumped out. Over short distances above or below Earth's surface (a few hundred meters or less), the acceleration of a freely falling body will vary with height by less than one part in a thousand. To two-place accuracy, it remains 9.8 m/s2. We use g as a symbol for this special value.

Important: The symbol g stands for this positive number, no matter which direction we call positive. When we take the positive direction to be upward, the acceleration a = −g; that is, a = −9.8 m/s2.

Applying the Constant Acceleration Equations of Motion to Free Fall

1.  

 If you choose the positive direction to be upward, let a = −g in all the equations (let a = +g if you let downward be positive).

2.  

 Because we tend to label the vertical axis y, it is common—though not necessary—to replace x with y in all the equations to indicate vertical position.

By these two steps, you should be able to show whenever needed (rather than memorize more equations) that Equations 2-9, 2-11, and 2-12 become

Try working with these ideas now in the following example.

Example 2-11 A Rock Dropped Downward
For a guided interactive solution, go to Web Example 2-11 at www.wiley.com/college/touger

A rock is dropped into a 200-m-deep mine shaft. How long does it take

a.  

 to fall halfway to the bottom?

b.  

 to hit bottom?

Brief Solution

Assumptions. The rock is dropped, not thrown, so it starts from rest (vo = 0). We choose the rock's starting position to be the origin (y = yo = 0), the starting instant to be t = 0, and the downward direction to be negative. Then the bottom of the shaft is at y = −200 m, and halfway down is y = −100 m.

Restating the question. In Form 2-1, the questions become

a.  

 t = ? when y = −100 m

b.  

 t = ? when y = −200 m.

What we know/what we don't.

Choice of approach. The constant acceleration equations of motion are convenient to use here.

The mathematical solution. With vo = 0, yo = 0, and a = −g, Equation 2-11 becomes . Solving for t and substituting the values for part a gives

We choose the positive root because the rock is falling only when t ≥ 0. Thus,

  Will it take twice as long to fall twice as far?   

Doing the calculation for b in the same way, we get

so

The position y is proportional to t2, not t, so it takes less than twice the time to fall twice the distance.

 Related homework: Problems 2-44, 2-47, and 2-48.

A note on language: Downward is not the same direction for someone in New York as for someone in Hong Kong. Wherever you are, downward means toward the center of the Earth.

Example 2-11 can also be done starting with basic definitions (see Problem 2-96).

 Other Values of g  Objects near the surface of the moon or another heavenly body (e.g., a planet or one of its moons) may also be freely falling, but not with the same acceleration. The value of g is different at each body's surface. For example, 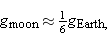and . The value of g will also vary from location to location on Earth's surface. For example, for cities at different elevations, gDenver = 9.796 m/s2, but gNew York = 9.803 m/s2. For sites at different latitudes, gEquator = 9.78 m/s2, but gNorth Pole = 9.83 m/s2. These are observed values—they come from measurements. We will not be able to address reasons for these values until we treat gravitational forces. At this point, we are only describing how objects move, not asking why they move that way.

We have said that an object is in free fall when only the gravitational pull of Earth is affecting its motion. By this definition, a ball thrown straight up is in free fall from the instant it leaves the thrower's hand, even while it is on its way up (carefully examine Figure 2-21). A sonic range finder would show that its acceleration remains constant at −9.8 m/s2 from that instant until it lands. Because the acceleration is negative, the velocity first becomes less and less positive, then more and more negative, just as was true for the ball in Example 2-8.

Figure 2-21  Motion graphs for the ball thrown upward in Example 2-12. The ball is in free fall, so that the constant acceleration equations are applicable, only between the instant it leaves the hand and the instant when it is again makes contact with the hand.

Example 2-12 A Ball Thrown Upward

A softball player throws a ball straight upward with a velocity of 17 m/s, and catches it exactly where it left her hand.

a.  

 How long does the ball remain in the air?

b.  

 How high does it go?

Solution

Assumptions. We take the origin to be the point where the ball leaves her hand. We assume that effects like air resistance are negligible, so that the ball is in free fall.

Restating the problem. The ball remains in the air until it is back where it started—at y = 0. Part a therefore asks

Part b, similarly to Example 2-9, asks

What we know/what we don't. In addition to this restatement of the question of the question, we know that

and because the ball is falling freely,

Choice of approach. Again, we may apply the constant acceleration equations of motion. For part a, the equation relating y and t is Equation 2-11, written as . If y is known, t will be the only unknown.

For part b, we apply Equation 2-12, written as for vertical motion, to obtain a one-step solution.

The mathematical solution.

a.  

 When y = yo = 0 and a = −g, Equation 2-11 becomes

This is a quadratic equation that can be solved for t by factoring:

so that either one or the other factor must be 0:

in which case, solving for t gives

There are two solutions for t, and both have meaning in the actual situation. The ball is at y = 0 first at t = 0 when it leaves the player's hand, then again at t = 3.5 s when it returns to her glove. The second solution answers the question of how long the ball remains in the air. (In fact, for any value of y, Equation 2-11 yields two solutions for t because as Figure 2-21a shows, the ball passes each value of y, other than the maximum value, both on the way up and on the way down.)

b.  

 With yo = 0 and a = −g, becomes . Proceeding much as in Example 2-9, when v = 0 we get


 Related homework: Problems 2-49 and 2-102.



Copyright © 2004 by John Wiley & Sons, Inc. or related companies. All rights reserved.