The velocity of a moving object may change in a number of ways. For example, it may increase, as it does when the driver of a car steps on the gas pedal to pass the car ahead. Or it may decrease, as it does when the driver applies the brakes to stop at a red light. In either case, the change in velocity may occur over a short or a long time interval.
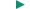 CONCEPTS AT A GLANCE To describe how the velocity of an object changes during a given time interval, we now introduce the new idea of acceleration. As the Concepts-at-a-Glance chart in Figure 2.5 illustrates, this idea depends on two concepts that we have previously encountered, velocity and time. Specifically, the notion of acceleration emerges when the change in the velocity is combined with the time during which the change occurs.
CONCEPTS AT A GLANCE To describe how the velocity of an object changes during a given time interval, we now introduce the new idea of acceleration. As the Concepts-at-a-Glance chart in Figure 2.5 illustrates, this idea depends on two concepts that we have previously encountered, velocity and time. Specifically, the notion of acceleration emerges when the change in the velocity is combined with the time during which the change occurs.
|
| Figure 2.5
CONCEPTS AT A GLANCE To formulate the concept of acceleration, the change in velocity is combined with the time required for the change to occur. As speed skater Jennifer Rodriguez competes in this race, she is accelerating when her velocity is changing. (© Ed Purcell/Aurora & Quanta Productions) |
|
The meaning of average acceleration can be illustrated by considering a plane during takeoff. Figure 2.6 focuses attention on how the plane’s velocity changes along the runway. During an elapsed time interval Dt =
= t
t –
– t0, the velocity changes from an initial value of v0 to a final value of v. The change Dv in the plane’s velocity is its final velocity minus its initial velocity, so that Dv
t0, the velocity changes from an initial value of v0 to a final value of v. The change Dv in the plane’s velocity is its final velocity minus its initial velocity, so that Dv =
= v
v –
– v0. The average acceleration
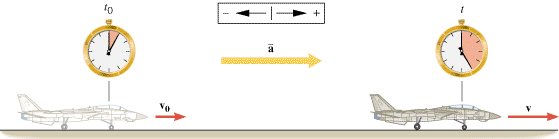
v0. The average acceleration  is defined in the following manner, to provide a measure of how much the velocity changes per unit of elapsed time.
is defined in the following manner, to provide a measure of how much the velocity changes per unit of elapsed time.
 | Figure 2.6
During takeoff, the plane accelerates from an initial velocity v0 to a final velocity v during the time interval Dt = = t t – – t0. t0.
|
|
| Definition |
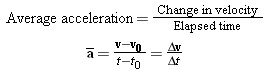 | (2.4) |  |
SI Unit of Average Acceleration: meter per second squared (m/s2)
|
The average acceleration  is a vector that points in the same direction as Dv, the change in the velocity. Following the usual custom, plus and minus signs indicate the two possible directions for the acceleration vector when the motion is along a straight line.
is a vector that points in the same direction as Dv, the change in the velocity. Following the usual custom, plus and minus signs indicate the two possible directions for the acceleration vector when the motion is along a straight line.
We are often interested in an object’s acceleration at a particular instant of time. The instantaneous acceleration a can be defined by analogy with the procedure used in Section 2.2 for instantaneous velocity:
 | (2.5) |  |
Equation 2.5 indicates that the instantaneous acceleration is a limiting case of the average acceleration. When the time interval Dt for measuring the acceleration becomes extremely small (approaching zero in the limit), the average acceleration and the instantaneous acceleration become equal. Moreover, in many situations the acceleration is constant, so the acceleration has the same value at any instant of time. In the future, we will use the word acceleration to mean “instantaneous acceleration.” Example 3 deals with the acceleration of a plane during takeoff.
 | | These thoroughbreds accelerate out of the starting gate. (© Robert Maass/Corbis Images) |
|
Problem solving insight
The change in any variable is the final value minus the initial value: for example, the change in velocity is Dv = = v v – – v0, and the change in time is Dt v0, and the change in time is Dt = = t t – – t0. t0. |
|
| Example 3 Acceleration and Increasing Velocity |
The average acceleration calculated in Example 3 is read as “nine kilometers per hour per second.” Assuming the acceleration of the plane is constant, a value of  means the velocity changes by +9.0 km/h during each second of the motion. During the first second, the velocity increases from 0 to 9.0 km/h; during the next second, the velocity increases by another 9.0 km/h to 18 km/h, and so on. Figure 2.7 illustrates how the velocity changes during the first two seconds. By the end of the 29th second, the velocity is 260 km/h.
means the velocity changes by +9.0 km/h during each second of the motion. During the first second, the velocity increases from 0 to 9.0 km/h; during the next second, the velocity increases by another 9.0 km/h to 18 km/h, and so on. Figure 2.7 illustrates how the velocity changes during the first two seconds. By the end of the 29th second, the velocity is 260 km/h.
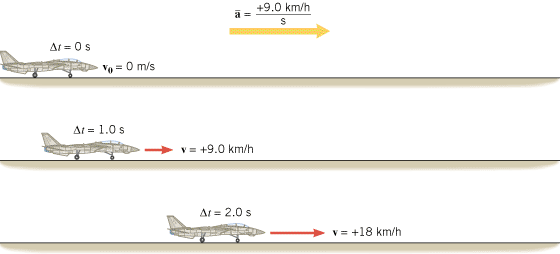 | Figure 2.7
An acceleration of  means that the velocity of the plane changes by 19.0 km/h during each second of the motion. The “+” direction for a and v is to the right. means that the velocity of the plane changes by 19.0 km/h during each second of the motion. The “+” direction for a and v is to the right. |
|
It is customary to express the units for acceleration solely in terms of SI units. One way to obtain SI units for the acceleration in Example 3 is to convert the velocity units from km/h to m/s:
The average acceleration then becomes
where we have used  . An acceleration of
. An acceleration of  is read as “2.5 meters per second per second” (or “2.5 meters per second squared”) and means that the velocity changes by 2.5 m/s during each second of the motion.
is read as “2.5 meters per second per second” (or “2.5 meters per second squared”) and means that the velocity changes by 2.5 m/s during each second of the motion.
Example 4 deals with a case where the motion becomes slower as time passes.
| Example 4 Acceleration and Decreasing Velocity |
 |
|
A drag racer crosses the finish line, and the driver deploys a parachute and applies the brakes to slow down, as Figure 2.8 illustrates. The driver begins slowing down when t0 = = 9.0 s and the car’s velocity is v0 9.0 s and the car’s velocity is v0 = = +28 m/s. When t +28 m/s. When t = = 12.0 s, the velocity has been reduced to v 12.0 s, the velocity has been reduced to v = = +13 m/s. What is the average acceleration of the dragster? +13 m/s. What is the average acceleration of the dragster?
| Figure 2.8
(a) To slow down, a drag racer deploys a parachute and applies the brakes. (b) The velocity of the car is decreasing, giving rise to an average acceleration  that points opposite to the velocity. (© Geoff Stunkard) that points opposite to the velocity. (© Geoff Stunkard) |
|
Reasoning
The average acceleration of an object is always specified as its change in velocity, v – – v0, divided by the elapsed time, t v0, divided by the elapsed time, t – – t0. This is true whether the final velocity is less than the initial velocity or greater than the initial velocity. t0. This is true whether the final velocity is less than the initial velocity or greater than the initial velocity.
Solution
The average acceleration is, according to Equation 2.4,
|
 |
Figure 2.9 shows how the velocity of the dragster changes during the braking, assuming that the acceleration is constant throughout the motion. The acceleration calculated in Example 4 is negative, indicating that the acceleration points to the left in the drawing. As a result, the acceleration and the velocity point in opposite directions. Whenever the acceleration and velocity vectors have opposite directions, the object slows down and is said to be “decelerating.” In contrast, the acceleration and velocity vectors in Figure 2.7 point in the same direction, and the object speeds up.
 | | Figure 2.9
Here, an acceleration of –5.0 m/s2 means the velocity decreases by 5.0 m/s during each second of elapsed time. |
|
| Check Your Understanding 2 |
 |
|
Two cars are moving on straight sections of a highway. The acceleration of the first car is greater than the acceleration of the second car, and both accelerations have the same direction. Which one of the following is true? (a) The velocity of the first car is always greater than the velocity of the second car. (b) The velocity of the second car is always greater than the velocity of the first car. (c) In the same time interval, the velocity of the first car changes by a greater amount than the velocity of the second car does. (d) In the same time interval, the velocity of the second car changes by a greater amount than the velocity of the first car does.
Background:
Velocity and acceleration are the focus of this question. They are not the same concept.
For similar questions (including calculational counterparts), consult Self-Assessment Test 2.1. The test is described at the end of this section.
|
|
 |
 |
|
Test your understanding of the key concepts in Sections 2.1, 2.2 and 2.3:
· Displacement · Velocity · Acceleration
|
|
 |
 |
| Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved. |
![]() CONCEPTS AT A GLANCE To describe how the velocity of an object changes during a given time interval, we now introduce the new idea of acceleration. As the Concepts-at-a-Glance chart in Figure 2.5 illustrates, this idea depends on two concepts that we have previously encountered, velocity and time. Specifically, the notion of acceleration emerges when the change in the velocity is combined with the time during which the change occurs.
CONCEPTS AT A GLANCE To describe how the velocity of an object changes during a given time interval, we now introduce the new idea of acceleration. As the Concepts-at-a-Glance chart in Figure 2.5 illustrates, this idea depends on two concepts that we have previously encountered, velocity and time. Specifically, the notion of acceleration emerges when the change in the velocity is combined with the time during which the change occurs.![]() =
=![]() t
t![]() –
–![]() t0, the velocity changes from an initial value of v0 to a final value of v. The change Dv in the plane’s velocity is its final velocity minus its initial velocity, so that Dv
t0, the velocity changes from an initial value of v0 to a final value of v. The change Dv in the plane’s velocity is its final velocity minus its initial velocity, so that Dv![]() =
=![]() v
v![]() –
–![]() v0. The average acceleration
v0. The average acceleration  is defined in the following manner, to provide a measure of how much the velocity changes per unit of elapsed time.
is defined in the following manner, to provide a measure of how much the velocity changes per unit of elapsed time.
 is a vector that points in the same direction as Dv, the change in the velocity. Following the usual custom, plus and minus signs indicate the two possible directions for the acceleration vector when the motion is along a straight line.
is a vector that points in the same direction as Dv, the change in the velocity. Following the usual custom, plus and minus signs indicate the two possible directions for the acceleration vector when the motion is along a straight line.

 means the velocity changes by +9.0 km/h during each second of the motion. During the first second, the velocity increases from 0 to 9.0 km/h; during the next second, the velocity increases by another 9.0 km/h to 18 km/h, and so on. Figure 2.7 illustrates how the velocity changes during the first two seconds. By the end of the 29th second, the velocity is 260 km/h.
means the velocity changes by +9.0 km/h during each second of the motion. During the first second, the velocity increases from 0 to 9.0 km/h; during the next second, the velocity increases by another 9.0 km/h to 18 km/h, and so on. Figure 2.7 illustrates how the velocity changes during the first two seconds. By the end of the 29th second, the velocity is 260 km/h.


 . An acceleration of
. An acceleration of  is read as “2.5 meters per second per second” (or “2.5 meters per second squared”) and means that the velocity changes by 2.5 m/s during each second of the motion.
is read as “2.5 meters per second per second” (or “2.5 meters per second squared”) and means that the velocity changes by 2.5 m/s during each second of the motion.