Concepts & Calculations Group Learning Problems

Note: Each of these problems consists of Concept Questions followed by a related quantitative Problem. They are designed for use by students working alone or in small learning groups. The Concept Questions involve little or no mathematics and are intended to stimulate group discussions. They focus on the concepts with which the problems deal. Recognizing the concepts is the essential initial step in any problem-solving technique.

	85

Concept Questions A spring lies on a horizontal table, and the left end is attached to a wall. The other end is connected to a box. The box is pulled to the right, stretching the spring. Static friction exists between the box and the table. When the box is released, it does not move. (a) Is the direction of the restoring force of the spring the same as or opposite to the direction of the static frictional force? Why? (b) How is the magnitude of the restoring force related to the magnitude of the static frictional force? (c) What factors determine the maximum static frictional force that can be applied to the box?

Problem A 0.80-kg box is attached to a horizontal spring whose spring constant is 59 N/m. The coefficient of static friction between the box and the table on which it rests is m_S=0.74. How far can the spring be stretched from its unstrained position without the box moving?

	86

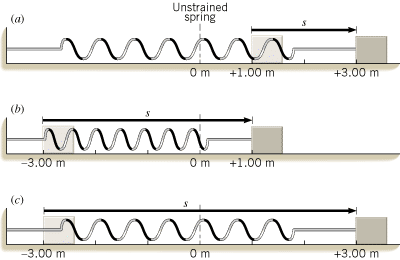
Concept Question The drawing shows three situations in which a block is attached to a spring. The position labeled “0 m” represents the unstrained position of the spring. The block is moved from an initial position x₀ to a final position x_f. The displacement is s. For each case, determine the direction of the restoring force as the block is moved. (Note that the direction of this force may change during the movement.) Then, without doing any calculations, decide whether the total work done by the restoring force of the spring is positive, negative, or zero. Give your reason for each answer in terms of the directions of the displacement and the restoring force.

Problem Suppose the spring constant is k=46.0 N/m. Using the data provided in the drawing, determine the total work done by the restoring force of the spring for each situation. Verify that your answers are consistent with your answers to the Concept Question.

	87

Concept Questions A spring is resting vertically on a table. A small box is dropped onto the top of the spring and compresses it. (a) Two forces are acting on the box: its weight and the restoring force of the spring. What law determines the relationship between these forces when the acceleration of the box is zero? (b) What is the speed of the box when the spring is fully compressed? (c) Many people say that the acceleration of the box is zero when the spring is fully compressed. Is this correct? Explain why or why not.

Problem Suppose the spring has a spring constant of 450 N/m and the box has a mass of 1.5 kg. The speed of the box just before it makes contact with the spring is 0.49 m/s. (a) Determine the magnitude of the spring’s displacement at the instant when the acceleration of the box is zero. (b) What is the magnitude of the spring’s displacement when the spring is fully compressed?

	88

Concept Question The different types of energy possessed by a falling bungee jumper are discussed in Concepts & Calculations Example 15. When the jumper reaches his lowest point in the fall, which is above the water, what types of energy does he have? Provide a reason for each answer.

Problem Using the data given in Concepts & Calculations Example 15, determine how far he is from the water when he reaches the lowest point in the fall.

	89

Concept Questions Two physical pendulums (not simple pendulums) are made from meter sticks that are suspended from the ceiling at one end. They are identical, except that one is made of wood and the other of metal. They are set into oscillation and execute simple harmonic motion. (a) How does the angular frequency of a physical pendulum depend on its mass? Take into account how the mass enters directly as well as indirectly through the moment of inertia. (b) Which pendulum, if either, has the greatest period? Why?

Problem The wood and metal pendulums have masses of 0.17 and 0.85 kg, respectively. Determine the periods of the two physical pendulums. Check to see that your answers are consistent with your answers to the Concept Questions.

	90

Concept Questions One end of a piano wire is wrapped around a cylindrical tuning peg and the other end is fixed in place. The tuning peg is turned so as to stretch the wire. (a) For each turn of the tuning peg, by how much does the length of the wire change? Express your answer in terms of the radius of the tuning peg. (b) As the wire is stretched, do you expect the tension to increase, decrease, or remain the same? Why?

Problem The piano wire is made from steel (Y=2.0× 10¹¹ N/m²). It has a radius of 0.80 mm, and an unstrained length of 0.76 m. The radius of the tuning peg is 1.8 mm. Initially, there is no tension in the wire. Find the tension in the wire when the tuning peg is turned through two revolutions.

	91	*

Concept Questions A vertical ideal spring is mounted on the floor. A block is placed on the unstrained spring in two different ways. (a) The block is placed on the spring and not released until it rests stationary on the spring in its equilibrium position. As the block rests on the spring in equilibrium, what determines how much the spring is compressed? Explain. (b) Immediately after being placed on the unstrained spring, the block is released from rest and falls downward until it comes to a momentary halt. What determines how much the spring is compressed in this case, which is not an example of equilibrium? Account for your answer. (c) In which of the situations described in (a) and (b) is the compression of the spring greater? Give a reason for your answer.

Problem The spring constant of the spring is 170 N/m, and the mass of the block is 0.64 kg. Determine the amount by which the spring is compressed in Concept Questions (a) and (b). Verify that your answers are consistent with your answer to Concept Question (c).

	92	*

Concept Questions Depending on how you fall, you can break a bone easily. The severity of the break depends on how much energy the bone absorbs in the accident, and to evaluate this let us treat the bone as an ideal spring. (a) The applied force needed to change the length of a spring is given by Equation 10.1, where the change is denoted by the displacement x. To change the length of a bone, the necessary applied force is given by Equation 10.17, where the change is denoted by DL rather than x. Recognizing that these two equations are equivalent, explain which factors determine the effective spring constant k of a piece of bone, such as the thighbone (femur) in the leg. (b) The elastic potential energy for an ideal spring is given by Equation 10.13. Using Equation 10.1, discuss how the energy can be expressed in terms of the force applied to the spring. (c) When a person falls from rest from a height and strikes the ground stiff-legged and comes to rest without rotating, what determines the amount of energy that his legs must absorb as elastic potential energy? Justify your answer. You may ignore air resistance and friction.

Problem The maximum applied force of compression that one man’s thighbone can endure without breaking is 7.0×10⁴ N. The minimum effective cross-sectional area of the bone is 4.0×10^–4 m², and its length is 0.55 m. The mass of the man is 65 kg. He falls straight down without rotating, strikes the ground stiff-legged on one foot, and comes to a halt without rotating. To see that it is easy to break a thighbone when falling in this fashion, find the maximum distance through which his center of gravity can fall without his breaking a bone.