In conducting materials such as copper, electric charges move readily in response to the forces that electric fields exert. This property of conducting materials has a major effect on the electric field that can exist within and around them. Suppose that a piece of copper carries a number of excess electrons somewhere within it, as in Figure 18.29a. Each electron would experience a force of repulsion because of the electric field of its neighbors. And, since copper is a conductor, the excess electrons move readily in response to that force. In fact, as a consequence of the 1/r² dependence on distance in Coulomb’s law, they rush to the surface of the copper. Once static equilibrium is established with all of the excess charge on the surface, no further movement of charge occurs, as part b of the drawing indicates. Similarly, excess positive charge also moves to the surface of a conductor. In general, at equilibrium under electrostatic conditions, any excess charge resides on the surface of a conductor.

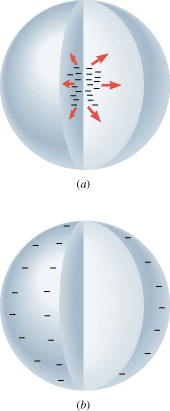Figure 18.29  (a) Excess charge within a conductor (copper) moves quickly (b) to the surface.

Now consider the interior of the copper in Figure 18.29b. The interior is electrically neutral, although there are still free electrons that can move under the influence of an electric field. The absence of a net movement of these free electrons indicates that there is no net electric field present within the conductor. In fact, the excess charges arrange themselves on the conductor surface precisely in the manner needed to make the electric field zero within the material. Thus, at equilibrium under electrostatic conditions, the electric field is zero at any point within a conducting material. This fact has some fascinating implications.

Figure 18.30a shows an uncharged, solid, cylindrical conductor at equilibrium in the central region of a parallel plate capacitor. Induced charges on the surface of the cylinder alter the electric field lines of the capacitor. Since an electric field cannot exist within the conductor under these conditions, the electric field lines do not penetrate the cylinder. Instead, they end or begin on the induced charges. Consequently, a test charge placed inside the conductor would feel no force due to the presence of the charges on the capacitor. In other words, the conductor shields any charge within it from electric fields created outside the conductor. The shielding results from the induced charges on the conductor surface.

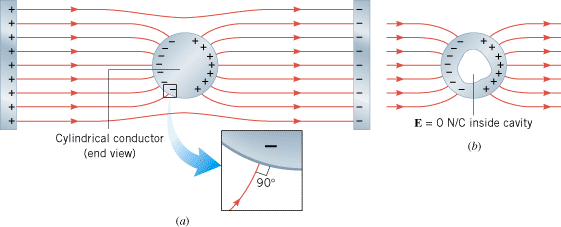Figure 18.30  (a) A cylindrical conductor (shown as an end view) is placed between the oppositely charged plates of a capacitor. The electric field lines do not penetrate the conductor. The blowup shows that, just outside the conductor, the electric field lines are perpendicular to its surface. (b) The electric field is zero in a cavity within the conductor.

Since the electric field is zero inside the conductor, nothing is disturbed if a cavity is cut from the interior of the material, as in part b of the drawing. Thus, the interior of the cavity is also shielded from external electric fields, a fact that has important applications, particularly for shielding electronic circuits. “Stray” electric fields are produced by various electrical appliances (e.g., hair dryers, blenders, and vacuum cleaners), and these fields can interfere with the operation of sensitive electronic circuits, such as those in stereo amplifiers, televisions, and computers. To eliminate such interference, circuits are often enclosed within metal boxes that provide shielding from external fields.

The blowup in Figure 18.30a shows another aspect of how conductors alter the electric field lines created by external charges. The lines are altered because the electric field just outside the surface of a conductor is perpendicular to the surface at equilibrium under electrostatic conditions. If the field were not perpendicular, there would be a component of the field parallel to the surface. Since the free electrons on the surface of the conductor can move, they would do so under the force exerted by that parallel component. In reality, however, no electron flow occurs at equilibrium. Therefore, there can be no parallel component, and the electric field is perpendicular to the surface.

The preceding discussion deals with features of the electric field within and around a conductor at equilibrium under electrostatic conditions. These features are related to the fact that conductors contain mobile free electrons and do not apply to insulators, which contain very few free electrons. Example 13 further explores the behavior of a conducting material in the presence of an electric field.

A charge +q is suspended at the center of a hollow, electrically neutral, spherical conductor, as Figure 18.31 illustrates. Show that this charge induces (a) a charge of –q on the interior surface and (b) a charge of +q on the exterior surface of the conductor. 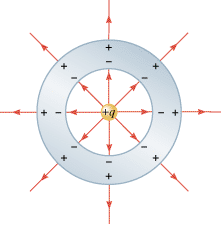Figure 18.31  A positive charge + q is suspended at the center of a hollow spherical conductor that is electrically neutral. Induced charges appear on the inner and outer surfaces of the conductor. The electric field within the conductor itself is zero. Reasoning and Solution (a) Electric field lines emanate from the positive charge +q. Since the electric field inside the metal conductor must be zero at equilibrium under electrostatic conditions, each field line ends when it reaches the conductor, as the picture shows. Since field lines terminate only on negative charges, there must be an induced negative charge on the interior surface of the conductor. Furthermore, the lines begin and end on equal amounts of charge, so the magnitude of the total induced charge is the same as the magnitude of the charge at the center. Thus, the total induced charge on the interior surface is –q. (b) Before the charge +q is introduced, the conductor is electrically neutral. Therefore, it carries no net charge. We have also seen that there can be no excess charge within the metal. Thus, since an induced charge of –q appears on the interior surface, a charge of +q must be induced on the outer surface. The positive charge on the outer surface generates field lines that radiate outward (see the drawing) as if they originated from the central charge and the conductor were absent. The conductor does not shield the outside from the field produced by the charge on the inside. Related Homework: Problem 57

Copyright © 2000-2003 by John Wiley & Sons, Inc. or related companies. All rights reserved.