| 95. |
On earth, two parts of a space probe weigh 11 000 N and 3400 N. These parts are separated by a center-to-center distance of
12 m and may be treated as uniform spherical objects. Find the magnitude of the gravitational force that each part exerts
on the other out in space, far from any other objects.
|
 |
 |
| 96. |
The space probe Deep Space 1 was launched on October 24, 1998. Its mass was 474 kg. The goal of the mission was to test a new kind of engine called an
ion propulsion drive. This engine generated only a weak thrust, but it could do so over long periods of time with the consumption
of only small amounts of fuel. The mission was spectacularly successful. At a thrust of 56 mN how many days were required
for the probe to attain a velocity of 805 m/s (1800 mi/h), assuming that the probe started from rest and that the mass remained
nearly constant?
|
 |
 |
| 97. |
A rocket blasts off from rest and attains a speed of 45 m/s in 15 s. An astronaut has a mass of 57 kg. What is the astronaut's
apparent weight during takeoff?
|
 |
 |
| 98. |
Only two forces act on an object (mass = 3.00 kg), as in the drawing. Find the magnitude and direction (relative to the x axis) of the acceleration of the object.
|
 |
 |
| 99. |
A 60.0-kg crate rests on a level floor at a shipping dock. The coefficients of static and kinetic friction are 0.760 and 0.410,
respectively. What horizontal pushing force is required to (a) just start the crate moving and (b) slide the crate across the dock at a constant speed?
|
 |
 |
| 100. |
Concept Simulation 4.1 reviews the central idea in this problem. A boat has a mass of 6800 kg. Its engines generate a drive force of 4100 N due
west, while the wind exerts a force of 800 N due east and the water exerts a resistive force of 1200 N due east. What is the
magnitude and direction of the boat's acceleration?
|
 |
 |
| 101. |
A 1.14 × 104-kg lunar landing craft is about to touch down on the surface of the moon, where the acceleration due to gravity is 1.60 m/s2. At an altitude of 165 m the craft's downward velocity is 18.0 m/s. To slow down the craft, a retrorocket is firing to provide
an upward thrust. Assuming the descent is vertical, find the magnitude of the thrust needed to reduce the velocity to zero
at the instant when the craft touches the lunar surface.
|
 |
 |
| 102. |
A woman stands on a scale in a moving elevator. Her mass is 60.0 kg, and the combined mass of the elevator and scale is an
additional 815 kg. Starting from rest, the elevator accelerates upward. During the acceleration, the hoisting cable applies
a force of 9410 N. What does the scale read during the acceleration?
|
 |
 |
| 103. |
A 15-g bullet is fired from a rifle. It takes 2.50 × 10-3 s for the bullet to travel the length of the barrel, and it exits the barrel with a speed of 715 m/s. Assuming that the acceleration
of the bullet is constant, find the average net force exerted on the bullet.
|
 |
 |
| 104. |
A person in a kayak starts paddling, and it accelerates from 0 to 0.60 m/s in a distance of 0.41 m. If the combined mass of
the person and the kayak is 73 kg, what is the magnitude of the net force acting on the kayak?
|
 |
 |
| 105. |
Mars has a mass of 6.46 × 1023 kg and a radius of 3.39 × 106 m. (a) What is the acceleration due to gravity on Mars? (b) How much would a 65-kg person weigh on this planet?
|
 |
 |
| 106. |
The drawing shows three particles far away from any other objects and located on a straight line. The masses of these particles
are mA = 363 kg, mB = 517 kg, and mC = 154 kg. Find the magnitude and direction of the net gravitational force acting on (a) particle A, (b) particle B, and (c) particle C.
|
 |
 |
| *107. |
Two objects (45.0 and 21.0 kg) are connected by a massless string that passes over a massless, frictionless pulley. The pulley
hangs from the ceiling. Find (a) the acceleration of the objects and (b) the tension in the string.
|
 |
 |
| *108. |
The central ideas in this problem are reviewed in Multiple-Concept Example 9. One block rests upon a horizontal surface. A second identical block rests upon the first one. The coefficient of static
friction between the blocks is the same as the coefficient of static friction between the lower block and the horizontal surface.
A horizontal force is applied to the upper block, and the magnitude of the force is slowly increased. When the force reaches
47.0 N, the upper block just begins to slide. The force is then removed from the upper block, and the blocks are returned
to their original configuration. What is the magnitude of the horizontal force that should be applied to the lower block so
that it just begins to slide out from under the upper block?
|
 |
 |
| *109. |
A skier is pulled up a slope at a constant velocity by a tow bar. The slope is inclined at 25.0° with respect to the horizontal.
The force applied to the skier by the tow bar is parallel to the slope. The skier's mass is 55.0 kg, and the coefficient of
kinetic friction between the skis and the snow is 0.120. Find the magnitude of the force that the tow bar exerts on the skier.
|
 |
 |
| *110. |
Interactive LearningWare 4.3 reviews the principles that play a role in this problem. During a storm, a tree limb breaks off and comes to rest across
a barbed wire fence at a point that is not in the middle between two fence posts. The limb exerts a downward force of 151
N on the wire. The left section of the wire makes an angle of 14.0° relative to the horizontal and sustains a tension of 447
N. Find the magnitude and direction of the tension that the right section of the wire sustains.
|
 |
 |
| *111. |
A person whose weight is 5.20 × 102 N is being pulled up vertically by a rope from the bottom of a cave that is 35.1 m deep. The maximum tension that the rope
can withstand without breaking is 569 N. What is the shortest time, starting from rest, in which the person can be brought
out of the cave?
|
 |
 |
| *112. |
Refer to Concept Simulation 4.4 for background relating to this problem. The drawing shows a large cube (mass = 25 kg) being accelerated across a horizontal
frictionless surface by a horizontal force 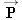 . A small cube (mass = 4.0 kg) is in contact with the front surface of the large cube and will slide downward unless 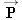 is sufficiently large. The coefficient of static friction between the cubes is 0.71. What is the smallest magnitude that
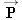 can have in order to keep the small cube from sliding downward?
|
 |
 |
| *113. |
A space probe has two engines. Each generates the same amount of force when fired, and the directions of these forces can
be independently adjusted. When the engines are fired simultaneously and each applies its force in the same direction, the
probe, starting from rest, takes 28 s to travel a certain distance. How long does it take to travel the same distance, again
starting from rest, if the engines are fired simultaneously and the forces that they apply to the probe are perpendicular?
|
 |
 |
| *114. |
A spacecraft is on a journey to the moon. At what point, as measured from the center of the earth, does the gravitational
force exerted on the spacecraft by the earth balance that exerted by the moon? This point lies on a line between the centers
of the earth and the moon. The distance between the earth and the moon is 3.85 × 108 m, and the mass of the earth is 81.4 times as great as that of the moon.
|
 |
 |
| *115. |
A person is trying to judge whether a picture (mass = 1.10 kg) is properly positioned by temporarily pressing it against a
wall. The pressing force is perpendicular to the wall. The coefficient of static friction between the picture and the wall
is 0.660. What is the minimum amount of pressing force that must be used?
|
 |
 |
| **116. |
As part a of the drawing shows, two blocks are connected by a rope that passes over a set of pulleys. One block has a weight of 412
N, and the other has a weight of 908 N. The rope and the pulleys are massless and there is no friction. (a) What is the acceleration of the lighter block? (b) Suppose that the heavier block is removed, and a downward force of 908 N is provided by someone pulling on the rope, as part
b of the drawing shows. Find the acceleration of the remaining block. (c) Explain why the answers in (a) and (b) are different.
|
 |
 |
| **117. |
A penguin slides at a constant velocity of 1.4 m/s down an icy incline. The incline slopes above the horizontal at an angle
of 6.9°. At the bottom of the incline, the penguin slides onto a horizontal patch of ice. The coefficient of kinetic friction
between the penguin and the ice is the same for the incline as for the horizontal patch. How much time is required for the
penguin to slide to a halt after entering the horizontal patch of ice?
|
 |
 |
| *118. |
The basic concepts in this problem are presented in Multiple-Concept Example 9. A 225-kg crate rests on a surface that is inclined above the horizontal at an angle of 20.0°. A horizontal force (magnitude
= 535 N and parallel to the ground, not the incline) is required to start the crate moving down the incline. What is the coefficient
of static friction between the crate and the incline?
|
 |
 |
| *119. |
While moving in, a new homeowner is pushing a box across the floor at a constant velocity. The coefficient of kinetic friction
between the box and the floor is 0.41. The pushing force is directed downward at an angle θ below the horizontal. When θ is
greater than a certain value, it is not possible to move the box, no matter how large the pushing force is. Find that value
of θ.
|
 |
 |
|