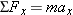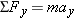When a football player throws a pass, the direction of the force he applies to the ball is important. Both the force and the
resulting acceleration of the ball are vector quantities, as are all forces and accelerations. The directions of these vectors
can be taken into account in two dimensions by using
x and
y components. The net force
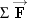
in Newton's second law has components Σ
Fx and Σ
Fy, while the acceleration
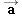
has components
ax and
ay. Consequently, Newton's second law, as expressed in Equation
4.1, can be written in an equivalent form as two equations, one for the
x components and one for the
y components:
This procedure is similar to that employed in Chapter
3 for the equations of two-dimensional kinematics (see Table 3.1). The components in Equations
4.2a and
4.2b are scalar components and will be either positive or negative numbers, depending on whether they point along the positive
or negative
x or
y axis. The remainder of this section deals with examples that show how these equations are used.
 |
 |
 |
Example 2 Applying Newton's Second Law Using Components |
|
 |
 |
 |
 |
|
A man is stranded on a raft (mass of man and raft = 1300 kg), as shown in Figure 4.6a. By paddling, he causes an average force 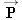 of 17 N to be applied to the raft in a direction due east (the + x direction). The wind also exerts a force 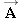 on the raft. This force has a magnitude of 15 N and points 67° north of east. Ignoring any resistance from the water, find
the x and y components of the raft's acceleration.
 |
 |
|
|
 |

|
Figure 4.6 |
 |
|
(a)
|
A man is paddling a raft, as in Examples 2 and 3.
|
 |
|
(b)
|
The free-body diagram shows the forces 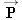 and 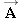 that act on the raft. Forces acting on the raft in a direction perpendicular to the surface of the water play no role in
the examples and are omitted for clarity.
|
 |
|
(c)
|
The raft's acceleration components ax and ay.
|
 |
|
(d)
|
In 65 s, the components of the raft's displacement are x = 48 m and y = 23 m.
|
|
|
|
 |
|
 |
 |
|
|
 |
|
Applications of Newton's second law always involve the net external force, which is the vector sum of all the external forces
that act on an object. Each component of the net force leads to a corresponding component of the acceleration.
|
|
|
Reasoning
Since the mass of the man and the raft is known, Newton's second law can be used to determine the acceleration components
from the given forces. According to the form of the second law in Equations 4.2a and 4.2b, the acceleration component in a given direction is the component of the net force in that direction divided by the mass.
As an aid in determining the components ΣFx and ΣFy of the net force, we use the free-body diagram in Figure 4.6b. In this diagram, the directions due east and due north are the +x and +y directions, respectively.
Solution
Figure 4.6b shows the force components:
 |
 |
|
Force
|
x Component
|
y Component
|
|
|
+17 N
|
0 N
|
|
|
+(15 N) cos 67° = +6 N
|
+(15 N) sin 67° = +14 N
|
| |
|
|
|
|
|
|
 |
|
 |
The plus signs indicate that Σ Fx points in the direction of the + x axis and Σ Fy points in the direction of the + y axis. The x and y components of the acceleration point in the directions of Σ Fx and Σ Fy, respectively, and can now be calculated:
These acceleration components are shown in Figure 4.6c.
|
 |
 |
|
 |
 |
|
 |
 |
 |
 |
 |
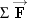 in Newton's second law has components ΣFx and ΣFy, while the acceleration
in Newton's second law has components ΣFx and ΣFy, while the acceleration 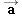 has components ax and ay. Consequently, Newton's second law, as expressed in Equation 4.1, can be written in an equivalent form as two equations, one for the x components and one for the y components:
has components ax and ay. Consequently, Newton's second law, as expressed in Equation 4.1, can be written in an equivalent form as two equations, one for the x components and one for the y components: