Acceleration, Free Fall, Symmetry
Purpose
-
•Observe an accelerating object and draw position vs. time (x-t ), velocity vs. time (v-t ), and acceleration vs. time (a-t ) graphs of its motion.
-
•From an x-t, v-t, or a-t graph of an object with constant acceleration, describe the object's motion.
-
•From an x-t, v-t, or a-t graph of an object with constant acceleration, draw, within limits, the other two graphs.
-
•Analyze video frames to determine the acceleration of an object in free fall.
-
•Investigate symmetries in the motion of an object with constant acceleration.
Equipment
- Dynamics Track simulation
- VPL Grapher
- Pencil
- Frame Flipper tool and video clips of vertical motion
Simulation and Tools
Open the Dynamics Track simulation to do this lab. You will need to use the VPL Grapher to complete this lab.Discussion
In our constant velocity lab, we used the motion sensor to measure the position of an object 100 times a second and plotted the data as a graph of position vs. time. With our Grapher tool, we were able to use our (t, x) data to calculate the rate of change in position and plot this to create a v-t graph. We could then work our way backward to calculate displacements by calculating the area under the v-t graph. The following table summarizes these results as well as some to come in this lab.![Three column table with header row: Graph; Slope; Area. First row is Position-time, x-t; velocity; [dashed line]. Second row is: Velocity-time, v-t; [blank]; displacement, Detla x. Last row is Acceleration-time, a-t; jerk, jolt, surge, lurch; change in velocity, Delta v.](images/image3-1.png)
1
We've also learned the following.
-
aA straight-line position-time graph indicates a velocity.
-
bA straight-line, horizontal position-time graph indicates a velocity.
-
cA steep position-time graph indicates a relatively velocity.
2
We now turn our attention to acceleration. We'll look at position, velocity, and acceleration graphs. The table reminds us that the slope of the position-time graph is the velocity. The slope of the acceleration-time graph and the area under a position-time graph are not of interest to us in this course.
In the table, fill in the name that we give to the slope of the velocity-time graph.
You now have a complete list of the two slopes and two areas that you need to know about
Procedure
Please print the worksheet for this lab. You will need this sheet to record your data.I. Motion on an Incline
A. Position on an Incline
We want to observe the motion of the cart moving freely up the ramp and then back down.1
Start up the Dynamics Track simulation.
Caution:
Don't turn on the motion sensor until you're instructed to.
Don't turn on the motion sensor until you're instructed to.
2
Your low-friction track has a feature that you may not have noticed. If you move your mouse over the small orange rectangle near either end of the track, your pointer changes, and the message box informs you that you can tilt the track by dragging up or down. Give it a try. It's also important to realize that the x-axis rotates with the track.
Setting the track angle can be tricky. Try to set the angle at 3.1°, then 3.2°, then 3.3°. It's not so easy. Try this: Click on the left handle, and with the button still down, drag toward the center of the track. Try setting the angle to 3.2° now. It's nearly impossible. Now try the same, but drag away from the center of the track. Much easier. Think about how that might work.
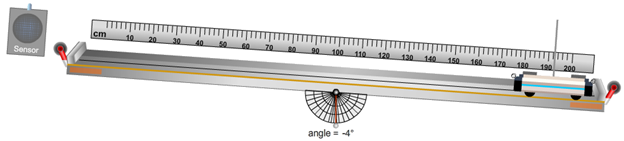
Figure 1: Motion sensor, cart, and track in the Dynamics Track simulation
Adjust your track to an angle between –2° and –6°. Record your chosen track angle.
3
Set "Recoil"
4
Use the "Vo" and Go tools with a negative velocity to find an initial velocity that will send the cart to about the 20-cm point before returning back to the bottom. Remember, the cart's location is defined as the location of its mast. Record your chosen initial velocity, Vo.

Figure 2: Sample negative Vo
Your goal in this lab is to learn to observe an accelerated motion and draw the x-t, v-t, and a-t graphs describing that motion. The three graphs won't look at all alike. You might say they use the same vocabulary, but the words have different meanings. The slope of an x-t graph means something entirely different than the slope of a v-t or an a-t graph. You'll be asked several times to draw your prediction of what a given graph will look like. Then you'll use the apparatus or graphing software to check your work. It doesn't matter so much if your prediction is correct or incorrect. What's important is that you have a clearly reasoned prediction that you can check against your experimental results. That's where the learning happens.
5
Launch your cart a few times (no sensor!) and think about what you'd expect for the shape of an x-t graph of this motion—starting at the bottom, up to near the top, and then back to the bottom of the ramp.
Let's do some hand drawing on Graph IA1a. You'll (later) start the sensor and, hence, the graph, and then wait about two seconds before launching the cart. So the x-t graph will indicate a stationary cart for maybe 2 seconds. From your velocity graphing lab, you know that this would produce a horizontal line on an x-t graph. But where? The cart is initially at its lowest point. Does that correspond to a low position value on the graph, like 10 cm? Look at the ruler.
Approximately, what is the starting position, xo, of the cart?
6
Draw a dot at approximately (to = 0 s, xo), showing where the cart is initially. Draw another dot at (t = 2 s, xo), just before launch. Draw another pair of dots for the at-rest period after it returns to the bottom, maybe at 8 and 10 seconds. Draw a horizontal line between the first two dots and another between the second two dots. OK, the accelerated motion that we're interested in is just from the "2-second" point to the "8-second" point. So erase the two lines and the first and last dots. They were used just to get you oriented on the graph. Also, the exact times of 2 and 8 seconds are not important. They depend on your track angle and initial velocity. Right now we're only interested in the shape of the graph.
7
The cart will only be at the top of the track at an instant, say, at t top = 5 s. Launch the cart a few times to get a reasonable value for the position, xtop, when the cart is at the top of the track.
Approximately, what is xtop?
Put one dot at (t top = 5 s, xtop).
8
Drawing lightly with your pencil, connect the points at 2 and 5 seconds with a straight line. Repeat for the points at 5 and 8 seconds. You should now have a nice, symmetrical V. The slopes of the two lines would indicate two periods of constant velocity. Is that correct? No, the speed actually smoothly changes over time, so the slope should also smoothly change. It should be steep when the speed is large and horizontal when the cart is not moving. And it should never be vertical. What about the signs of the slopes? You learned about that in the velocity lab, too. Add a smooth curve with a slope that changes to match this pattern. Erase the V.
9
For each of the following, describe the motion of the cart and the related shape of your graph. You should use words like rise, fall, slow, fast, slowing down, speeding up, positive direction, negative direction, steep, and ±slope.
-
afor the trip up the ramp
-
bwhen the cart is at the top of the ramp
-
cfor the trip back down the ramp
10
Use the Sketch Graph
Graph IA: Position on an incline prediction and observation
11
Now try it with the detector on. Sweet! Draw the observed x-t graph in Graph IA1b. (Omit the constant velocity periods.)
12
Copy your data to Grapher as follows.
-
aIn the Dynamics Track simulation, click Copy Data to Clipboard.
-
bOpen Grapher and turn on just Graph "1" (check box).
-
cClick in the box below the data table and hit Ctrl+V to paste data.
-
dTurn on "Titles" (check box). In the text field provided, add an appropriate title—"Position (m) vs. time (s)".
13
Before we move on, note the obvious symmetry in the cart's motion. The trip up the ramp is replayed in reverse on the way back down. The graph is also symmetrical about a line passing through the maximum position. We'll return to this shortly.
B. Velocity on an Incline
We now want to consider a graph of velocity vs. time for the cart's motion up and back down the track. What would that look like? As usual, a concise conversation with your lab partner would be a good idea.1
The cart starts off traveling in a negative direction. Describe the cart's motion in terms of its changing velocity. Be sure to include the direction of the velocity, which at a given instant will be negative, positive, or neither. Also include the magnitude, which will be large when the cart is going fast, small when it's going slowly, and zero when it's at rest.
2
Based on your description, draw your prediction of the shape of the velocity-time graph you'd expect in Graph IB1a. Note: Take some time to think about this. Most students miss this one entirely. It might be good to consider the cart's velocity at several instants and plot points on the graph to match. Then think about the shape that would connect them.
Graph IB: Velocity on an incline prediction and observation
3
Use Sketch Graph to create a sketch of your prediction. Take a Screenshot and upload it as "Accel_IB1a.png".
4
In Grapher, add Graph "2" and click the Graphs button to choose a Y' ("Y prime") graph. Y' is an abbreviation for the derivative of value on the y-axis with respect to the value on the x-axis. So in this case, it's the derivative of the position, x, with respect to time, t, which is the slope of the x-t graph and, thus, the cart's velocity.
5
You now have a v-t graph. Add an appropriate title, including units.
You may need to adjust the maximum and minimum values of the velocity axis so that the interval where it was freely moving almost fills the graph vertically (e.g., –2 m/s to +2 m/s). To do this, click the Manu button beside the v-t graph. The settings shown in Figure 3 should work pretty well. Draw your observed graph in Graph IB1b.
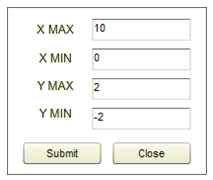
Figure 3: Manual scaling tool in the Dynamics Track simulation
6
Any surprises? It seems like the v-t graph should change when the cart gets to the top of the ramp, but instead it just keeps on rising. What about the v-t graph does change when the cart reaches the top?
7
Look at your graph and your prediction for the velocity vs. time graph. It's very important that your words say the same thing as the graph. It's also important that you convince yourself that the graph makes sense. Feel free to change your answer to your prediction.
8
Clearly describe your v-t graph (not the motion!). You should know the details we're looking for now.
This mangled bit of literature may help you prepare for the next question:
- Once upon a time a moocow went down the road for four hours. It arrived at the home of baby tuckoo at three o'clock in the afternoon.
9
Consider the cart at the highest point it reaches along the track. Its velocity there is zero. Does it have this velocity of zero for an instant or at an instant at the top of its motion? Choose one of these two and explain your answer. (Look at your graph!)
C. Acceleration on an Incline
1
Look back at the table in the Discussion. How do we find acceleration from a velocity-time graph?
2
Based on that answer, you should be able to look at your v-t graph and predict the shape of the corresponding a-t graph.
-
aDraw your prediction of the shape of the cart's a-t graph in Graph IC1a.
-
bUse Sketch Graph to create a sketch of your prediction.
-
cTake a Screenshot and upload it as "Accel_IC1a.png".
3
Now use Grapher to create the acceleration-time graph. It will do this by taking the derivative of the velocity with respect to time. Remember, we found that the term "derivative" refers to the rate of change of some quantity. The derivative of the position with respect to the time is the velocity. The derivative of the velocity with respect to time is acceleration. You'll need to add Graph "3" and set it to Y'' to display the acceleration.
4
Draw Grapher's graph in Graph IC1b.
Graph IC: Acceleration on an incline prediction and observation
5
Take a Screenshot of all three graphs. Upload it as "Accel_rampGraphs.png" to document your results.
6
You may have been surprised by what you saw. Shouldn't the acceleration be somehow different going up than going down, just like we saw with velocity? This is what was meant by the earlier remark, "You might say they use the same vocabulary, but the words have different meanings." The cart's constantly changing velocity is indicated by a constantly changing slope on an x-t graph, a constant slope on a v-t graph, and a constant value on an a-t graph!
-
•The sign of the position indicates the location of an object relative to the zero point.
-
•The sign of the velocity indicates the direction of motion toward the positive or negative end of the axis.
-
•The sign of the acceleration indicates the direction of the change in velocity, Δv.
-
•During the 1st second, it changes from –2.0 m/s, by +1.0 m/s, to –1.0 m/s. It's slowing down in the – direction.
-
•During the 2nd second, it changes from –1.0 m/s, by +1.0 m/s, to 0.0 m/s. It's slowing down in the – direction.
-
•During the 3rd second, it changes from 0.0 m/s, by +1.0 m/s, to +1.0 m/s. It's speeding up in the + direction.
-
•During the 4th second, it changes from +1.0 m/s, by +1.0 m/s, to +2.0 m/s. It's speeding up in the + direction.
A constant velocity means that something changes its position at a constant rate.
A constant acceleration means that something changes its velocity at a constant rate.
If the acceleration is in the opposite direction of something's motion, it will slow down, and may also change direction.
-
•When an object is speeding up, its velocity and acceleration have the same signs.
-
•When an object is slowing down, its velocity and acceleration have opposite signs.
7
The Dynamic Vectors
8
Launch the cart with the same ramp angle and initial velocity that you've been using throughout the lab. The green vector arrow represents the velocity. Notice how it continues to change in magnitude and eventually direction, starting from full length, going up the ramp to zero length, and then pointing down the ramp and increasing in length.
It's a good exercise to think about how each graph, x-t, v-t, and a-t, predicts how this vector changes in magnitude and direction.
The black arrow represents both the total force on the cart and its acceleration. We'll discuss these forces soon, but for now, just notice the acceleration. It's constant and always directed down the ramp. Now look at the two bulleted statements above. Hopefully, you can "see" what they're saying now.
-
aWhen the cart is rolling up the ramp, its velocity is negative since it's moving in the negative direction. And the cart is slowing down. What is the sign of its acceleration?
-
bWhen the cart is rolling down the ramp, its velocity is positive since it's moving in the positive direction. And it's speeding up. What is the sign of its acceleration?
9
You now have two graphs that can provide values for the acceleration of the cart. The acceleration-time graph has a varying height that clearly varies around a certain average value during the period of constant acceleration. Select this part of the graph by dragging across it. Click the "Stats" check box to find the average (mean) value of the acceleration. Record your results.
(The extra wiggle in the acceleration graph is due to a bug in our apparatus. If you search the data at that point, you'll see that the cart has an unchanging position for two or more time readings at the top of the motion. Sorry.)
10
Another way of determining the acceleration is from the slope of the line of best fit of the velocity graph. Drag across the velocity graph where the acceleration (slope) is constant and click the "Linear Fit" check box. The slope is the acceleration. Record your results.
D. Find the Acceleration Due to Gravity, g, from the Acceleration of Our Cart on an Incline
When Galileo studied acceleration along a ramp, he saw that the acceleration increased with the angle of the ramp. He wasn't able to test his measurements given the limitations of using a water clock to measure time, but he did predict that some maximum acceleration would be reached when the ramp was tilted to 90°. We refer to this vertical acceleration of a freely falling object as the acceleration due to gravity, g. Later in the course, we'll show that g should equal a/tan(θ), where a is the acceleration for some ramp angle, θ.1
Let's see what your results would predict for g. Determine the predicted maximum acceleration, aavg/tan(θ), using the average of your two acceleration values.
2
Compare this result to the value assumed in the lab, 9.80 m/s2, by finding the percentage error.
E. The Area Under an Acceleration vs. Time Graph
We've now thoroughly studied everything in the table from the Discussion except the area under an a-t graph. The height of the graph is acceleration; the width is Δt. The area is the product of these two. This is best understood from the definition of acceleration. Rearranging, we get So the area, aΔt, is just the change in velocity over the interval Δt. Let's find Δv from vf – vo and from aΔt for the full trip up and back and compare. Let's find everything from our graphs.1
First, the a-t graph: Click in that graph.
Turn on the "Examine" tool and move your cursor over the left-most point on the part of the a-t graph where the cart was actually in motion—the plateau region. (You can move your cursor anywhere above or below this point.)
In the "Examine" box, you'll see the time and acceleration (t, a) for that point. Doing the same with the right-most point, you'll find your final time and acceleration for the trip. Record these values.
2
We could calculate aΔt from this data, but the acceleration actually varies a lot. A better way of getting aΔt is to find the area under the a-t graph.
We'll use the "Integrate" tool, which calculates the area under the graph, taking into account all the variation. Click its check box to turn it on. You want to click and drag across the a-t graph from to to t f. Zooming helps, so right click somewhere near the center of the a-t graph. Click "Zoom In" once. As you move your pointer, a vertical line will move with it. When it is passing through the first xo, and you see a circle around that point, click and start to drag right. When the circle is around the last point on the plateau, release the mouse. Right click and turn off zoom.
The area will be listed in the "Integrate" box. Its units are m/s. Record this value, Δv = area under the a-t graph.
If you need to try again, be sure to turn off "Integrate" until you've selected the area you need.
3
Now read vo and vf from the v-t graph. One problem: It has one extra data point on each end due to the way that the acceleration values are calculated. You've recorded to and t f above, so you can use this to check that you're working with the right points.
4
Compare your two values for Δv by calculating the percentage difference.
II. Free Fall
With our more modern equipment, we can find the acceleration due to gravity, g, without using the ramp to slow down the motion. And we can observe some interesting symmetries found when objects move with constant acceleration. We'll be leaving the Dynamics Track now to work with a video of a billiard ball tossed upward. We'll use a software tool that we call the Frame Flipper. The coding for this tool was written in 1996 by Joe Pearson. He went on to become Application Architect at The Weather Channel. Cool, I think. In your browser, navigate to the video clips of the vertical ball toss. The QuickTime movies in the first two frames may take a while to load. It may help to click in each of these two frames.A Dropped Object
1
In the first column, you'll see a QuickTime movie of a dropped billiard ball that falls through a distance of about 2 meters. Click the Play
2
Briefly describe what you observe in this movie. Use physics lingo!
An Object Thrown Upward
1
Now play the movie of the object thrown upward. This time you'll see the very smooth motion of a billiard ball thrown upward and then allowed to fall back down.
2
How does the trip upward compare to the trip downward in this movie?
3
Notice how the spacing between the images and the fuzziness of the images varies as the ball rises and falls. What do these two observations indicate about the ball's motion? (There are two answers.)
4
Hopefully, you noticed that this second up-and-down motion is just like our ramp investigation. There's one minor but important difference. With our ramp, the ball moved first in a negative direction, then in a positive direction. In this case, the ball will travel in the positive, upward direction, then in the negative, downward direction. We're going to do a quick repeat of the ramp investigation, this time with the billiard ball. Using what you've learned so far, you should be able to draw predictions for all three graphs.
Sketch your graphs, including the axes. Assume the upward direction is positive.
Graph II1: Free fall predictions
5
What will be the sign of the acceleration in this movie, + or –?
6
OK, let's try the actual Frame Flipper (FF). Click the "Frame Flipper" link next to the movies to start it. It will open up a new window. You'll recognize the image as the first frame of the second movie. In this frame, the ball has just been set into motion. That is, it has just been released and is moving only under the influence of gravity and a negligible amount of air resistance. FF allows you to take position vs. time data of a moving object by clicking on it at each successive position. We'll be interested in the vertical position only, so ignore the x-values.
7
In order to get actual measurements in meters, we need to determine the scale of the image, that is, determine how many pixels tall our meter stick in the figure is. (Do Steps 1 and 2.) We then need to set the y = 0.0 m point. (Do Step 3.) Then we can start taking our data (Step 4, which repeats). You should be able to work this out by reading the directions on the screen. FF will automatically advance from Step 1 to Step 2 to Step 3 to Step 4 when you click on the screen. You'll repeat Step 4 for as many frames as the ball takes to rise and fall (38), clicking the forward arrow each time to advance the movie. If you make an error, you can close the window and re-open it. Go ahead and collect all your data. It's a bit blurry, so take care.
8
To copy and paste your t and y data from FF to Grapher, you just need to copy the y-column. The time data will come along with it. In FF, click anywhere in the y(m)-column. Right click and choose "Select All," then right click and select "Copy." Open Grapher and paste (Ctrl+V) your data into the table. Scale your graphs as needed. You should have a nice down-opening parabola and its associated v-t and a-t graphs. (Hopefully, that's what you predicted.)
9
In Graph II2, draw the three graphs produced by Grapher.
Note:
Graph II2c is very wiggly due to imprecision of Frame Flipper data. You might also note that a small "oops" in the x-t graph will produce a couple of bad velocity points and about twice as many bad a-t points. This is a nice visual representation of what's called propagation of error. An error in one point in the x-t graph affects the calculation of the velocity in the two time intervals on either side of it. Similarly, the problem is compounded with the acceleration calculations.
Graph II2c is very wiggly due to imprecision of Frame Flipper data. You might also note that a small "oops" in the x-t graph will produce a couple of bad velocity points and about twice as many bad a-t points. This is a nice visual representation of what's called propagation of error. An error in one point in the x-t graph affects the calculation of the velocity in the two time intervals on either side of it. Similarly, the problem is compounded with the acceleration calculations.
Graph II2: Free fall observations
10
From the movie, we can see that the ball is at rest (v = 0) at the top of its motion. How do the y-t and v-t graphs indicate this?
11
Does this mean that its acceleration is zero there? How do the v-t and a-t (sort of) graphs answer this?
What we've found is that, in the absence of friction, vertical motion is motion at a constant acceleration. Note that the term vertical motion applies to either upward or downward motion. The magnitude of the acceleration due to gravity, g, varies from location to location, but a typical value is 9.80 m/s2. Its direction is always downward.
12
You can probably get your best experimental value for this acceleration from the slope of your v-t graph. Record this.
13
Compare your experimental value to the accepted value by finding the percentage error between your experimental value and our accepted value.
III. Observations of Symmetry
1
We noted earlier that the x-t graph was symmetrical. But we've also stated that these graphs model the motions we observe. What symmetries should we find in our models and our motions?
How does an object's acceleration while rising compare to its acceleration while falling? Explain your answer using either the v-t graph or the a-t graph.
2
With this information and our kinematics equations, we can solve problems with vertical motion. There are a couple of useful observations we can make from our data that will help with problem solving.
Using Grapher, turn on "Examine" and "Tangent." As you move your pointer across the x-t graph, a short tangent line will follow your cursor, and the tangent at the nearest data point will display in the tangent text box. In the "Examine" box, you'll see (time-position) values constantly updated. For some position, y, on the left (ball rising) side of the graph, note the slope. Now repeat for the same position, y, on the right (ball falling) side of the graph. (You won't be able to get identical heights. Just get close.) The magnitude of the slope is the speed. How do speeds compare at corresponding heights? Repeat for another pair of matching heights. State your observations.
3
As you move your pointer across the position-time graph, the time to reach each y-position found in your data table appears in a box.
-
aUsing this tool, find the time the ball took to rise between a point near y = 0.5 m and y = 1.5 m.
-
bFind the approximate time between the same positions on the way back down.
-
cPick another similar pair and repeat. (Again, this will just be approximate.)
-
dState your observations.

