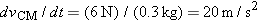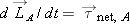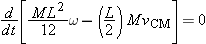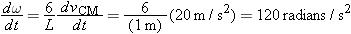Systems with Nonzero Torques

In the remainder of this chapter we will analyze systems in which there are external torques applied to the system, which can change the angular momentum of the system.

example

A Meter Stick on the Ice

Consider a meter stick whose mass is 300 grams and that lies on ice (in Figure 11.50 we're looking down on the meter stick). You pull at one end of the meter stick, at right angles to the stick, with a force of 6 newtons. Assume that friction with the ice is negligible. What is the rate of change of the center-of-mass speed v_CM? What is the rate of change of the angular speed ω?

Figure 11.50

Pull one end of a meter stick that is lying on ice (negligible friction).

Solution

System: Stick

Surroundings: Your hand (pulling); ice (negligible effect)

Momentum Principle:

Angular Momentum Principle about center of mass:

Component into page (−z direction):

In vector terms,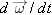

points into the page, corresponding to the fact that the angular velocity points into the page and is increasing.

In Chapter 9 we showed that the moment of inertia I around the center of mass of a uniform rod of mass M and length L is ML²/12; L = 1 m here.

It is interesting to re-analyze the motion of the meter stick by calculating torque and angular momentum about the end of the stick where the force is applied (location A in Figure 11.51), rather than about the center of mass. To be cautious and correct, we should say that we are taking torques about a location fixed in the ice next to the place where the end of the stick is momentarily located. This is a fixed location, not tied to the moving stick.

Figure 11.51

Pull one end of a meter stick that is lying on ice (negligible friction).

There is zero torque about location A, because there is zero distance from A to where the force is applied.

Surroundings: Your hand (pulling); ice (negligible effect)

Momentum Principle unchanged, which gives this:

Angular Momentum Principle about location A:

Component into page (−z direction):

This agrees with our analysis where we took torques about the center of mass of the stick, but the details of the calculation are rather different. It is a good check on an analysis involving the Angular Momentum Principle to do the problem for two different choices of the location about which to calculate the net torque.

Wrap a string around the outside of a hockey puck. Then pull on the string with a constant tension F_T (Figure 11.52). The puck has mass M and radius R. Assume that friction with the ice rink is negligible. Evidently dv_CM/dt = F_T/M.

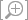
Figure 11.52

Wrap a string around a hockey puck, then pull it along the ice with negligible friction, with a constant tension F_T.

question

	The moment of inertia of a uniform solid puck of mass M and radius R is MR²/2. What is the initial rate of change dω/dt of the angular speed ω?

The torque about the center of mass is RF_T, into the page (down into the ice).

The rotational angular momentum is (MR²/2)ω, into the page (down into the ice). Therefore (MR²/2)dω/dt = RF_T, and we have dω/dt = (2F_T)/(MR).

Redo the analysis, calculating torque and angular momentum relative to a fixed location in the ice anywhere underneath the string (similar to the analysis of the meter stick around one end). Show that the two analyses of the puck are consistent with each other.

If the net torque on a system is zero, its angular momentum is constant. Conversely, if we know that the angular momentum is not changing, we can conclude that the net torque must be zero. For example, if a system is in equilibrium, not only must the net force on the system be zero; the net torque must also be zero. This allows us to make conclusions about the individual torques whose vector sum is zero.

example

Two People on a Seesaw

Figure 11.53 shows two persons on a seesaw. The person on the left has mass M₁ = 90 kg and sits at a distance d₁ = 1.2 m from the nearly frictionless axle. The person on the right has mass M₂ = 40 kg. What is the upward force that the axle must exert? Where must the person on the right sit in order that the seesaw not rotate? The seesaw itself has negligible mass.

Figure 11.53

A seesaw in equilibrium.

Solution

System: The two persons and the seesaw

Surroundings: Earth and axle

Principle: The Momentum Principle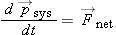

Since the system is not moving, the momentum of the system isn't changing, so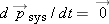

, and therefore the net force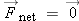

. Consider the y forces:

It isn't surprising to find that the axle must exert an upward force equal to the combined weights of the two persons. Next we use a different principle to determine where the person on the right should sit.

Principle: The Angular Momentum Principle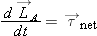

Since the angular momentum isn't changing,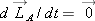

about any point whatsoever, and therefore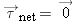

about any point whatsoever. It is convenient to choose point A to be at the location of the axle, because then the upward force of the axle exerts no torque about point A. Consider the z component of the net torque:

This analysis would also be valid if the seesaw were rotating at a constant angular velocity, because it would still be the case that the angular momentum would not be changing, and the net torque would be zero.

This is an example of a category of “statics” problems in which it is necessary to consider both the Momentum Principle and the Angular Momentum Principle in order to carry out a complete analysis.

Write a different torque equation around a location fixed in space where the person on the left is sitting, and show that it is in fact equivalent to the torque equation around the axle, when you take the force equation into consideration. It is often convenient to choose your fixed location so that some of the forces create no torque around that location and therefore don't appear in the Angular Momentum Principle.