This summary presents an abridged version of the chapter, including the important equations and all available learning aids. For convenient reference, the learning aids (including the text’s examples) are placed next to or immediately after the relevant equation or discussion.
|
Interactive LearningWare examples are solved according to a five-step interactive format that is designed to help you develop problem-solving skills. |
Concept Simulations are animated versions of text figures or animations that illustrate important concepts. You can control parameters that affect the display, and we encourage you to experiment. |
|
|
Interactive Solutions offer specific models for certain types of problems in the chapter homework. The calculations are carried out interactively. |
Self-Assessment Tests include both qualitative and quantitative questions. Extensive feedback is provided for both incorrect and correct answers, to help you evaluate your understanding of the material. |
|
|
Topic |
Discussion |
Learning Aids | |||||||||||||||||||||||||||||||||||||
|
Displacement vector |
3.1 Displacement, Velocity, and Acceleration The position of an object is located with a vector r drawn from the coordinate origin to the object. The displacement 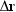 of the object is defined as of the object is defined as 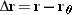 , where r and , where r and 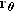 specify its final and initial positions, respectively. specify its final and initial positions, respectively. |
|
|||||||||||||||||||||||||||||||||||||
|
Average velocity |
The average velocity 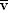 of an object moving between two positions is defined as its displacement of an object moving between two positions is defined as its displacement 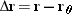 divided by the elapsed time divided by the elapsed time 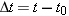 : :
|
Interactive Solution 3.11 |
|||||||||||||||||||||||||||||||||||||
|
Instantaneous velocity |
The instantaneous velocity v is the velocity at an instant of time. The average velocity becomes equal to the instantaneous velocity in the limit that the elapsed time 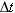 becomes infinitesimally small ( becomes infinitesimally small (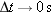 ): ):
|
|
|||||||||||||||||||||||||||||||||||||
|
Average acceleration |
The average acceleration 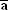 of an object is the change in its velocity of an object is the change in its velocity 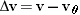 divided by the elapsed time divided by the elapsed time 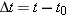 : :
|
Interactive LearningWare 3.1 |
|||||||||||||||||||||||||||||||||||||
|
Instantaneous acceleration |
The instantaneous acceleration a is the acceleration at an instant of time. The average acceleration becomes equal to the instantaneous acceleration in the limit that the elapsed time 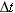 becomes infinitesimally small: becomes infinitesimally small:
|
|
|||||||||||||||||||||||||||||||||||||
|
|
3.2 Equations of Kinematics in Two Dimensions Motion in two dimensions can be described in terms of the time t and the x and y components of four vectors: the displacement, the acceleration, and the initial and final velocities. |
Example 1 |
|||||||||||||||||||||||||||||||||||||
|
Independence of the x and y parts of the motion |
The x part of the motion occurs exactly as it would if the y part did not occur at all. Similarly, the y part of the motion occurs exactly as it would if the x part of the motion did not exist. The motion can be analyzed by treating the x and y components of the four vectors separately and realizing that the time t is the same for each component. |
|
|||||||||||||||||||||||||||||||||||||
|
Equations of kinematics for constant acceleration |
When the acceleration is constant, the x components of displacement, the acceleration, and the initial and final velocities are related by the equations of kinematics, and so are the ycomponents:
The directions of these components are conveyed by assigning a plus (+) or mius (–) sign to each one. |
|
|||||||||||||||||||||||||||||||||||||
|
Acceleration in projectile motion |
3.3 Projectile Motion Projectile motion is an idealized kind of motion that occurs when a moving object (the projectile) experiences only the acceleration due to gravity, which acts vertically downward. If the trajectory of the projectile is near the earth’s surface, ay has a magnitude of 9.80 m/s2.The acceleration has no horizontal component (ax |
Examples 2, 3, 4, 5, 6, 7, 8, 12, 13 Concept Simulations 3.1, 3.2 Interactive LearningWare 3.2 Interactive Solutions 3.35, 3.39, 3.67 |
|||||||||||||||||||||||||||||||||||||
|
Symmetries in projectile motion |
There are several symmetries in projectile motion: (1) The time to reach maximum height from any point is equal to the time spent returning from the maximum height to that point. (2) The speed of a projectile depends only on its height above its launch point, and not on whether it is moving upward or downward. |
Example 9 |
|||||||||||||||||||||||||||||||||||||
|
Use Self-Assessment Test 3.1 to evaluate your understanding of Sections 3.1, 3.2 and 3.3. |
|||||||||||||||||||||||||||||||||||||||
|
Adding relative velocities |
3.4 Relative velocity The velocity of object A relative to object B is written as vAB, and the velocity of object B relative to obeject C is vBC. The velocity of A relative to C is (note the ordering of the subcripts)
|
Example 10 Concept Simulation 3.3 Interactive Solution 3.55 |
|||||||||||||||||||||||||||||||||||||
|
|
While the velocity of object A related to object B is vAB, the velocity of B relative to A is vBA |
Example 11 |
|||||||||||||||||||||||||||||||||||||
|
Use Self-Assessment Test 3.2 to evaluate your understanding of Section 3.4. |
|||||||||||||||||||||||||||||||||||||||