Chapter 1 – Stoichiometry
Introduction
Chemistry – A Molecular Science (CAMS), the first half of this two-course sequence, stressed bonding, structure, and reactivity. The material was qualitative and stressed several types of reactions and the factors that affected their relative extents of reaction. However, as the title of this text suggests, chemistry is also a quantitative science. Chemists must not only predict the products of a reaction, they must also predict the amount of product that can be expected, and the amount of waste that must be removed. They also need to know how much energy is required or how much heat is generated by a reaction. They must also understand how the reaction occurs so that they can optimize the reaction conditions. These are the types of problems addressed in this text. We begin our study of the quantitative aspects of chemistry with stoichiometry, the science that deals with the quantitative relationships between the elements in a compound (substance stoichiometry) and between the substances in a chemical reaction (reaction stoichiometry). It is the topic of this first chapter because a thorough knowledge of stoichiometry is vital to an understanding of the material presented in this course. Understanding how quantitative data and results are presented is also important, so you should review Appendix A, Reporting Quantitative Measurements and Results, for a treatment of precision, significant figures, and rounding errors. Finally, we will set up many problems using the factor label method, so please review Appendix B, The Factor Label Method, for a discussion of this procedure.1.1 Mass and Moles
Introduction
Chemists use chemical equations to design possible routes to desired molecules and to discuss chemical processes. However, the individual molecules represented in the equations are far too small to be seen, so chemists must use a very large number of molecules in their reactions in order that the reactants and products can be observed. Indeed, the number of molecules required to make a visible sample is staggering. Consider that 1 µL of water—about 1/50th of a drop—contains about 100,000,000,000,000,000 or 1017 molecules and a typical reaction in the laboratory involves thousands of times that number. Such large numbers are cumbersome, so scientists use a more convenient unit when discussing numbers of molecules. The unit is the mole, the topic of this section.Objectives
-
•Convert between numbers of moles and numbers of particles with Avogadro's number.
-
•Convert between mass and moles with molar mass.
-
•Convert between the pressure, volume, and temperature of a gas and the number of moles with the ideal gas law.
1.1-1. Avogadro's Number
Avogadro's number, which is given below, is simply the number of items in a mole, so it also defines the mole, which is simply Avogadro's number of items. A mole is used to indicate a number of items just as a dozen is used to indicate a number of eggs. Since Avodagro's number is so large, the mole is used only for the number of atoms or molecules, but it can be used for any item. For example, it is estimated that there are about 1023–1024 stars in the universe, which is 1–10 moles. Converting from moles to atoms or molecules is done in the same way as converting dozens to items.1.5 doz = (1.5 doz)(12 items/doz) = 18 items and 1.5 mol = (1.5 mol)(6.0 × 1023 atoms/mol) = 9.0 × 1023 atoms. The mole is used simply because it is much easier to discuss the number of atoms in moles than it is as individual items.
0.10 mol H2O is a much more convenient expression than 6.0 × 1022 H2O molecules.
1.1-2. Molar Mass (Mm)
Chemists need to be able to readily prepare mixtures of reactants that have the correct atom or molecule ratios for reaction, but they certainly cannot count such large numbers. Instead, they use other more easily determined properties that are related to the numbers of atoms and/or molecules. The first such method we examine is mass. Mass can be used to "count" atoms and molecules because a mole is the number of atoms present in one gram atomic weight (the atomic weight expressed in grams) of any atom or in one gram molecular weight of any molecule. Thus, the mass of a mole of any substance, which is known as its molar mass (Mm), equals its atomic or molecular weight expressed in grams. For example, the atomic weight of Mg is 24.3, so its molar mass 24.3 g/mol, and the molecular weight of CO2 is 44.0, so its molar mass is 44.0 g/mol. Thus, molar mass allows us to quickly convert a mass into a number of moles or a number of moles into a mass. Chemists use this fact to quickly "count" the number of moles of substance by simply weighing it. Mole ↔ mass conversions are most easily done with the factor label method. It uses the units of the given quantity and those of the conversion factors to assure the proper operations are performed. To use this method, arrange the factors so that the denominator of each factor cancels the numerator of the previous quantity until the units of the answer are obtained. (See The Factor Label Method.)1.1-3. Determining Molar Mass Exercise
Exercise 1.1:
Determine the molar masses of the following. Express all answers to the nearest whole number.
N2F4
Atomic weight of N
14_0__
The atomic weight of N is 14.

Atomic weight of F
19_0__
The atomic weight of F is 19.

Molar mass of N2F4
104_0__
2(14) g N/mol + 4(19) g F/mol = 104 g/mol
g/mol

Ca3(PO4)2
Atomic weight of Ca
40_0__
The atomic weight of Ca is 40.

Atomic weight of P
31_0__
The atomic weight of P is 31.

Atomic weight of O
16_0__
The atomic weight of O is 16.

Molar mass of Ca3(PO4)2
310_0__
3(40) g Ca/mol + 2(31) g P/mol + 8(16) g O/mol = 310 g/mol
g/mol

1.1-4. Mass-Mole Conversion Exercises
Exercise 1.2:
What is the mass of 3.24 mol N2O5?
Molar mass
Mm =
108_0__
2(14) g N/mol + 5(16) g O/mol = 108 g/mol
g/mol

Mass
m =
350_0__

3.24 mol N2O5 ×
= 350 g N2O5
g
| 108 g N2O5 |
| 1 mol N2O5 |
How many moles of N2O5 are in 12.7 g?
Moles
n =
0.118_0__

12.7 g N2O5 ×
= 0.118 mol N2O5
mol
| 1 mol N2O5 |
| 108 g N2O5 |
1.1-5. Moles-Items Exercise
Exercise 1.3:
How many Al atoms are present in 0.065 g Al?
Moles of atoms
n =
2.4e-3_0__

0.065 g Al ×
= 2.4e−3 mol Al
mol
| 1 mol Al |
| 27 g Al |
Individual atoms
N =
1.4e21_0__

2.4e−3 mol Al ×
= 1.4e21 atoms Al
atoms
| 6.02e23 atoms Al |
| 1 mol Al |
1.1-6. Ideal Gas Law
The number of moles of molecules in a gas can also be determined with the ideal gas law.-
•P is the pressure of the gas in atmospheres. 1 atm = 760 torr
-
•V is its volume in liters.
-
•n is the number of moles of gas.
-
•R = 0.08206 L·atm·K–1·mol–1 is the ideal gas law constant.
-
•T is the temperature on the Kelvin scale (K = °C + 273.15).
1.1-7. Gas Law Exercise
Exercise 1.4:
How many moles of H2 are in a 3.06 L container at 22 °C if its pressure is 742 torr?
P =
0.976_0__

742 torr ×
= 0.976 atm
atm
| 1 atm |
| 760 torr |
V =
3.06_0__
The volume is given in liters in the question.
L

R = 0.08206 L·atm·K–1·mol–1
T =
295_0__
The temperature must be on the Kelvin scale: T = 22 °C + 273.15 = 295 K
K

n =
0.123_0__

n =
=
= 0.123 mol
mol H2
| PV |
| RT |
| (0.976)(3.06) |
| (0.08206)(295) |
1.2 Determining Chemical Formulas
Introduction
The composition of a compound is given in terms of the mass percents of its component elements. In this section, we show how these fractions can be determined from the chemical formula of the compound and how the chemical formula can be determined from the fractions.Objectives
-
•Determine the mass composition of a compound from experimental data.
-
•Determine the mass composition from the formula of the compound.
-
•Determine the amount of one element that is combined with a known amount of another element or is present in a known amount of compound.
-
•Determine the simplest formula of a compound from the relative amounts of each of the elements present in a sample.
-
•Determine a molecular formula from its simplest formula and molar mass.
-
•Use the empirical formula and the molar mass of a substance to determine its molecular formula.
1.2-1. Experimental Mass Composition
The mass fraction of an element in a compound is the mass of the element divided by the mass of the compound in which it is found. The mass percent of an element in a compound is its mass fraction expressed as a percent. The elemental composition of a compound is frequently given by the mass percents of the elements. As shown in the following example, the elemental composition of lead(II) chloride is 74.4% Pb and 25.6% Cl by mass.1.2-2. Composition Exercise
Exercise 1.5:
A 0.2986 g sample of an oxide of iron contains 0.2161 g Fe. What is the percent iron in the sample?
|
0.2161 _0__
The numerator in the determination of a percent by mass must be the mass of the element.
g Fe
|
× 100% = |
72.37_0__
Calculate the amount using the other values.
% Fe
|
|
0.2986_0__
The denominator in the determination of a percent by mass must be the mass of the compound.
g compound
|
1.2-3. Mass Composition from Chemical Formulas
The elemental composition of a compound can be determined from its formula because its molar mass and the mass contributed by each element to its molar mass are known.Example:
One mole of PbCl2 contains:
Consequently, 278 g of PbCl2 contains 207 g Pb and 71.0 g Cl, so the elemental composition of lead chloride can be expressed as follows:
× 100% = 74.5% Pb
and
× 100% = 25.5% Cl
One mole of PbCl2 contains:
| (1 mol Pb)(207 g/mol Pb) + (2 mol Cl)(35.5 g/mol Cl) | = | 207 g Pb + 71.0 g Cl |
| = | 278 g PbCl2 |
| 207 g Pb |
| 278 g of PbCl2 |
| 71.0 g Cl |
| 278 g of PbCl2 |
-
•(a mol A)(molar mass of A) grams of A
-
•(b mol B)(molar mass of B) grams of B
1.2-4. Mass Percent Exercise
Exercise 1.6:
What is the mass percent of Na in Na2SO4? Express your answer as a percent to the nearest whole number.
The mass of one mole of Na2SO4 is:
142_0__
(2 mol Na)(23 g Na/mol Na) + (1 mol S)(32 g S/mol S) + (4 mol O)(16 g O/mol O) = 142 g
g

The mass of Na in one mole of Na2SO4 is:
46_0__
(2 mol Na)(23 g Na/mol Na) = 46 g
g

The fraction of the mass of Na2SO4 that is due to sodium expressed as a percent is:
32_0__
× 100% = 32%
%

| 46 g Na |
| 142 g Na2SO4 |
1.2-5. Mass Percent Exercise
Exercise 1.7:
Determine the mass percent of P in Ca3(PO4)2. Express your answer as a percent to the nearest whole number.
The mass of one mole of Ca3(PO4)2 is:
310_0__
(3 mol Ca)(40 g/mol) + (2 mol P)(31 g/mol) + (8 mol O)(16 g/mol) = 310 g
g

The mass of P in one mole of Ca3(PO4)2 is:
62_0__
(2 mol P)(31 g/mol) = 62 g
g

The fraction of the mass of Ca3(PO4)2 that is due to phosphorus expressed as a percent is:
20_0_2_
× 100% = 20.%
%

| 62 g P |
| 310 g Ca3(PO4)2 |
1.2-6. Using Mass Percents
While an elemental mass fraction has no units, units are implied in factor label problems because the fraction is determined to be (mass of element)/(mass of compound). Consequently, mass fractions can be used to convert between the mass of an element and the mass of the compound. Similarly, the mass percent of an element in a compound can be viewed as the mass of the element present in 100 g of compound. Thus, the fact that XY is 30% X by mass implies that there are 30 g X/100 g XY. Furthermore, the sum of the elemental percents of all the elements in a compound must sum to 100%, so we can deduce the percent of one element in a compound if we know the percents of all other elements in the compound. Thus, if XY is 30% X by mass, then it must also be 70% Y by mass.Example:
Lead chloride is 74.4% lead by mass. How much lead is present in 23.4 g of lead chloride? The percent is expressed as 74.4 g Pb/100 g compound, which is the factor required for the conversion.
What is the percent chloride in lead chloride?
The compound contains only Pb and Cl, so the sum of the percents of the two elements must be 100%. However, PbCl2 is 74.4% Pb, so
Thus, PbCl2 is 74.4% Pb and 25.6% Cl by mass.
Lead chloride is 74.4% lead by mass. How much lead is present in 23.4 g of lead chloride? The percent is expressed as 74.4 g Pb/100 g compound, which is the factor required for the conversion.
23.4 g compound ×
= 17.4 g Pb
| 74.4 g Pb |
| 100 g compound |
%Cl = 100% – %Pb = 100.0 – 74.4 = 25.6% Cl
1.2-7. Composition Exercise
Exercise 1.8:
Hexane (C6H14) is 83.7% carbon by mass.
What portion, expressed as a percent, of the mass of hexane is due to hydrogen?
%H =
16.3_0__
%H = 100% – %C
%

How many grams of hexane contain 13.6 g C?
|
13.6_0__
Start with the amount you wish to convert.
g C
|
= |
100_0__
This entry is part of the percent C.
g C6H14
|
= |
16.2_0__
Calculate the amount using the other values.
g C6H14
|
|
83.7_0__
The factor is the percent C, which is expressed as a ratio of masses.
g C
|
1.2-8. Empirical Formula
The elemental composition can be used to determine the ratio of elemental masses in a compound. Molar masses can then be used to convert the ratio of elemental masses into one of moles, and the ratio of moles is the ratio of subscripts in the compound. We cannot determine the actual subscripts without more information, but we can determine the simplest set of integers that results in the correct ratios. The formula of a compound that uses this simplest set of integers is called the empirical formula or the simplest formula. To determine the empirical or simplest formula of a compound from its elemental composition:-
1Convert the amount of each element in a sample into moles of the element.
-
2Determine the ratio of the moles by dividing each by the smallest.
-
3If the result of Step 2 is not an integer, convert the ratio to a ratio of simple whole numbers. This is most easily accomplished by identifying the fraction that corresponds to the decimal, and then multiplying the ratio by the integer that makes the ratio an integer. See Table 1.1: Some Common Decimals and their Multipliers.
| Step 2 | Multiplier | Step 2 | Multiplier | |
|---|---|---|---|---|
| 0.125 | 8 | 0.5 | 2 | |
| 0.167 | 6 | 0.625 | 8 | |
| 0.200 | 5 | 0.667 | 3 | |
| 0.250 | 4 | 0.75 | 4 | |
| 0.333 | 3 | 0.833 | 6 | |
| 0.375 | 8 | 0.875 | 8 |
Table 1.1: Some Common Decimals and their Multipliers
For example, to convert a H:C mole ratio in Step 2 of 2.667 to a ratio of small whole numbers, you can recognize that the number means 2.667 mol H/1 mol C and that 0.667, which is a ratio of 2/3 or use the above table to determine that the multiplier must be 3. Multiply the numerator and denominator of the ratio by 3 to eliminate the fraction. The result is 3(2.667)/3(1) = 8 mol H/3 mol C. The formula of the compound is C3H8.
1.2-9. Empirical Formula Exercise
Exercise 1.9:
6.84 g of an oxide of chromium is found to contain 4.68 g Cr. What is the empirical formula of the oxide? Assume that the compound contains only Cr and O. Express all answers to three significant digits.
The number of moles of each element in the sample is:
moles of Cr (Mm = 52.0 g/mol) in the sample:
0.0900_0_3_

4.68 g Cr ×
= 0.0900 mol Cr
mol Cr
| 1 mol Cr |
| 52.0 g Cr |
moles of O in the sample:
0.135_0__
mass of oxygen = mass of sample – mass of Cr = 6.84 – 4.68 = 2.16 g O
mol O

2.16 g O ×
= 0.135 mol
| 1 mol O |
| 16.0 g O |
The ratio of the larger number of moles to the smaller number of moles (mol O/mol Cr) is:
1.5_0_3_
=

| 0.135 mol O |
| 0.0900 mol Cr |
| 1.50 mol O |
| 1.00 mol Cr |
The ratio determined in the previous step as a ratio of whole numbers (For example, 1.33 mol O/mol Cr would be expressed as 4/3) is:
o_3/2_ins
×
=

| 1.50 mol O |
| 1.00 mol Cr |
| 2 |
| 2 |
| 3 mol O |
| 2 mol Cr |
The empirical formula is the following. (Denote any subscripts with an underscore. For example, NH_3 for NH3.)
o_Cr_2O_3_s
There are 2 mol Cr for every 3 mol of O, so the empirical formula of this oxide of chromium is Cr2O3.

1.2-10. Empirical Formula Exercise
Exercise 1.10:
When hydrocarbons (compounds that contain only C and H) are burned, all of the carbon is converted into CO2 and all of the hydrogen into H2O. What is the empirical formula of a hydrocarbon that produces
0.200 mol CO2 and 0.125 mol H2O when burned?
0.200 mol CO2 and 0.125 mol H2O when burned?
The number of moles of carbon in the sample is:
0.200_0_3_
All of the carbon in the hydrocarbon is converted into CO2, so we convert the number of moles of CO2 into moles of carbon. There is one mole of carbon in 1 mole of CO2, so the following conversion produces the answer.

0.200 mol CO2 ×
= 0.200 mol C
| 1 mol C |
| 1 mol CO2 |
The number of moles of hydrogen in the sample is:
0.250_0_3_
All of the hydrogen in the hydrocarbon is converted into H2O, so we simply convert the number of moles of H2O into moles of hydrogen. There are two moles of hydrogen in 1 mole of H2O, so the following conversion produces the answer.

0.125 mol H2O ×
= 0.250 mol H
| 2 mol H |
| 1 mol H2O |
The ratio of the larger to the smaller number of moles is:
1.25_0__
= 1.25 mol H/mol C

| 0.250 mol H |
| 0.200 mol C |
The above number expressed as a ratio of whole numbers is:
o_5/4_ins
Multiply the numerator and denominator by 4 to eliminate the 0.25 in the ratio and obtain 5/4, a ratio of small whole numbers.

The empirical formula of the hydrocarbon is the following. (Denote any subscripts with an underscore. For example, NH_3 for NH3.)
o_C_4H_5_s
There are 4 mol C for every 5 mol of H, so the empirical formula of this hydrocarbon is C4H5.

1.2-11. Empirical Formulas from Elemental Compositions
To determine the empirical formula of a compound from its percent composition, use the percents as if they were masses in grams and proceed as in the previous topic.
-
1Divide the mass percent of each element by its molar mass to determine the number of moles of the element present in 100 g of sample.
-
2Divide each of the moles determined in Step 1 by the smallest number of moles to get simple ratios.
-
3If any of the results of Step 2 are not integers, multiply all of the numbers by the integer that makes them integers.
-
4The integers determined in Step 3 are the subscripts in the empirical formula.
1.2-12. Empirical Formula from Elemental Composition Exercise
Exercise 1.11:
A hydrocarbon (a compound that contains only carbon and hydrogen) is found to be 82.66% C and
17.34% H by mass. What is the empirical formula of the hydrocarbon? Use molar masses of 12.01 g/mol and 1.008 g/mol for C and H, respectively.
17.34% H by mass. What is the empirical formula of the hydrocarbon? Use molar masses of 12.01 g/mol and 1.008 g/mol for C and H, respectively.
The number of moles of C in 100 g of compound is:
6.883_0__

82.66 g C ×
= 6.883 mol C
| 1 mol C |
| 12.01 g C |
The number of moles of H in 100 g of compound is:
17.20_0_4_

17.34 g H ×
= 17.20 mol H
| 1 mol H |
| 1.008 g H |
The ratio expressed as a decimal of the smaller number to the larger number of moles is:
2.499_0__
=

| 17.20 mol H |
| 6.883 mol C |
| 2.499 mol H |
| 1 mol C |
The ratio in Step 3 expressed as a ratio of whole numbers is:
o_5/2_ins
Multiply the numerator and denominator of Step 2 by 2 to eliminate the fraction.
×
=

| 2 |
| 2 |
| 2.499 mol H |
| 1 mol C |
| 5 mol H |
| 2 mol C |
The empirical formula is the following. (Denote any subscripts with an underscore. For example, NH_3 for NH3.)
o_C_2H_5_s
There are 2 mol C for every 5 mol of H, so the empirical formula of this hydrocarbon is C2H5.

1.2-13. Molecular Formulas
A molecular formula of a compound, which shows the actual number of atoms present in a molecule, can be determined from its empirical formula and molar mass.
| molecular formula | n | molar mass (g/mol) |
|---|---|---|
| C12H12 | 12 | 13 × 12 = 156 |
| C6H6 | 6 | 13 × 6 = 78 |
| C4H4 | 4 | 13 × 4 = 52 |
Table 1.2
We use the fact that molar mass of the compound = n × molar mass of the empirical unit to determine the value of n as follows:
Once we have the value of n, we can write the molecular formula by simply multiplying each of the subscripts in the empirical formula by n. For example, to determine the molecular formula of a compound with an empirical formula of CH2 (Mm = 14 g/mol) and a molar mass of 112 g/mol, we would first determine n as
n =
= 8
| 112 g/mol |
| 14 g/mol |
1.2-14. Molecular Formula Exercise
Exercise 1.12:
Write the empirical formula for each of the following molecular formulas. (Denote any subscripts with an underscore. For example, NH_3 for NH3.)
C4H10N4:
o_C_2H_5N_2_s
Each of the subscripts is divisible by 2.

C12H24N5:
o_C_12H_24N_5_s
There is no common factor of the subscripts, so this molecular formula is also the empirical formula.

C8H8N4:
o_C_2H_2N_s
Each of the subscripts is divisible by 4.

1.2-15. Molecular Formula from Empirical Formula Exercise
Exercise 1.13:
What is the molecular formula of a compound that has an empirical formula of C2H4O and a molar mass of 88 g/mol?
| n = |
88_0__
This entry is the molar mass of the compound.
g/mol
|
= |
2_0__
This is the result of the division: (88 g/mol) / (44 g/mol) = 2.
|
|
44.051___
This entry is the molar mass of the empirical unit.
g/mol
|
The empirical formula of the compound is the following. (Denote any subscripts with an underscore. For example, NH_3 for NH3.)
o_C_4H_8O_2_s
Multiply the subscripts of the empirical formula by the value of n determined above to get the molecular formula.

1.2-16. Molecular Formula Exercise
Exercise 1.14:
What is the molecular formula of a compound that is 64.27% C, 7.19% H, and 28.53% O and has a molar mass of about 220 g/mol?
100.00 g of this compound contains how many moles of each element?
C
5.351_0_4_
The mass of each element present in 100 g of a compound equals its mass percent in grams.
mol

64.27 g C ×
= 5.351 mol C
| 1 mol C |
| 12.011 g C |
H
7.13_0_3_
The mass of each element present in 100 g of a compound equals its mass percent in grams.
mol

7.19 g H ×
= 7.13 mol H
| 1 mol H |
| 1.008 g C |
O
1.783_0__
The mass of each element present in 100 g of a compound equals its mass percent in grams.
mol

28.53 g O ×
= 1.783 mol O
| 1 mol O |
| 15.999 g O |
The number of moles of each element divided by the smallest number of moles is:
C
3___
Oxygen is present in the smallest number of moles, so this entry is the number of moles of C present divided by the number of moles of O present.
=
mol

| 5.351 mol C |
| 1.783 mol O |
| 3 mol C |
| 1 mol O |
H
4___
Oxygen is present in the smallest number of moles, so this entry is the number of moles of H present divided by the number of moles of O present.
=
mol

| 7.13 mol H |
| 1.783 mol O |
| 4 mol H |
| 1 mol O |
O
1___
Oxygen is present in the smallest number of moles, so this entry is the number of moles of O present divided by the number of moles of O present.
mol

The empirical formula of the compound is the following. (Denote any subscripts with an underscore. For example, NH_3 for NH3.)
o_C_3H_4O_s
There are 3 mol C and 4 mol H for each 1 mol O, so the empirical formula = C3H4O.

The number of empirical units present in one molecular unit is:
4___
The molar mass of the simplest unit (C3H4O) is 56 g/mol (3(12) + 4(1) + 1(16)), while the molar mass of the compound is ~220 g/mol, so

n =
= ~4
| ~220 g/mol |
| 56 g/mol |
The molecular formula is the following. (Denote any subscripts with an underscore. For example, NH_3 for NH3.)
o_C_12H_16O_4_ins
The molecular formula consists of n empirical formulas, where n was determined in the previous step to be 4. The molecular formula is C12H16O4.

1.2-17. Molecular Formula from Combustion Exercise
Exercise 1.15:
It is common to determine formulas of organic compounds by burning them and determining the mass fractions of carbon and hydrogen from the amounts of CO2 and H2O that are produced in the combustion. If the compound contains oxygen, the mass of oxygen must be determined from the total mass of the sample and the masses of C and H that it contains.
What is the empirical formula of ascorbic acid (vitamin C) if combustion of 0.579 g of ascorbic acid produces 0.868 g of CO2 and 0.237 g H2O? Ascorbic acid also contains oxygen.
Convert mass of CO2 and H2O to moles.
moles of CO2 produced:
0.0197_0__

0.868 g CO2 ×
= 0.0197 mol CO2
mol CO2
| 1 mol CO2 |
| 44.01 g CO2 |
moles of C present in the CO2:
0.0197_0__

0.0197 mol CO2 ×
= 0.0197 mol C
mol C
| 1 mol C |
| 1 mol CO2 |
moles of H2O produced:
0.0132_0__

0.237 g H2O ×
= 0.0132 mol H2O
mol H2O
| 1 mol H2O |
| 18.02 g H2O |
moles of H present in the H2O:
0.0264_0__

0.0132 mol H2O ×
= 0.0264 mol H
mol H
| 2 mol H |
| 1 mol H2O |
The sample contains oxygen, so its mass must be determined by difference. Therefore, the mass of C and H must be determined
from the number of moles above. Note: this step would not be necessary if the sample contained no oxygen. We would simply determine
the mol H/mol C ratio with the numbers of moles determined above to get the empirical formula.
mass of C in sample:
0.237_0__

0.0197 mol C ×
= 0.237 g C
g C
| 12.01 g C |
| 1 mol C |
mass of H in sample:
0.0265_0__

0.0263 mol H ×
= 0.0265 g H
g H
| 1.008 g H |
| 1 mol H |
mass of oxygen in sample:
0.316_0__
mass O = mass of sample – mass C – mass H = 0.579 g Ascorbic – 0.237 g C – 0.0265 g H = 0.316 g O
g O

moles of oxygen in sample:
0.0197_0__

0.316 g O ×
= 0.0197 mol O
mol O
| 1 mol O |
| 16.00 g O |
Determine the mole ratios.
mol C/mol C =
1_0__
The ratio of a substance to itself is always 1.

mol H/mol C =
1.33_0_3_
= 1.33 mol H/mol C

| 0.0263 mol H |
| 0.0197 mol O |
mol O/mol C =
1_0_3_
= 1.00 mol O/mol C

| 0.0197 mol O |
| 0.0197 mol O |
Multiplier to be used to convert all of the above to integers:
3_0__
The .33 decimal calls for a multiplier of 3.

The subscripts in the empirical formula:
subscript of C =
3_0__
3(1 mol C/mol C) = 3

subscript of H =
4_0__
3(1.33 mol H/mol C) = 4

subscript of O =
3_0__
3(1 mol O/mol C) = 3

The molar mass of ascorbic acid is 176 g/mol. What is its molecular formula?
The molar mass of the empirical unit =
88.059___
3(12.01) + 4(1.008) + 3(16.00) = 88.1 g/mol
g/mol

The number of empirical units in a molecular unit =
2_0__
= 2 empirical unit/molecular unit
units

| 176 g/molecular unit |
| 88.1 g/empirical unit |
The subscripts in the molecular formula:
subscript of C =
6_0__
2(3) = 6

subscript of H =
8_0__
2(4) = 8

subscript of O =
6_0__
2(3) = 6

1.3 Substance or Composition Stoichiometry
Introduction
In a composition stoichiometry problem, the amount of one substance that is combined with another is determined with the use of the ratios of the subscripts in the chemical formula.Objectives
-
•Determine and use stoichiometric links derived from chemical formulas.
1.3-1. Stoichiometric Link Video
Stoichiometric Link
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•View the video full screen in another window.
-
•View the video in text format by scrolling down.
1.3-2. Stoichiometric Links and Chemical Formulas
The stoichiometric links for a substance are formed from the subscripts in a chemical formula.
|
|
|
Table 1.3
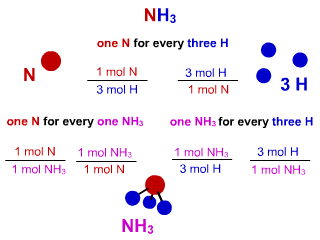
Figure 1.1: Substance Stoichiometry in NH3
|
Conversion factors using H in H2SO4 |
Conversion factors using S in H2SO4 |
Conversion factors using O in H2SO4 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Table 1.4
1.3-3. Using the Stoichiometric Link
Stoichiometric links can be combined with the factor label method to determine the amount of any element in a compound that is combined with a known amount of any other element in the compound.
1.3-4. Mass-Mass Conversion
We have seen that the heart of a substance stoichiometry problem is multiplying the given number of moles by the appropriate stoichiometric link to obtain the number of moles of the desired substance. We now combine that operation with the molar masses of the given and desired substances to determine the mass of one substance (the desired substance) that is combined with a given mass of another (the given substance). The process involves the following three conversions:-
1mass A → mol A: Convert the given mass into given moles with the molar mass of the given substance.
-
2mol A → mol B: Multiply the given moles calculated in Step 1 by the appropriate stoichiometric link to obtain the desired moles.
-
3mol B → mass B: Convert the desired moles determined in Step 2 into grams with the molar mass of the desired substance.
12.2 g Al ×
×
×
= 10.8 g O
| 1 mol Al |
| 27.0 g Al |
| 3 mol O |
| 2 mol Al |
| 16.0 g O |
| 1 mol O |
1.3-5. Mole Atom-Mole Molecule Conversion Exercise
Exercise 1.16:
How many moles of MgCl2 contain 0.64 mol Cl atoms?
|
0.64_0__
Start with the given amount.
mol Cl
|
× |
1_0__
This is the numerator of the stoichiometric link, so it must have the units of 'mol desired.' It is equal to the subscript of the desired substance in the chemical formula.
mol MgCl2
|
= |
0.32_0__
Calculate the amount using the other values.
mol MgCl2
|
|
2_0__
The preceding amount is 'mol given,' so this entry is the denominator of the stoichiometric link. It must have the units of 'mol given' and is equal to the subscript of the given substance in the chemical formula.
mol Cl
|
1.3-6. Mole Atom-Mole Atom Conversion Exercise
Exercise 1.17:
How many moles of hydrogen atoms are in a sample of C6H14 that contains 0.25 mol C?
|
0.25_0__
Start with the amount you wish to convert.
mol C
|
× |
14_0__
This is the numerator of the stoichiometric link, so it must have the units of 'mol desired.' It is equal to the subscript of the desired substance in the chemical formula.
mol H
|
= |
0.58_0__
Calculate the amount using the other values.
mol H
|
|
6_0__
The preceding amount is 'mol given,' so this entry is the denominator of the stoichiometric link. It must have the units of 'mol given' and is equal to the subscript of the given substance in the chemical formula.
mol C
|
1.3-7. Mass Atom-Mass Molecule Conversion Exercise
Exercise 1.18:
What mass of Fe3O4 (Mm = 232 g/mol) contains 12 g of iron (Mm = 55.9 g/mol)?
|
12_0__
Start with the amount you wish to convert.
g Fe
|
× |
1 _0__
This entry must have the units 'mol given' and is part of the molar mass.
mol Fe
|
× |
1_0__
This is the numerator of the stoichiometric link, so it must have the units of 'mol desired.' It is equal to the subscript of the desired substance in the chemical formula.
mol Fe3O4
|
× |
232_0__
This entry is part of the molar mass of the sought substance, but it must have the units of the answer.
g Fe3O4
|
= |
17_0__
Calculate the amount using the other values.
g Fe3O4
|
|
55.9_0__
This entry must have the units 'mol given' and is part of the molar mass.
g Fe
|
3_0__
The preceding amount is 'mol given,' so this entry is the denominator of the stoichiometric link. It must have the units of 'mol given' and is equal to the subscript of the given substance in the chemical formula.
mol Fe
|
1_0__
Convert 'mol sought' to 'g sought' with the molar mass. This denominator must have the same units as the preceding numerator.
mol Fe3O4
|
1.3-8. Mass Atom-Mass Atom Conversion Exercise
Exercise 1.19:
What mass of Fe (Mm = 55.9 g/mol) is combined with 26.3 g chlorine (Mm = 35.5 g/mol) in FeCl3?
|
26.3_0__
Start with the amount you wish to convert.
g C
|
× |
1_0__
This entry must have the units 'mol given' and is part of the molar mass.
mol Cl
|
× |
1_0__
This is the numerator of the stoichiometric link, so it must have the units of 'mol desired.' It is equal to the subscript of the desired substance in the chemical formula.
mol Fe
|
× |
55.9 _0__
This entry is part of the molar mass of the sought substance, but it must have the units of the answer.
g Fe
|
= |
13.8_0__
Calculate the amount using the other values.
g Fe
|
|
35.5_0__
Convert 'g given' to 'mol given' with the molar mass. Remember, the denominator of the factor must have the same units as the preceding numerator.
g Cl
|
3_0__
The preceding amount is 'mol given,' so this entry is the denominator of the stoichiometric link. It must have the units of 'mol given' and is equal to the subscript of the given substance in the chemical formula.
mol Cl
|
1_0__
Convert 'mol sought' to 'g sought' with the molar mass. This denominator must have the same units as the preceding numerator.
mol Fe
|
1.4 Balancing Chemical Equations
Introduction
Neither the identity nor the number of atoms is changed in a chemical reaction, so chemical equations are balanced to assure that the number of each type of atom is the same on both sides. This is done by changing the number of each reacting and produced molecule by placing coefficients in front of each species. In this section, we show how to balance simple chemical equations by inspection.Objectives
-
•Balance a chemical equation by inspection.
1.4-1. Balancing Chemical Equations Video
Balancing Chemical Equations
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•View the video full screen in another window.
-
•View the video in text format by scrolling down.
1.4-2. Procedure for Balancing Equations
Chemical equations are balanced to assure that the number of each type of atom is the same on both sides of the equation. Only coefficients (not subscripts) can be changed to balance a chemical equation.
-
1Pick the molecule with the greatest number of atoms and set its coefficient to "1" unless another choice is obviously better. For example, sometimes a "2" must be used to assure an even number of one of the atoms.
-
2Determine which atoms are fixed by the coefficient set in Step 1, then balance those atoms on the other side of the equation.
-
3Determine which atoms are fixed by the coefficient(s) created in Step 2, then balance those atoms on the other side of the equation.
-
4Repeat Step 3 until the equation is balanced.
Example:
As an example, we will follow the steps above to balance the following chemical equation:
As an example, we will follow the steps above to balance the following chemical equation:
____ HCl + ____ MnO2 → ____ MnCl2 + ____ H2O + ____ Cl2
1
Make the coefficient of either MnO2 or MnCl2 one. We choose MnO2.
____ HCl + 1 MnO2 → ____ MnCl2 + ____ H2O + ____ Cl2
2
The coefficient used in Step 1 fixes the number of Mn atoms at 1 and O atoms at 2, so we balance the Mn atoms with a coefficient of 1 for MnCl2 and the oxygen atoms with a coefficient of 2 for water.
____ HCl + 1 MnO2 → 1 MnCl2 + 2 H2O + ____ Cl2
3
The coefficient of water fixes the number of hydrogen atoms at four, so we balance the H atoms with a coefficient of 4 for HCl. Note that the coefficient of MnCl2 does not fix the number of Cl atoms because it is not the only source of Cl.
4 HCl + 1 MnO2 → 1 MnCl2 + 2 H2O + ____ Cl2
4
The coefficient of HCl fixes the number of chlorine atoms at four, but there are already 2 Cl atoms in 1 MnCl2, so we balance the Cl atoms on the other side of the equation with a coefficient of 1 for Cl2.
4 HCl + 1 MnO2 → 1 MnCl2 + 2 H2O + 1 Cl2
5
Each side of the equation contains 4 H atoms, 1 Mn atom, 2 O atoms, and 4 Cl atoms. The equation is now balanced, but ones are not usually written. Thus, the balanced equation is usually written as shown in the last step.
4 HCl + MnO2 → MnCl2 + 2 H2O + Cl2
1.4-3. Balancing Equations Exercise
Exercise 1.20:
Balance the following equations with the smallest whole-number coefficients. Include coefficients of "1" in your answer.
2_0__
Start with 2 N2O5 to assure an even number of O atoms.
N2

+
5_0__
Start with 2 N2O5 to assure an even number of O atoms.
O2

→
2_0__
Start with 2 N2O5 to assure an even number of O atoms.
N2O5

2_0__
Start with 2 NaOH to avoid fractions.
Na

+
2_0__
Start with 2 NaOH to avoid fractions.
H2O

→
2_0__
Start with 2 NaOH to avoid fractions.
NaOH

+
1_0__
Start with 2 NaOH to avoid fractions.
H2

1_0__
Start with 1 P4.
P4

+
6_0__
Start with 1 P4.
Cl2

→
4_0__
Start with 1 P4.
PCl3

1_0__
Start with 1 C6H12O6.
C6H12O6

+
6_0__
Start with 1 C6H12O6.
O2

→
6_0__
Start with 1 C6H12O6.
CO2

+
6_0__
Start with 1 C6H12O6.
H2O

1.5 Reaction Stoichiometry
Introduction
The ratios of the coefficients of a balanced equation are conversion factors that allow us to calculate the amount of one substance that is produced by or reacts with a given amount of another substance. The only difference between this process and the one used to determine how much of one element was combined with a given amount of another element in a compound is the stoichiometric ratio or link: in one, the stoichiometric link is the ratio of the subscripts in the chemical formula; in the other, it is the ratio of the coefficients in the balanced equation. All other operations are the same in the two problem types.Objectives
-
•Write the stoichiometric ratio relating two substances involved in a chemical reaction.
-
•Use the ratio to convert the amount of one substance involved in the reaction to the chemically equivalent amount of another substance in the same reaction.
-
•Identify the limiting reactant in a reaction.
-
•Determine the amount of product formed or of reactant consumed from the amount of limiting reactant that reacts.
-
•Determine the percent yield given the actual yield of a reaction or use the percent yield to determine the actual yield.
-
•Determine the complete composition of a reaction mixture after the reaction is complete.
1.5-1. Stoichiometric Links in Chemical Reactions
Stoichiometric links formed from the coefficients of balanced chemical equations are used to convert between equivalent amounts of reactants and products in a reaction.
N2 + 3 H2 → 2 NH3
|
|
|
Table 1.5
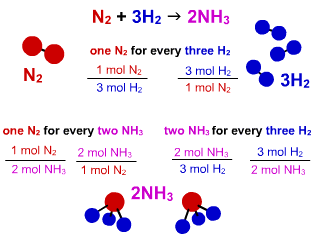
Figure 1.2: Reaction Stoichiometry in the Formation of NH3 Reaction
1.5-2. Using Stoichiometric Links for Chemical Reactions
The stoichiometric links produced by the coefficients in a balanced equation can be used to determine the number of moles of one substance that are produced by or react with a given number of moles of another substance in the equation.Example:
The following shows how to determine the number of moles of nitrogen that are required and how many moles of NH3 are produced in the reaction of 3.6 moles of hydrogen in the following:
The following shows how to determine the number of moles of nitrogen that are required and how many moles of NH3 are produced in the reaction of 3.6 moles of hydrogen in the following:
3 H2 + N2 → 2 NH3
3.6 mol H2 ×
| = | 1.2 mol N2 are required | ||
3.6 mol H2 ×
| = | 2.4 mol NH3 are produced |
1.5-3. Mole-Mole Conversion Exercise
Exercise 1.21:
How many moles of hydrogen are required to produce 2.8 mol NH3? The chemical equation is
N2 + 3 H2 → 2 NH3
|
2.8_0__
Start with the amount you wish to convert.
mol NH3
|
× |
3_0__
This is the numerator of the stoichiometric link, so it must have the units of 'mol desired.' It is equal to the coefficient of the desired substance in the chemical equation.
mol H2
|
= |
4.2_0__
Calculate the amount using the other values.
mol H2
|
|
2_0__
The preceding amount is 'mol given,' so this entry is the denominator of the stoichiometric link. It must have the units of 'mol given' and is equal to the coefficient of the given substance in the chemical equation.
NH3
|
1.5-4. Method for Mass-Mass Conversions
We finish this lesson by showing how to determine the mass of one substance that reacts with or is produced by the reaction of a given mass of another substance in the chemical equation. The process, which is identical to that used in determining the mass of one element that is combined with a given mass of another element in a compound, involves the following three conversions:-
1mass A → mol A: Use the molar mass of the given compound to convert its mass to moles.
-
2mol A → mol B: Use the stoichiometric link (ratio of coefficients) to convert the number of moles of given compound determined in Step 1 into the equivalent number of moles of desired substance.
-
3mol B → mass B: Use the molar mass of the desired substance to convert the number of moles determined in Step 2 into the mass of the desired substance.
1.5-5. Mass-Mass Conversion Exercise
Exercise 1.22:
How many grams of fluorine must react to produce 24 g PF5 (Mm = 126 g/mol)?
|
24_0__
Start with the amount you wish to convert.
g PF5
|
× |
1_0__
This entry must have the units 'mol given' and is part of the molar mass.
mol PF5
|
× |
10_0__
This is the numerator of the stoichiometric link, so it must have the units of 'mol desired.' It is equal to the coefficient of the desired substance in the chemical equation.
mol F2
|
× |
38_0__
This entry is part of the molar mass of the sought substance, but it must have the units of the answer.
g F2
|
= |
18_0__
Calculate the amount using the other values.
g F2
|
|
126 _0__
Convert 'g given' to 'mol given' with the molar mass. Remember, the denominator of the factor must have the same units as the preceding numerator.
g PF5
|
4 _0__
The preceding amount is 'mol given,' so this entry is the denominator of the stoichiometric link. It must have the units of 'mol given' and is equal to the coefficient of the given substance in the chemical equation.
mol PF5
|
1_0__
Convert 'mol sought' to 'g sought' with the molar mass. This denominator must have the same units as the preceding numerator.
mol F2
|
1.5-6. Limiting Reactants
Thus far, we have determined the amount of substance that reacts with or is formed by the reaction of another substance. However, there is usually more than one reactant and the reactants are not usually added in stoichiometric ratios. In such cases, one of the reactants, known as the limiting reactant, is consumed before any other reactant. The other reactants are said to be in excess because they are still available after the limiting reactant is consumed. The limiting reactant is identified as the reactant that is capable of producing the least amount of product. Thus, one way to determine which of several reactants is the limiting reactant is to determine the amount of product each reactant is capable of producing. The limiting reactant is the one that is capable of producing the least. Note, that the limiting reactant is not necessarily the reactant present in the smallest mass nor in the smallest number of moles. To determine the limiting reactant, you would determine the number of moles of a substance B that is produced or reacts with a given number of moles of reactant A. The moles of B is formed from reactant A: However, this can be rewritten as follows: The coefficient of B is constant, so the smallest amount of B would be produced by the reactant with the smallest mol/coefficient ratio. We conclude that the limiting reactant is that reactant with the smallest (mol A/coefficient A) ratio. The amount of any product that forms or reactant that reacts is equal to the (reactant moles)/(reactant coefficient) ratio of the limiting reactant times the coefficient of the product or reactant whose amount is to be determined.1.5-7. Mole-Mole Limiting Reactant Exercise
Exercise 1.23:

How many moles of NF3 can be produced from the reaction of 0.50 mol N2 and 0.90 mol F2 in the following reaction?
N2 + 3 F2 → 2 NF3
Determine mole/coefficient ratios.
N2
0.50_0_2_
= 0.50

| 0.50 mol N2 |
| 1 mol N2 |
F2
0.30_0_2_
= 0.30

| 0.90 mol F2 |
| 3 mol F2 |
The limiting reactant is
-
N2 0.30 < 0.50, so F2 is the limiting reactant.
-
F2

Moles of NF3 that can be produced by the limiting reactant is
0.60_0_2_
Multiply the mole/coefficient ratio for the limiting reactant times the coefficient of the product. 
(0.30)(2 mol NF3) = 0.60 mol NF3
mol NF3
1.5-8. Mass-Mass Limiting Reactant Exercise
Exercise 1.24:

How many grams of Ag3PO4 (Mm = 418.6 g/mol) form in the reaction of 3.21 g AgNO3
(Mm = 169.9 g/mol) and 1.65 g K3PO4 (Mm = 212.3 g/mol)? How much of the excess reactant remains?
(Mm = 169.9 g/mol) and 1.65 g K3PO4 (Mm = 212.3 g/mol)? How much of the excess reactant remains?
3 AgNO3 + K3PO4 → Ag3PO4 + 3 KNO3
Determine the number of moles of each reactant.
AgNO3
0.0189_0__

3.21 g AgNO3 ×
= 0.0189 mol
mol
| 1 mol AgNO3 |
| 169.9 g AgNO3 |
K3PO4
0.00777_0__

1.65 g K3PO4 ×
= 0.00777 mol
mol
| 1 mol K3PO4 |
| 212.3 g K3PO4 |
Determine the mol/coefficient ratios.
AgNO3
0.00630_0_3_
= 0.00630

| 0.0189 mol AgNO3 |
| 3 mol AgNO3 |
K3PO4
0.00777_0__
= 0.00777

| 0.00777 mol K3PO4 |
| 1 mol K3PO4 |
Identify the limiting reactant.
-
AgNO3
-
K3PO4 0.00630 < 0.00777, so AgNO3 is the limiting reactant.

Determine the amount of product formed.
2.64_0__
Use the mol/coefficient ratio for the limiting reactant and the coefficient of the product to obtain moles of product then use the molar mass to convert to mass.
g Ag3PO4

0.00630 × 1 mol Ag3PO4 ×
= 2.64 g Ag3PO4
| 418.6 g Ag3PO4 |
| 1 mol Ag3PO4 |
Determine the amount of excess reactant that is unreacted.
Mass of excess reactant that reacts:
1.34_0__
Use the mol/coefficient ratio for the limiting reactant and the coefficient of the other reactant to obtain moles of the other reactant that react, then use the molar mass to convert to the mass that reacts.

0.0630 × 1 mol K3PO4 ×
= 1.34 g K3PO4 reacts
g
| 212.3 g K3PO4 |
| 1 mol K3PO4 |
Mass of excess reactant that remains:
0.31_0__
There were 1.65 g initially, but 1.34 g react, so 1.65 – 1.34 = 0.31 g does not react.
g

1.5-9. Percent Yield
The mass of a product determined from the amount of limiting reactant and the stoichiometry of the reaction is known as the theoretical yield. However, the theoretical yield is not usually isolated in an actual experiment. The actual yield, which is the amount that is actually isolated in the experiment, can be less than the theoretical yield for the following reasons:-
•The reaction may not be extensive, so all of the limiting reactant does not react.
-
•Product can be lost during purification. For example, some solid may remain on the filter paper or dissolve when washed.
-
•Competing reactions can consume some of the reactants.
1.5-10. Percent Yield Exercise
Exercise 1.25:
Aspirin (C9H8O4, Mm = 180.16 g/mol) is prepared from the reaction of salicylic acid (C7H6O3,
Mm = 138.12 g/mol) and acetic anhydride (C4H6O3, Mm = 102.09 g/mol) by the following reaction:
Mm = 138.12 g/mol) and acetic anhydride (C4H6O3, Mm = 102.09 g/mol) by the following reaction:
C7H6O3 + C4H6O3 → C9H8O4 + C2H4O2
What is the percent yield of aspirin if the reaction of 20.00 g of salicylic acid and 17.00 g of acetic anhydride produces 22.36 g of aspirin?
theoretical yield of aspirin if salicylic acid is the limiting reactant:
26.09_0__

20.00 g C7H6O3 ×
×
×
= 26.09 g C9H8O4
g C9H8O4
| 1 mol C7H6O3 |
| 138.12 g C7H6O3 |
| 1 mol C9H8O4 |
| 1 mol C7H6O3 |
| 180.12 g C9H8O4 |
| 1 mol C9H8O4 |
theoretical yield of aspirin if acetic anhydride is the limiting reactant:
30.00_0__

17.00 g C4H6O3 ×
×
×
= 30.00 g C9H8O4
g C9H8O4
| 1 mol C4H6O3 |
| 102.09 g C4H6O3 |
| 1 mol C9H8O4 |
| 1 mol C4H6O3 |
| 180.12 g C9H8O4 |
| 1 mol C9H8O4 |
theoretical yield of aspirin:
26.09_0__
The smaller of the two masses determined in Steps 1 and 2 (26.09 g) is the theoretical yield.
g C9H8O4

actual yield of aspirin:
22.36_0__
The actual yield is given in the problem as 22.36 g.
g C9H8O4

percent yield:
85.70_0__
× 100% = 85.70%
%

| 22.36 g obtained |
| 26.09 g possible |
1.5-11. Reaction Table Lecture
Reaction Table Lecture
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•View the video full screen in another window.
-
•View the video in text format by scrolling down.
1.5-12. Lines of a Reaction Table
Reaction tables have three rows (initial, Δ, and final) and a column for each reactant and product in the chemical equation.
-
1initial: The initial line consists of the number of moles of each ingredient present before the reaction begins. Only the reactants are mixed in most reactions, so the entries under the products are zero in most reaction tables.
-
2Δ: The delta (change) line shows how many moles of each reactant disappears and how many moles of each product are produced. All calculations on this line are based on the assumption that all of the limiting reactant disappears. The entries of all products are positive because they form during the reaction, but those of all reactants are negative because they disappear during the reaction.
-
3final: The final line is the sum of the initial and delta lines and represents the final composition of the reaction mixture.
1.5-13. Reaction Table from Mass Exercise
Exercise 1.26:
Reaction tables are completed with either moles or concentrations, not with masses. However, initial amounts are often given as masses. In these cases, convert the masses into moles and proceed as in the previous example.
Construct the reaction table to determine the final masses of all substances remaining in the complete reaction of 10.00 g each of NH3 and O2. Report the final masses to the nearest 0.01 g.
| 4 NH3 | + | 5 O2 | → | 4 NO | + | 6 H2O | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| initial |
0.5872_0__
10.00 g NH3 ×
|
+ |
0.3125_0__
10.00 g O2 ×
|
→ |
0_0__
Initially there is no product so this amount is zero.
|
+ |
0_0__
Initially there is no product so this amount is zero.
|
mol | ||||||
| Δ |
-0.2500_0_4_
0.3125 mol O2 ×
|
-0.3125_0__
All 0.3125 moles of oxygen disappear. The fact that they disappear is designated by a minus sign.
|
+0.2500_0_4_
0.3125 mol O+2 ×
Since the NO is a product, it is being produced during the reaction, so the Δ line entry under NO is +0.2500 mol. |
+0.3750_0_4_
0.3125 mol O2 ×
Since the H2O is a product, it is being produced during the reaction, so the Δ line entry under H2O is +0.3750 mol. |
mol | |||||||||
| final |
0.3372_0__
0.5871 mol initially – 0.2500 mol react = 0.3372 mol at completion
|
0.0 _0__
0.3125 mol initially – 0.3125 mol react = 0 mol at completion
|
0.2500 _0__4
0 mol initially + 0.2500 mol form = 0.2500 mol at completion
|
0.3750_0__4
0 mol initially + 0.3750 mol form = 0.3750 mol at completion
|
mol | |||||||||
| mass |
5.74_0__
0.3372 mol NH3 ×
|
0.0_0__
None of the limiting reactant remains.
|
7.50_0_3_
0.2500 mol NO ×
|
6.76_0__
0.3750 mol H2O ×
|
g |
