Chapter 2 – Solutions
Introduction
Solutions are all around us. Our atmosphere is a solution of gases in gases, carbonated beverages are solutions of gases in liquids, sweetened drinks are solutions of solids in liquids, and solder is a solution of solids in solids. Reactions are normally carried out in solutions of gases or liquids because the particles in these solutions are free to move and to collide. In this chapter, we define several terms relevant to the study of solutions and discuss some solution properties.2.1. Concentration Units
Introduction
The properties of a solution depend upon the relative amounts of solvent and solute(s), which is given by the solute concentration in the solution. A concentrated solution is one in which the concentration of a solute is relatively large, while a dilute solution is one in which the solute concentrations are relatively low. However, the terms 'concentrated' and 'dilute' used in this manner are not quantitative. In this section, we present several different ways of reporting the concentrations of solutions in a quantitative manner.Objectives
-
•Determine the concentration of a solution from the amount of solute and the amount of solution or solvent.
-
•Use the definition of a concentration unit to convert between the amount of solute and the amount of solution or solvent.
-
•Prepare a solution of known molarity.
-
•Use and understand the meaning of the prefixes m (milli), µ (micro) and n (nano).
2.1-1. Definitions
A solution consists of a solvent and one or more solutes.
-
•A solution is a homogeneous mixture consisting of a solvent and one or more solutes. A homogeneous mixture is one whose composition is the same throughout. For example, sugar dissolves in water to make a homogeneous mixture in which the sugar concentration (sweetness) is the same throughout, so the mixture is a solution. Mixing water and oil forms a mixture whose composition varies from pure water to pure oil, so this mixture is heterogeneous and not a solution.
-
•The solvent is that substance that dictates the phase of the solution. If a liquid is present, it is usually the solvent. This course focuses on aqueous solutions, which are solutions in which water serves as the solvent.
-
•A solute is one of the substances that is dissolved in the solvent. Solutes of aqueous solutions can be solid (a sugar solution), liquid (alcoholic beverages contain liquid ethanol in water), and/or gas (carbonated beverages contain CO2 in water).
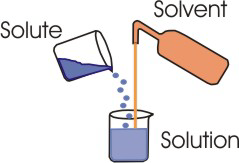
Figure 2.1: Components of a Solution
A solution consists of a solvent and at least one solute. Almost all of the solutions considered in this course are aqueous solutions, which are solutions in which water is the solvent.
2.1-2. Molarity (M)
The molarity (M) of a solute is the number of moles of the solute in one liter of solution or the number of millimoles of solute in one milliliter of solution.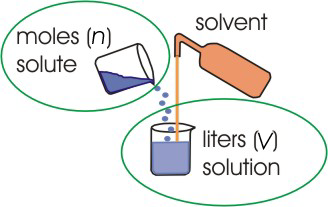
Figure 2.2: Molarity
Molarity relates moles of solute to the volume of solution.
M =
=
=
for n, the number of moles:
Alternatively, we can use the units of molarity and the factor-label method to determine the number of moles.
If V is given in milliliters, then MV is millimoles of solute. We will frequently use millimoles because volumes in a chemistry laboratory are most often given in milliliters.
We can also solve Equation 2.1| moles of solute |
| liters of solution |
| n |
| V |
| mmoles of solute |
| mL of solution |
M =
=
=
for the volume of solution to determine what volume of solution contains a given number of moles of solute:
Or, using the factor-label method,
| moles of solute |
| liters of solution |
| n |
| V |
| mmoles of solute |
| mL of solution |
2.1-3. Preparing a Solution of Known Molarity
The denominator of molarity is the volume of the solution, not the volume of solvent. Thus, a solution of known molarity must be made by adjusting the volume after the solute and solvent have been thoroughly mixed. This is done with a volumetric flask of the appropriate volume (Figure 2.3) as follows.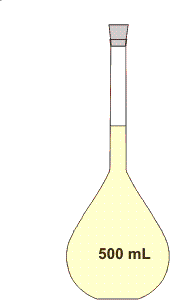
Figure 2.3: A 500-mL Volumetric Flask
-
1Select a volumetric flask of the appropriate volume and determine the amount of solute that will be required. The flask in Figure 2.3 would be used to prepare 500 mL of solution.
-
2Add solvent to the volumetric flask until it is about half full.
-
3Add the required amount of solute and swirl the mixture until the solute has dissolved
-
4Add solvent to the flask up to the fill line of the flask.
-
5Invert the flask several times to assure homogeneity.
2.1-4. Preparing a Solution Exercise
Exercise 2.1:
How many mmoles of K2HPO4 are required to prepare 350. mL of 0.0865 M K2HPO4?
30.3_0__
or
(0.0303 mol)(1000 mmol/mol) = 30.3 mmol mmol
350. mL of solution ×
= 30.3 mmol
| 0.0865 mmol K2HPO4 |
| 1 mL solution |
or
0.350 L of solution ×
= 0.0303 mol
| 0.0865 mol K2HPO4 |
| 1 L solution |
(0.0303 mol)(1000 mmol/mol) = 30.3 mmol mmol
How many grams of K2HPO4 (Mm = 174.17 g/mol) must be dissolved to make the solution?
5.27_0__

30.3 mmol ×
×
= 5.27 g K2HPO4
g
| 174.17 mg K2HPO4 |
| 1 mmol K2HPO4 |
| 1 g |
| 1000 mg |
Molarity is the number of moles of solute per liter of solution not solvent, so the K2HPO4 would be dissolved in less than 350 mL of water (~250 mL). Water would then be added to adjust the volume of the resulting solution to 350 mL.
How many milliliters of the 0.0865 M solution of K2HPO4 are required to deliver 3.50 mmoles of K1+ ions?
V =
20.2_0__

3.50 mmol K1+ ×
×
= 20.2 mL solution
mL
| 1 mmol K2HPO4 |
| 2 mmol K1+ |
| 1 mL solution |
| 0.0865 mmol K2HPO4 |
2.1-5. Molarity to Solute Mass Exercise
Exercise 2.2:
Ocean water is typically 0.53 M in chloride ion. How many grams of chloride ion are contained in 500. mL of ocean water?
mass =
9.4_0__

500. mL solution ×
×
×
= 9.4 g Cl1–
g Cl1–
| 1 L solution |
| 1000 mL solution |
| 0.53 mol Cl1– |
| 1 L solution |
| 35.5 g Cl1– |
| 1 mol Cl1– |
2.1-6. Molarity of Ions Exercise
Exercise 2.3:
Ba(OH)2 is a strong electrolyte. What are the ion concentrations in a solution prepared by dissolving 0.210 g of Ba(OH)2 in enough water to make 450. mL of solution?
The molarity of the Ba(OH)2 solution is:
0.00272_0__

n = 210 mg Ba(OH)2 ×
= 1.23 mmolBa(OH)2
| 1 mmol Ba(OH)2 |
| 171.3 mg Ba(OH)2 |
M =
=
= 0.00272 M
M
| n |
| V |
| 1.23 mmol Ba(OH)2 |
| 450 mL solution |
The ion concentrations are:


[OH1−]
=
0.00544_0__
There are two OH1– for each Ba(OH)2.
M
[Ba2+]
=
0.00272_0__
There is one Ba2+ for each Ba(OH)2.
M
The number of millimoles of OH1– in 275 mL of solution is:
1.50_0_3_

275 mL solution ×
= 1.50 mmol OH1–
mmol
| 0.00545 mmol OH1– |
| 1 mL solution |
The number of milliliters of solution required to deliver 0.300 mmol of Ba2+ is:
110._0_3_

0.300 mmol Ba2+ ×
= 110 mL solution
mL
| 1 mL solution |
| 0.00272 mmol Ba2+ |
2.1-7. Common Prefixes
1 M solutions are considered fairly concentrated, and most of the solutions encountered in the chemistry laboratory are much less concentrated. Indeed, some processes require only very dilute concentrations. For example, the maximum allowed level of mercury in drinking water is 0.000002 M, and a testosterone level of only 0.00000001 M initiates puberty in human males. Prefixes are used to avoid the preceding zeros or exponents when expressing these very dilute solutions.| Unit | Symbol | Value | |
|---|---|---|---|
| millimolar | mM | 10–3 M | 1 mmol·L–1 |
| micromolar | µM | 10–6 M | 1 µmol·L–1 |
| nanomolar | nM | 10–9 M | 1 nmol·L–1 |
Table 2.1: Common Prefixes
Thus, the maximum allowed level of mercury in drinking water is 2 × 10–6 M = 2 µM, and the testosterone level that initiates puberty is 10 × 10–9 M = 10 nM.
2.1-8. Using Prefixes Exercise
Exercise 2.4:
How many micrograms of testosterone (C19H28O2, Mm = 288 g/mol) are in the blood (5.7 liters) of a person if the testosterone concentration is 12.5 nM?
mass =
21_0__

5.7 L blood ×
×
×
= 21 µg C19H28O2
µg testosterone
| 12.5 e−09 mol C19H28O2 |
| 1 L blood |
| 288 g C19H28O2 |
| 1 mol C19H28O2 |
| 1e+06 µg C19H28O2 |
| 1 g C19H28O2 |
2.1-9. Mole Fraction (X)
The mole fraction (X) of a substance in a solution is the number of the moles of that substance divided by the total number of moles of all substances (solutes and solvent) in solution. Because all of the substances comprise the whole mixture, the sum of all mole fractions (including the solvent) must equal one; i.e.,| XA | |
 | |
| A |
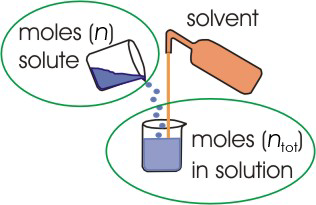
Figure 2.4: Mole Fraction
The mole fraction of A equals the number of moles of A divided by the total number of moles of substances in the solution.
2.1-10. Mole Fraction Exercise
Exercise 2.5:
A sample of the alloy known as "yellow brass" is found to be 67.00% Cu and 33.00% Zn by mass. What are the mole fractions of Cu and Zn in the alloy?
Exactly 100 g of alloy contains:
1.054_0__

67.00 g Cu ×
= 1.054 mol Cu
mol Cu
| 1 mol Cu |
| 63.546 g Cu |
0.5047_0__

33.00 g Zn ×
= 0.5047 mol Zn
mol Zn
| 1 mol Zn |
| 65.39 g Zn |
1.559_0__
1.054 mol Cu + 0.5047 mol Zn = 1.559 mol total
mol total in mixture

The mol fractions are
XCu =
0.6763_0__
= 0.6763

| 1.0544 mol Cu |
| 1.5590 mol total |
XZn =
0.3237_0__
= 0.3237
Alternatively, XZn = 1.0000 – XCu = 1.0000 – 0.6763 = 0.3237
| 0.50466 mol Zn |
| 1.5590 mol total |
Alternatively, XZn = 1.0000 – XCu = 1.0000 – 0.6763 = 0.3237
2.1-11. Mass Fraction (%, ppt, ppm)
The mass fraction relates the mass of a solute to the mass of the solution. It is commonly used for solutions where the solvent is not clearly defined.
Figure 2.5: Mass Fraction
The mass fraction relates the mass of a solute to the mass of the solution.
2.1-12. Mass Fraction Multipliers
Mass fractions represent a part of the whole, so they are always less than one. Indeed, mass fractions in dilute solutions can be so small that they are multiplied by powers of ten to eliminate the preceding zeros (see Table 2.2). Thus,-
•a mass fraction of 0.012 would be reported as (0.012)(100%) = 1.2%
-
•a mass fraction of 1.2 × 10–8 would be reported as (1.2 × 10–8)(109 ppb) = 12 ppb.
| Name | Multiplier | Useful Units | ||
|---|---|---|---|---|
| mass fraction | 1 |
|
||
| mass percent (%) | 100 |
|
||
| parts per thousand (ppT) | 1000 |
|
||
| parts per million (ppm) | 106 |
|
||
| parts per billion (ppb) | 109 |
|
Table 2.2: Common Multipliers Used with Mass Fraction
2.1-13. Mass Fraction Exercise
Exercise 2.6:
A mixture contains 6.0 g N2, 16.0 g O2 and 2.0 g He.
What are the mass fraction, mass percent, and mole fraction of each gas?
What are the mass fraction, mass percent, and mole fraction of each gas?
Mass Fractions
Total mass =
24.0_0__1
6.0 g N2 + 16.0 g O2 + 2.0 g He = 24.0 g total.
g

Mass fraction of N2 =
.25_0__
= 0.25

| 6.0 g N2 |
| 24.0 g total |
Mass fraction of O2 =
.667_0__
= 0.667

| 16.0 g O2 |
| 24.0 g total |
Mass fraction of He =
.083_0__
= 0.083

| 2.0 g He |
| 24.0 g total |
Mass Percents
Mass percent of N2 =
25_0__
Multiply the mass fraction of nitrogen by 100
%

Mass percent of O2 =
66.7_0__
Multiply the mass fraction of oxygen by 100
%

Mass percent of He =
8.3_0__
Multiply the mass fraction of helium by 100
%

Moles
Moles of N2 =
.21_0__

6.0 g N2 =
= 0.21 mol N2
mol
| 1 mol N2 |
| 28.0 g N2 |
Moles of O2 =
.500_0_3_

16.0 g O2 =
= 0.500 mol O2
mol
| 1 mol O2 |
| 32.0 g O2 |
Moles of He =
.50_0_2_

2.0 g He =
= 0.50 mol He
mol
| 1 mol He |
| 4.0 g He |
Total moles =
1.21_0__
0.21 mol N2 + 0.50 mol O2 + 0.50 mol He = 1.21 mol total
mol

Mole Fractions
XN2 =
.17_0__
= 0.17

| 0.21 mol N2 |
| 1.21 mol total |
XO2 =
.412_0_3_
= 0.412

| 0.500 mol O2 |
| 1.21 mol total |
XHe =
.41_0__
= 0.41

| 0.50 mol Ne |
| 1.21 mol total |
2.1-14. Molality (m)
The molality (m) of a solute is the number of moles of that solute per kilogram of solvent.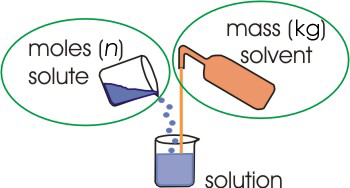
Figure 2.6: Molality
Molality relates the moles of solute to the mass of solvent.
2.1-15. Molality Exercise
Exercise 2.7:
A solution is prepared by mixing 3.75 g of glucose (C6H12O6, Mm = 180.2 g/mol) and 25.0 g of water. What is the molality of the resulting glucose solution?
moles of glucose in solution
0.0208_0__

3.75 g ×
= 0.0208
mol C6H12O6
| 1 mol |
| 180.2 g |
kilograms of solvent present in solution
0.0250_0_3_
25.0 grams is 0.0250 kg.
kg H2O

the molality of the solution
0.832_0__
= 0.832 m
m

| 0.0208 mol glucose |
| 0.0250 kg solvent |
2.2 Changing Concentrations Units
Introduction
It is sometimes necessary to change the units of concentration. This routine procedure is most often done when the concentration of a stock solution is given in units that are not convenient for a particular experiment. The procedure presented here entails converting the units of the numerator and denominator of the given concentration to those of the desired concentration and then dividing.Objectives
-
•Convert between different concentration units.
2.2-1. Converting Concentration Units
To change concentration units, convert the numerator and denominator separately.
-
1Convert the given numerator into the numerator of the desired unit.
-
2Convert the given denominator into the denominator of the desired unit.
-
3Divide the result of step 1 by that of step 2 to obtain the desired concentration unit.
| molarity | mass fraction | mole fraction | molality | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
To convert between any of the above you need only some combination of the molar masses of solute and/or solvent, and/or the density of the solution.
| Conversion | Requires |
|---|---|
| mol solute ↔ mass solute | molar mass of the solute |
| liters solution ↔ mass solution | density of solution |
| liters solution ↔ mol solute + mol solvent | density of solution, molar masses of solute and solvent |
| liters solution ↔ kg solvent | solution density, molar mass of solute |
| mass solution ↔ mol solute + mol solvent | molar masses of solute and solvent |
| mass solution ↔ kg solvent | molar mass of solute |
| mol solute + mol solvent |
molar masses of solute and solvent |
Table 2.3: Converting Concentration Units
2.2-2. Molarity to Mass Percent Exercise
Exercise 2.8:
A solution of concentrated sulfuric acid is 18.00 M and has a density of 1.839 g/cm3. What is the mass percent of H2SO4 in the concentrated acid solution? Molar mass of sulfuric acid = 98.08 g/mol.
The given units are molarity, while the desired units are mass fraction, which must be multiplied by 100 to obtain mass percent. Molarity has units of (mol solute)/(L solution), while mass fraction has units of (mass solute)/(mass solution). Thus, we must make the following conversions.
-
•numerator: 18.00 mol H2SO4 yields ↔ x grams H2SO4
-
•denominator: 1 L solution yields ↔ y grams solution
Convert the given numerator into the desired numerator.
18.00 mol H2SO4 =
1765_0__

18.00 mol H2SO4 ×
= 1765 g H2SO4
g H2SO4
| 98.08 g H2SO4 |
| 1 mol H2SO4 |
Convert the denominator of the given concentration units into those of the desired concentration units.
1 L solution =
1839_0__

1 L soln ×
×
= 1839 g soln
g solution
| 1000 mL soln |
| 1 L soln |
| 1.839 g soln |
| 1 mL soln |
The mass fraction of H2SO4 in the solution =
0.9600_0_4_

X =
= 0.9600
| 1.76544e+03 g H2SO4 |
| 1.839e+03 g soln |
The mass percent of H2SO4 in the solution =
96.00_0_4_
mass percent = (mass fraction)(100%) = (0.9600)(100%) = 96.00%
%

2.2-3. Molarity to Molality Exercise
Exercise 2.9:
Concentrated sulfuric acid is 18.00 M and has a density of 1.839 g/cm3. What is the molality of H2SO4 in the concentrated acid solution?
The given units are molarity, while the desired units are molality. Molarity has units of (mol solute)/(L solution), while molality has units of (mol solute)/(kg solvent). Thus, we must make the following conversions:
-
•numerator: 18.00 mol H2SO4 → 18.00 mol H2SO4
-
•denominator: 1 L solution → y kilograms solvent
The numerators are the same (18.00 mol), so we need only change the denominator and then divide.
1 L solution contains
.074_0__
From the previous part, we know that 1839 g soln contains 1765 g H2SO4. Thus, the solution must contain 1839 – 1765 = 74 g water. The denominator must be kilograms, so the answer is 0.074 kg.
kg solvent

Divide the numerator by the denominator to obtain molality:
240_0_2_
= 2.4e+02 m
m

| 18.00 mol H2SO4 |
| 0.074 kg solvent |
2.2-4. ppm to Molarity Exercise
Exercise 2.10:
What is the molarity of fluoride ion in drinking water that is 7.0 ppm F1–?
The given units are ppm, (grams solute)/(106 g solution), while the desired units are molarity, (mol solute)/(L solution). Thus, the following conversions are required.
-
•numerator: 7.0 g F1– → x mol F1–
-
•denominator: 106 g solution → y liters of solution
Convert the given numerator into the desired numerator.
7.0 g F1– =
0.37_0_2_
The molar mass of fluoride ion is 19.0 g/mol, so 
7.0 g F1− =
= 0.37 mol.
mol F1–
| 1 mol F1− |
| 19.0 g F1− |
Next, convert the denominator of the given concentration into that of the desired concentration. This solution is very dilute, so you can assume that the density of the solution is the same as the solvent (1.0 g/mL).
106 g solution =
1e3_0_2_

106 g solution ×
×
= 1.0e3 L soln
L solution
| 1 mL soln |
| 1.0 g soln |
| 1 L soln |
| 1000 mL soln |
Finally, divide the two to obtain the desired concentration units.
= 3.7e−04 M
M

[F1−]
=
3.7e-4_0__
| 0.37 mol F1− |
| 1e3 L soln |
2.2-5. Mass Percent to Molarity Exercise
Exercise 2.11:
What is the molarity of a 30.0% sulfuric acid solution if its density is 1.218 g/mL?
-
•numerator: 30.0 g H2SO4 → x mol H2SO4
-
•denominator: 100 g soln → y L soln
Convert the given numerator into the desired numerator.
30.0 g H2SO4 =
0.306_0__
The molar mass of H2SO4 is 98.08 g/mol, so 
30.0 g H2SO4 ×
= 0.306 mol H2SO4.
mol H2SO4
| 1 mol H2SO4 |
| 98.08 g H2SO4 |
Next, convert the denominator of the given concentration into that of the desired concentration.
100 g solution =
0.08210_0_4_

100 g soln ×
×
= 0.08210 L soln
L solution
| 1 mL soln |
| 1.218 g soln |
| 1 L soln |
| 1000 mL soln |
Finally, divide the two to obtain the desired concentration units.
= 3.73 M
M

[H2SO4]
=
3.73_0__
| 0.306 mol H2SO4 |
| 0.08210 L soln |
2.3 Dilutions
Introduction
Stock solutions are often fairly concentrated and must be diluted before they are used. In this section, we show how to make a solution of known volume and molarity from a more concentrated stock solution.Objectives
-
•Calculate the concentration of a solution after dilution.
-
•Prepare a dilute solution of known concentration from a more concentrated solution.
2.3-1. Dilution Lecture
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•View the video full screen in another window.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
2.3-2. Equations of Dilution
The amount of solute does not change with the addition of solvent, so we can write the following: where C is any concentration that indicates the amount of solute per unit volume of solution. Therefore, C can be molarity or g/mL, but not molality or mass percent. We solve Equation 2.5 for the final concentration, Cf to obtain the following where the ratio Vi/Vf is called the dilution factor. Thus, the final concentration equals the initial concentration times a dilution factor. If a solution is diluted successively several times, then the final concentration equals the initial concentration times the product of all of the successive dilution factors as shown in Equation 2.7.2.3-3. Molarity after Dilution Exercise
Exercise 2.12:
What is the molarity of sulfuric acid in a solution prepared by adding 30.0 mL of 18.0 M H2SO4 to enough water to make 500. mL of solution?
concentration =
1.08_0__

Cf = 18.0 M ×
= 1.08 M
M H2SO4
| 30.0 mL |
| 500. mL |
2.3-4. Volume Required for Dilution Exercise
Exercise 2.13:
How many mL of 18.0 M H2SO4 are required to prepare 300. mL of 1.50 M H2SO4?
volume of 18.0 M H2SO4 =
25_0_3_
The question asks for the initial volume given that Ci = 18.0 M; Cf = 1.50 M; and Vf = 300. mL.

Vi = 300. mL ×
= 25.0 mL
mL H2SO4
| 1.50 M |
| 18.0 M |
2.3-5. Concentration After Successive Dilutions Exercise
Exercise 2.14:

Solution A is prepared by diluting 20.0 mL of a stock 0.100 M HCl solution to 50.0 mL. Solution B is prepared by diluting 10.0 mL of solution A to 75.0 mL. Solution C is made by diluting 20.0 mL of solution B to 250.0 mL. What is the concentration of HCl in solution C? Note that the concentration is expressed as millimolar.
[HCl]
in solution C =
0.427_0__
[HCl] = 100. mM ×
×
×
= 0.427 mM
mM
| 20.0 mL |
| 50.0 mL |
| 10.0 mL |
| 75.0 mL |
| 20.0 mL |
| 250.0 mL |
2.3-6. Concentration of Initial Solution Exercise
Exercise 2.15:
50.00 mL of an unknown solution A is diluted to 500.00 mL to make solution B. 25.00 mL of solution B is diluted to 750.00 mL to make solution C. 15.00 mL of solution C is diluted to 1000.00 mL. What is the concentration of solution A, if the concentration of the final solution is 1.47 µM?
product of all dilution factors =
5.000e-5_0_4_

DF =
×
×
| 50.00 mL |
| 500.00 mL |
| 25.00 mL |
| 750.00 mL |
| 15.00 mL |
| 1000.00 mL |
concentration of solution A =
0.0294_0__

CA =
=
= 0.0294 M
M
| Cf |
| DF |
| 1.47e−06 M |
| 5.000e−05 |
2.4 Determining Concentrations
Introduction
Analyzing solutions to determine their concentration is an important part of analytical chemistry. In this section, we discuss two important methods used to carry out such an analysis: spectrometry and titration.Objectives
-
•Use a color wheel to determine a complementary color.
-
•Use Beer's Law to determine the molarity of a solution.
-
•Determine the volume of one reactant that reacts with another reactant of known volume.
-
•Determine the limiting reactant from a balanced chemical equation and the concentrations and volumes of the reactants.
-
•Determine the concentrations of the excess reactants.
2.4-1. Complementary Colors
White light is the result of all visible colors. When white light shines on a colored substance, however, some of the colors are absorbed. Those colors that are not absorbed can be either reflected or transmitted to the eye. We perceive this reflected or transmitted portion as the color of the substance. Consequently, the characteristic color of a material is not the color of light that it absorbs; rather it is the mixture of the remaining, unabsorbed colors that are observed. In other words, it appears as its complementary color. The approximate relationship between observed and absorbed colors is summarized in a color wheel as shown in Figure 2.7. For example, a solution appears orange because it absorbs blue light. Thus, when white light shines on the solution, the blue portion of the spectrum is absorbed by the solution, which leaves only the orange portion to be detected by your eyes.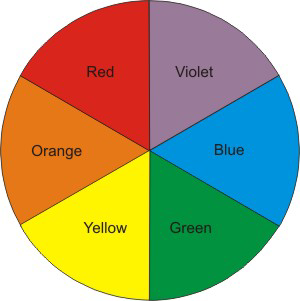
Figure 2.7: Color Wheel
Complementary colors are opposite one another in a color wheel, so orange is the complement of blue.
2.4-2. Spectrometry
Spectrometry, measuring the amount of light that a solute absorbs at some wavelength, is a convenient way to determine the concentration of a solute in a solution. The amount of light that is absorbed by the sample is called the absorbance (A) of the sample. Consider the experiment shown in Figure 2.8 below. Orange light of intensity Io enters the cell, where some of it is absorbed by the blue solution, so the outgoing intensity I, is less than the initial Io.
Figure 2.8: Absorbance and Beer's Law
Orange light is absorbed by a blue solution. The amount of light that is absorbed by the solution is called the absorbance (A), which is defined as –log(I/Io). The absorbance depends upon the concentration of the absorbing substance (c), the distance the light travels through the sample (l), and the molar absorptivity of the solute at the wavelength of the light (ε) as given by Beer's law.
-
•how strongly the solute absorbs at the wavelength of light used in the experiment, which is known as the molar absorptivity (ε, epsilon);
-
•the concentration of the solute (c); and
-
•the path length of the light through the solution (l).
2.4-3. Determining an Unknown Concentration
The following procedure is used to determine an unknown concentration in a solution:-
1Determine a good wavelength of light to use. The light should be absorbed by the solute to be determined, so it should be the complement of the color of the solution. The complement can be found as the color opposite the observed color on a color wheel. The light should not be absorbed by the rest of the solution, but the effect of the rest of the solution can be determined by measuring the absorbance of a blank. The blank should mimic the solution to be measured in all aspects except the presence of the solute to be measured. The absorbance of the blank is then subtracted from that of the sample to get a measurement of just the solute's absorbance.
-
2Measure the absorbance of a standard solution, which is simply a solution in which the concentration of the solute being measured is accurately known. The molar absorptivity of the solute can be determined from the measured absorbance, the known concentration, and the path length of the cell.
-
3Measure the absorbance of the sample. The unknown concentration can be determined from the measured absorbance, the molar absorptivity determined in step 2, and the known path length of the cell.
2.4-4. Determining Concentration Exercise
Thank you for your patience as this section undergoes re-construction.2.4-5. Titrations
Spectrometry is an easy way to determine an unknown concentration only if the solute absorbs light at a convenient wavelength (usually one in the visible). The concentration of a solute can also be determined by measuring the stoichiometric amount of a solution of known concentration required to react with the unknown solute. This method is called titration. The known solution, whose volume is to be determined, is called the titrant, while the solute being analyzed is the analyte. The point at which the titrant and analyte are in stoichiometric amounts is called the equivalence point. The equivalence point is usually approximated by an end point, which is the point at which an indicator undergoes a color change.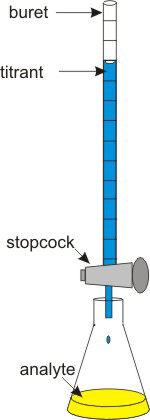
Figure 2.9: Titration Apparatus
2.4-6. Titration Method
Acid-base titrations are very common in the chemistry lab. The net chemical equation for the reaction of a strong acid and a strong base is:H3O1+ + OH1− → 2 H2O
2.4-7. Titration Exercise
Thank you for your patience as this section undergoes re-construction.2.4-8. Precipitation Reactions
Solubility rules can help you determine the precipitate.
-
1Use the solubility rules to decide upon a good reactant.
-
2Add an excess of the reactant to a known volume of the solution to be analyzed.
-
3Filter the solution to separate the precipitate from the solution. Add more reactant to the remaining solution to be certain no more precipitate forms.
-
4Dry and weigh the precipitate then determine the number of moles of precipitate that were produced.
-
5Use the results of step 4 to determine the number of moles of the solute that must have reacted.
-
6Determine the concentration of the original solution from the number of moles of solute present (step 5) and the original volume.
| Rule 1 | Compounds of NH41+ and group 1A metal ions are soluble. |
| Rule 2 | Compounds of NO31–, ClO41–, ClO31– and C2H3O21– are soluble. |
| Rule 3 | Compounds of Cl1–, Br1–, and I1– are soluble except those of Ag1+, Cu1+, Tl1+, Hg22+,and Pb2+. |
| Rule 4 | Compounds of SO42– are soluble except those of Ca2+, Sr2+, Ba2+, and Pb2+ |
| Rule 5 | Most other ionic compounds are insoluble. |
Table 2.4: Solubility Rules
Solubility rules for ionic compounds in water.
Solubility rules for ionic compounds in water.
2.4-9. Precipitation Exercise
Exercise 2.18:
What is the concentration of Ag1+ ions in a solution if addition of excess PO43– ions to 25.00 mL of the solution produced 163.2 mg of Ag3PO4 (Mm = 418.6 g/mol)?
The net ionic equation is: 3 Ag1+ + PO43– → Ag3PO4
The number of millimoles of Ag3PO4 produced =
0.3899_0__

163.2 mg Ag3PO4 ×
= 0.3899 mmol Ag3PO4
mmol
| 1 mmol Ag3PO4 |
| 418.6 mg Ag3PO4 |
The number of millimoles of Ag1+ required =
1.170_0_4_

0.3899 mmol Ag3PO4 ×
= 1.170 mmol Ag1+
mmol
| 3 mmol Ag1+ |
| 1 mmol Ag3PO4 |
The concentration of Ag1+ in the original solution =
0.04678_0__
1.1696 mmol Ag1+ was in 25.00 mL of solution.

[Ag1+] =
= 0.04678 M
M
| 1.1696 mmol Ag1+ |
| 25.0 mL solution |
2.5 Colligative Properties
Introduction
The properties of a solution depend upon the concentrations of the solutes. Indeed, some solution properties depend only upon the concentration of particles in solution and not upon the identity of those particles. These properties are called colligative properties. In this section, we discuss the following colligative properties.-
•vapor pressure
-
•boiling point
-
•freezing point
-
•osmotic pressure
Objectives
-
•Determine the van't Hoff factor (i) for a compound.
-
•Convert a molarity or molality into a colligative molarity or colligative molality.
-
•Calculate the boiling point and melting point of a solution given its colligative molality and the boiling elevation and freezing point depression constants.
-
•Describe the causes of vapor pressure lowering at the molecular level.
-
•Calculate the vapor pressure of a solution given the mole fraction of the solute and the vapor pressure of the solvent.
-
•Describe osmosis at the molecular level.
-
•Determine the osmotic pressure of a solution of known concentration.
-
•Explain why osmosis is important.
2.5-1. van't Hoff Factor and Colligative Concentrations
Colligative properties depend upon the concentration of particles in solution, which is different than the solute concentration when the solute is ionic and dissociates in water. The solution concentration is converted to a concentration of particles with the van't Hoff factor (i), which is the number of moles of particles produced when one mole of solute dissolves. For example, i = 3 for CaCl2 because dissolving one mole of CaCl2 produces three moles of ions: CaCl2 → Ca2+ + 2 Cl1–. The total particle concentration is called the colligative concentration. It is equal to the solute concentration times its van't Hoff factor. The following equations define the colligative molarity and colligative molality.2.5-2. van't Hoff Exercise
Exercise 2.19:
What is the van't Hoff factor for each of the following?
CaSO4:
i =
2_0__
CaSO4 → Ca2+ + SO42–

CH3OH:
i =
1_0__
CH3OH is a nonelectrolyte.

NH4ClO:
i =
2_0__
NH4ClO → NH41+ + ClO1–

Ba(OH)2:
i =
3_0__
Ba(OH)2 → Ba2+ + 2 OH1–

HCl:
i =
2_0__
HCl → H1+ + Cl1–

SF4:
i =
1_0__
SF4 is a nonelectrolyte.

2.5-3. Colligative Molality Exercise
Exercise 2.20:
Determine the colligative molarity of each of the following solutions.
| Solution | i | Mc |
|---|---|---|
| 0.080 M K3PO4 |
4_0__
K3PO4 → 3 K1+ + PO43–
|
0.32_0__
Mc = iM
|
| 0.042 M C6H12O6 |
1_0__
C6H12O6 is a nonelectrolyte.
|
0.042_0__
Mc = iM
|
2.5-4. Phase Diagram
Figure 2.10 shows the phase diagrams of a pure substance and of a solution in which the substance is the solvent. The two diagrams are identical except for the region in blue, which is either a solid or gas in the pure substance but is all liquid in the solvent. Thus, the phase diagram of the solvent differs from that of the pure substance in three ways:-
•The vapor pressure is lowered by ΔP at every temperature.
-
•The boiling point is elevated (raised) by ΔTb.
-
•The freezing point is depressed (lowered) by ΔTf.
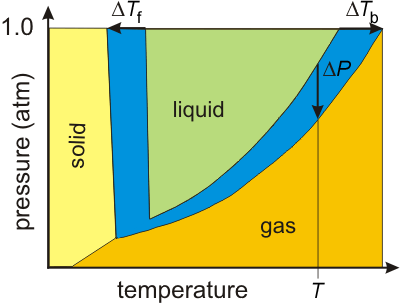
Figure 2.10: Phase diagrams of a solvent and a solution of the solvent.
The solvent is liquid only in the green region, while the solution is liquid in both the green and blue regions; i.e., the blue region shows the extent to which the liquid state is expanded due to the presence of the solute particles.
2.5-5. Vapor Pressure Lowering
The vapor pressure of a solution is less than that of the pure solvent.
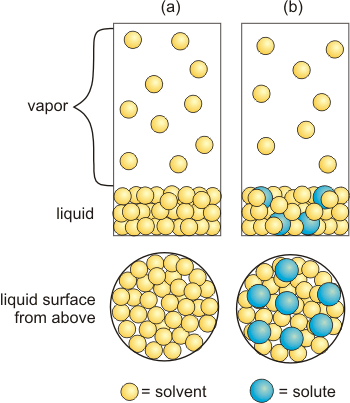
Figure 2.11: Vapor Pressure Lowering
(a) Solvent: All of the surface sites are occupied by solvent molecules, which produces ten molecules in the vapor. (b) Solution: The mole fraction of the solute in the solution is ~0.2, so nonvolatile solute particles (blue spheres) occupy ~20% of the surface sites, which reduces the vapor pressure by ~20% as shown by the presence of only eight molecules in the vapor.
2.5-6. Vapor Pressure of Water
We will have made frequent use of the vapor pressure of water. The vapor pressure at 5 °C increments can be found in Table 2.5 and in the Resources.| T (°C) | P° (torr) | T (°C) | P° (torr) | |
|---|---|---|---|---|
| 0 | 4.6 | 50 | 92.5 | |
| 5 | 6.5 | 55 | 118.0 | |
| 10 | 9.2 | 60 | 149.9 | |
| 15 | 12.8 | 65 | 187.5 | |
| 20 | 17.5 | 70 | 233.7 | |
| 25 | 23.8 | 75 | 289.1 | |
| 30 | 31.8 | 80 | 355.1 | |
| 35 | 41.2 | 85 | 433.6 | |
| 40 | 55.3 | 90 | 525.8 | |
| 45 | 71.9 | 95 | 633.9 |
Table 2.5: Vapor Pressure of Water at Selected Temperatures
2.5-7. Vapor Pressure Lowering Exercise
Exercise 2.21:
What is the vapor pressure at 25 °C of a solution prepared by dissolving 10.0 g NaCl in 100. g of water?
1. moles of NaCl in solution:
0.171_0__

10.0 g NaCl ×
= 0.171 mol NaCl
| 1 mol NaCl |
| 58.5 g NaCl |
2. moles of solute particles in solution:
0.342_0_3_

0.171 mol NaCl ×
= 0.342 mol particles
| 2 mol particles |
| 1 mol NaCl |
3. moles of solvent particles in solution:
5.56_0__

100 g H2O ×
= 5.56 mol H2O
| 1 mol H2O |
| 18.0 g H2O |
4. moles of solute and solvent particles in solution:
5.90_0__2
0.342 mol solute particles + 5.56 mol H2O = 5.90 mol

5. mole fraction of solvent:
0.942_0__

Xsolvent ×
= 0.942
| 5.56 mol H2O |
| 5.90 mol particles |
6. vapor pressure of solvent at 25 °C (see Table 2.5):
23.8_0__
The vapor pressure of pure water is found to be 23.8 torr, from Table 2.5.
torr

7. vapor pressure of solution at 25 °C:
22.4_0__
P = (0.942)(23.8 torr) = 22.4 torr.
torr

2.5-8. Boiling Point Elevation
The normal boiling point of a liquid is the temperature at which its vapor pressure is 1 atm. Although this is the definition of the normal boiling point, it is common to refer to it as simply the boiling point. The boiling point of water is 100 °C, so its vapor pressure at 100 °C is 1 atm, but the vapor pressure of an aqueous solution is less than 1 atm at 100 °C due to vapor pressure lowering. Consequently, an aqueous solution must be heated to a higher temperature to achieve a vapor pressure of 1 atm, so the boiling point of an aqueous solution is always higher than that of pure water. This reasoning can be applied to any solution, so we conclude that the boiling point of a solution is always higher than the boiling point of the pure solvent. The amount by which the boiling point of the solvent is increased by the addition of a nonvolatile solute is known as the boiling point elevation, ΔTb, which can be determined from the following equation: kb is the boiling point elevation constant, which has units of °C·m–1 and depends on the solvent, and mc is the colligative molality of the solute. ΔTb is the amount by which the boiling point of the solvent (T°b) is raised, so the boiling point of the solution (Tb) is given as2.5-9. Freezing Point Depression
Spreading salt on icy streets and sidewalks melts the ice because solute particles reduce the freezing point of a solvent in much the same way as they reduce its vapor pressure. That is, solute particles block sites on the solid where solvent molecules might otherwise freeze, thereby reducing the rate of freezing. The amount by which the freezing point is lowered is called the freezing point depression, ΔTf, and is shown in Equation 2.14: kf is the freezing point depression constant, which has units of °C·m–1 and depends on the solvent, and mc is the colligative molality of the solute. ΔTf is the amount by which the freezing point of the solvent (T°f) is lowered, so the freezing point of the solution (Tf) is given as2.5-10. Solvent Constants
The solvent constants relevant for colligative properties are shown in Table 2.6 and in the Resources.| Solvent | Freezing Point (°C) | kf (°C·m–1) | Boiling Point (°C) | kb (°C·m–1) |
|---|---|---|---|---|
| Acetic acid | 16.6 | 3.90 | 117.9 | 3.07 |
| Benzene | 5.5 | 4.90 | 80.1 | 2.53 |
| Chloroform | –63.5 | 4.70 | 61.7 | 3.63 |
| Cyclohexane | 6.6 | 20.0 | 80.7 | 2.79 |
| Ethanol | –117.3 | 1.99 | 78.5 | 1.22 |
| para-Xylene | 11.3 | 4.30 | ||
| Water | 0.0 | 1.86 | 100.0 | 0.512 |
Table 2.6: Freezing Point Depression and Boiling Point Elevation Data
for Some Solvents
for Some Solvents
2.5-11. Antifreeze Exercise
Exercise 2.22:
Antifreeze is ethylene glycol (C2H6O2, Mm = 62.1 g/mol, d = 1.11 g/mL). What are the boiling and freezing points of an aqueous solution that is 50.% ethylene glycol by volume? Assume a density of 1.0 g/mL for water.
First, we determine the molality of the solution by assuming that water is the solvent and ethylene glycol is the solute. Thus, we need the number of kg of water and the number of moles of C2H6O2. To determine the amounts, we must first choose an amount of solution. The easiest amount is exactly 1 L of solution.
The mass of H2O in 1 L of solution =
0.50_0_2_
The solution is 50% water by volume, so 1 L solution contains 500 mL water. The density of water is 1.0 g/mL.

500 mL H2O ×
×
= 0.50 kg H2O
kg
| 1.0 g H2O |
| 1.0 mL H2O |
| 1 kg H2O |
| 1e+03 g H2O |
The number of moles of C2H6O2 in 1 L of solution =
8.94_0_3_
The solution is 50% C2H6O2, so 1 L solution contains 500 mL C2H6O2. The density of C2H6O2 is given as 1.11 g/mL.

500 mL C2H6O2 ×
×
= 8.94 mol C2H6O2
mol
| 1.11 g C2H6O2 |
| 1 mL C2H6O2 |
| 1 mol C2H6O2 |
| 62.1 g C2H6O2 |
The molality of C2H6O2 =
18_0__
= 18 m
m

| 8.94 mol C2H6O2 |
| 0.50 kg H2O |
The van't Hoff factor for C2H6O2 =
1_0__
C2H6O2 is a nonelectrolyte, so i = 1

The colligative molality of the solution =
18_0_2_
mc = im = (1)(18 m) = 18 m
m

Use Table 2.6 to determine the following for water.
1. freezing point =
0_0__
The freezing point of water is 0 °C.
°C

2. boiling point =
100_0__
The boiling point of water is 100 °C.
°C

3. freezing point depression constant =
1.86_0__
The freezing point depression constant for water is found to be 1.86, from Table 2.6.
°C/m

4. boiling point elevation constant =
0.512_0__
The boiling point elevation constant for water is found to be 0.512, from Table 2.6.
°C/m

The freezing point depression of the solution =
33_0__

ΔTf = kfmc = (1.86)(18) = 33 °C
°C
The boiling point elevation of the solution =
9.2_0__

ΔTb = kbmc = (0.512)(18) = 9.2 °C
°C
The freezing point of the solution =
-33_0__

Tf = 0.0 − 33 = −33 °C
°C
The boiling point of the solution =
109.2_0__

Tb = 100.0 + 9.2 = 109.2 °C
°C
2.5-12. Salt Exercise
Exercise 2.23:
The salt that is commonly used to melt ice on roads and sidewalks is CaCl2 (Mm = 111 g/mol). Consider a solution prepared by dissolving 62.3 g CaCl2 in 100. g of water.
molality of CaCl2 =
5.61_0__
Mm = 111 g/mol, m = 62.3 g

62.3 g CaCl2 ×
= 0.561 mol CaCl2
| 1 mol CaCl2 |
| 111 g CaCl2 |
mc =
= 5.61 m
m
| 0.561 mol CaCl2 |
| 0.100 kg H20 |
colligative molality of the solution =
16.8_0__
i = 3 for CaCl2, mc = 3(5.61) = 16.8 m
m

freezing point of the solution =
-31.3_0__
kf = 1.86 °C/m for water, so ΔTf = (1.86)(16.8) = 31.3 °C
Tf = 0.0 – 31.3 = –31.3 °C °C
Tf = 0.0 – 31.3 = –31.3 °C °C
boiling point of the solution =
108.6_0__
kb = 0.512 °C/m for water, so ΔTb = (0.512)(16.8) = 8.62 °C
Tb = 100.0 + 8.62 = 108.6 °C °C
Tb = 100.0 + 8.62 = 108.6 °C °C
mole fraction of solvent =
0.767_0_3_

100 g H2O ×
= 5.556 mol H2O
| 1 mol H2O |
| 18.0 g H2O |
ntotal = 5.556 mol H2O + 3(0.561 mol ions) = 7.24 mol
Xsolvent =
= 0.767
| 5.556 mol H2O |
| 7.24 mol particles |
vapor pressure of solvent at 20 °C =
17.5_0__
The vapor pressure of water at 20 °C is found to be 17.5 torr, from Table 2.5.
torr

vapor pressure of solution at 20 °C =
13.4_0__

P = XsolventP° = (0.767)(17.5 torr) = 13.4 torr.
torr
2.5-13. Molar Mass from Freezing Point Exercise
Exercise 2.24:
A common laboratory in general chemistry is the determination of a molar mass from the freezing point depression that it causes. In this example, we outline the procedure.
1.00 g of a non-dissociating solute is dissolved in 10.0 g of para-xylene. What is the molar mass of the solute, if the freezing point of the solution was 1.95 °C lower than that of the pure solvent? kf = 4.30 °C/m for para-xylene.
Use Equation 2.14
Use the molality and the mass of the solvent to determine the number of moles of solute in the solution:
Use the mass and number of moles of the solute to determine its molar mass:
ΔTf = kfmc = ikfm
to determine the molality of the solution:
0.453_0__

m =
=
= 0.453 m
m
| ΔTf |
| kf |
| 1.95 °C |
| 4.30 °C/m |
Use the molality and the mass of the solvent to determine the number of moles of solute in the solution:
4.53e-3_0__

0.010 kg p-xylene ×
= 4.53e−03 mol solute
mol
| 0.453 mol solute |
| 1 kg p-xylene |
Use the mass and number of moles of the solute to determine its molar mass:
221_0__
1.00 g solute is 4.53e-03 mol, so 
Mm =
= 221 g/mol
g/mol
| 1.00 g |
| 4.53e−03 mol |
2.5-14. Osmosis
Solvent molecules flow through a semipermeable membrane from dilute solutions to concentrated solutions.
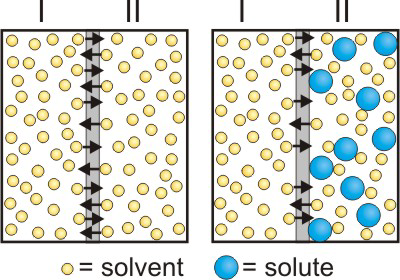
Figure 2.12: Osmosis
(a) Rate of movement through the membrane is the same in both directions because the solvent concentration is the same on both sides. (b) A solute is added to side II, so the concentration of solvent is less in side II than in side I. Consequently, the rate of solvent motion I → II is greater than II → I.
2.5-15. Osmotic Pressure
Osmotic pressure depends on colligative molarity.
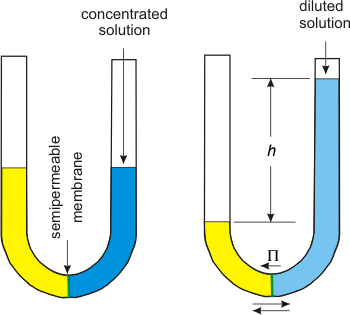
Figure 2.13: Osmotic Pressure
Solvent molecules penetrate the semipermeable membrane, but solute molecules do not. Thus, there is a net flow of water molecules
into the side with more solute.
2.5-16. Osmotic Pressure of Sea Water Exercise
Exercise 2.25:
What is the osmotic pressure developed by seawater at 25 °C. Assume that seawater is a 0.53 M solution of NaCl.
Π =
26_0__
The van't Hoff factor for NaCl = 2, the temperature is 298 K, R = 0.0821 L·atm/K·mol

Π = iMRT = (2)(0.53)(0.0821)(298) = 26 atm
atm
2.5-17. Molar Mass from Osmotic Pressure Exercise
Exercise 2.26:
1.00 L of an aqueous solution containing 0.40 g of a peptide has an osmotic pressure of 3.74 torr at 27 °C. What is the molar mass of the peptide?
Π =
4.92e-3_0__

3.74 torr ×
= 4.92e−03 atm
atm
| 1 atm |
| 760 torr |
molar concentration of the peptide =
2.00e-4_0_3_
Use Equation 2.15 and Π = 4.92e-03 atm, R = 0.0821 L·atm/K·mol, T = 300K, and i = 1 (peptides are nonelectrolytes).

M =
=
= 2.00e−04 M
M
| Π |
| iRT |
| 4.92e−03 atm |
| (1)(0.0821 L\pre{·}atm/K\pre{·}mol)(300 K) |
number of moles of peptide in the solution =
2.00e-4_0_3_

n = M × V = (2.0e−04 M)(1.00 L) = 2.00e−04 mol.
The peptide is in a 1.00-L solution.
mol
molar mass of peptide =
2000_0_2_

Mm =
= 2.0e+03 g/mol
g/mol
| 0.40 g peptide |
| 2.00e−04 mol peptide |
2.5-18. Applications of Osmosis
Purification: Solvents can be purified by a process called reverse osmosis. If a pressure that exceeds the osmotic pressure is applied to a solution, solvent can be forced from the solution into the pure solvent. This process has been used to purify seawater in the Middle East. The challenge to purifying seawater lies in finding membranes that can withstand the large pressure (over 26 atm) required. Biology: Cell membranes are semipermeable. When the solution around a cell has the same colligative concentration as within the cell, the cell maintains its size. However, if the cell is placed in water, water passes into the cell and can rupture it. Placing the cell in a solution with a greater colligative molarity causes water to leave the cell. This is why drinking seawater does not quench your thirst. Water transport in plants: Water enters a tree through the membranes in the roots, but it evaporates from the leaves resulting in a substantial concentration difference between the roots and leaves. The large concentration difference can develop osmotic pressures of up to ~20 atm in tall trees.2.6 Colloids
Introduction
Sometimes, rather than dissolving, one material will be suspended as small aggregates in another. Thus, sand will stay suspended in water as long as the water is stirred; but soon after the stirring has stopped, the sand settles to the bottom of the container. Because these mixtures do not meet the rigorous criterion of a solution, they are called dispersions or suspensions.Objectives
-
•Identify common colloidal suspensions.
