Chapter 3 – The First Law of Thermodynamics
Introduction
In this chapter, we discuss the First Law of Thermodynamics (energy cannot be created or destroyed). In our discussion, we will define some important terms and demonstrate some valuable tools that are required to treat the energy flow in a chemical reaction.3.1 Some Definitions and Conventions
Introduction
Determining the magnitude and direction of the energy flow is a common goal of thermodynamics. However, both the sign and magnitude depend upon the exact definition of the problem. In this section, we introduce some terms that will help us in this task.Objectives
-
•Distinguish between a system, its surroundings, and the universe for a thermodynamic process.
3.1-1. Energy Flow
We first define three important terms:-
•thermodynamic system: That portion of the universe under investigation. It can be a volume in space or a carefully defined set of materials. It is the reference point for the direction of energy flow.
-
•thermodynamic surroundings: That portion of the universe that interacts with the system. Energy flows between the system and its surroundings.
-
•thermodynamic universe: A system and its surroundings.
-
•ΔE = energy change of the system
-
•ΔEsur = energy change in the surroundings
-
•ΔEuniv = energy change in the universe
3.1-2. Cash Flow Analogy
We now apply the definitions of system, surroundings, and sign to a cash flow problem where you write a check for $50 to a friend. The first step in "setting up the books" is to define the system, which we will define as your account. In this problem, only your friend's account interacts with (exchanges money with) the system, so it can be thought of as the surroundings. We define ΔB as the change in the balance of your account (the system); thenΔB = −$50
because money transferred out of the system, which caused your balance to decrease by $50. Similarly, ΔBsur = +$50
because money transferred into the surroundings, which increased the balance in your friend's account by $50. Money was conserved in the process because money was neither created nor destroyed, it was simply transferred from the system to the surroundings. Thus, ΔBuniv = ΔB + ΔBsur = –50 + 50 = 0. If both accounts are held by the same bank, then the bank would be the universe for the problem as no money was tranferred into or out of the bank. However, it is important to realize that the value of ΔB depends upon our definitions. Consider the following possibilities:
-
•your account is the system: ΔB = –$50
-
•your friend's account is the system: ΔB = +$50
-
•the bank is the system: ΔB = 0
3.2 Work, Heat, and Energy
Introduction
Heat and work are forms of energy transfer, and they represent the most common way for systems to exchange energy with their surroundings.Objectives
-
•Calculate the heat absorbed by a system given its heat capacity and temperature change.
-
•Distinguish between heat capacity and specific heat.
-
•State the difference between the effects of work done on and work done by a system.
3.2-1. Work
Consider Figure 3.1, in which a larger mass M is attached to a smaller mass m through a pulley. Upon release, the larger mass would drop and its potential energy would decrease, but as it falls, it exerts a force on the other mass causing it to move up. Work, w, is defined as a force through a distance, so the larger mass does work on the smaller one. For this discussion, we assume that 50 J of work is done. By convention, w is defined as the work done on the system. So we would deduce that w = –50 J if the larger mass is the system, but w = +50 J if the smaller mass is the system. The sign of w is given conversationally by using "on" or "by" as follows:-
•w > 0: the work is done on the system
-
•w < 0: the work is done by the system
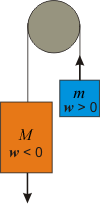
Figure 3.1: Work and the Sign of w
3.2-2. Sign of w Exercise
Exercise 3.1:


A person lifts a 70 kg mass to a height of 2.0 m, which changes the potential energy of the mass by 1.4 kJ.
1.4 kJ of work was done ______________ the person, and 1.4 kJ of work was done ______________ the mass.
-
First answer blank:
-
on The person did the work, so the work was done BY the person.
-
by

-
Second answer blank:
-
on
-
by The energy of the mass increased because work was done ON it by the person.

If the person is the system
w =
-1.4_0__
Work was done BY the person, so the person's energy decreases.
kJ

If the mass is the system
w =
+1.4_0__
Work was done ON the mass, so its energy increases.
kJ

3.2-3. Heat
Heat and work are the most common ways for energy to be transferred between a system and its surroundings.
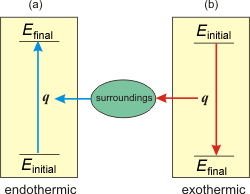
Figure 3.2: Heat and the Sign of q
(a) Endothermic process: q > 0 and heat flows from the surroundings into the system. (b) Exothermic process: q < 0 and heat flows from the system into the surroundings.
3.2-4. Sign of q Exercise
Exercise 3.2:




A piece of metal is placed into hot water and 120 J of heat is transferred from the water to the metal.
If the metal is the system,
q =
+120___
The heat was transferred to the metal, so its energy increases.
J

and the process is said to be ______________.
-
exothermic The heat went INTO the metal.
-
endothermic

If the water is the system,
q =
-120___
The heat was transferred from the water, so its energy decreases.
J

and the process is said to be ______________.
-
exothermic
-
endothermic The heat EXITED the water.

120 J of heat were ______________ by the metal and 120 J of heat were ______________ by the water.
-
First answer blank:
-
absorbed
-
given off The heat went into the metal.

-
Second answer blank:
-
absorbed The heat left the water.
-
given off

3.2-5. Heat Capacity and Specific Heat
The heat capacity of a substance depends upon its mass, but the specific heat does not.
| Substance |
Specific Heat (J·g–1·C–1) |
|---|---|
| Al(s) | 0.90 |
| Cu(s) | 0.38 |
| Fe(s) | 0.44 |
| Hg(l) | 0.14 |
| Kr(g) | 0.25 |
| N2(g) | 1.04 |
| CCl4(g) | 0.86 |
| C2H5OH(l) | 2.46 |
| H2O(l) | 4.18 |
| H2O(s) | 2.00 |
| H2O(g) | 2.00 |
Table 3.1: Specific Heats of Selected Substances
3.2-6. Specific Heat Exercise
Exercise 3.3:
How many kilojoules of heat are required to heat 17 g of ice from –22 °C to –10 °C?
The specific heat of ice is 2.0 J·g–1·°C–1.
The heat capacity of 17 g of ice is
34_0__
Use Equation 3.2 with the given mass and specific heat: 
C = (17 g)(2.0 J · g−1 · °C−1) = 34 J · °C−1
J·°C–1
The temperature change is
ΔT =
12_0__

ΔT = Tfinal − Tinitial = −10 − (−22) = +12 °C
°C
The amount of heat required is
q =
0.41_0__

q = CΔT = (34 J · °C−1)(12 °C) = 4.1e+02 J = 0.41 kJ
kJ
3.2-7. Kinetic and Potential Energy
Energy can be kinetic or potential.
-
•Kinetic energy is energy of motion. Any particle in motion has the capacity to do work and to transfer heat. For example, a moving truck can move another object (do work on it) by colliding with it. It can transfer its energy as heat through the brake drums and tires when the brakes are applied.
-
•Potential energy is energy of position. A stopped truck at the top of a hill has no kinetic energy, but its potential energy can be converted into kinetic energy by releasing the brake. The atoms in molecules have potential energy because of their positions relative to other atoms.
3.3 The First Law of Thermodynamics
Introduction
"Energy cannot be created or destroyed" is one of many statements of the First Law of Thermodynamics. In this section, we discuss how this law impacts the energy of a system.Prerequisites
-
•(CAMS) 9.1 First Law of Thermodynamics
Objectives
-
•Use the expression,ΔE = q + w,to determine how much of an energy flow is in the form of heat and how much is in the form of work.
-
•Define a state function.
-
•Calculate the amount of work associated with a change in the number of moles of gas in a reaction carried out at constant temperature and pressure.
3.3-1. First Law of Thermodynamics
Energy is conserved in all processes.
ΔEuniv = ΔE + ΔEsur = 0,
which leads to the following statement of the first law:
The above shows that, although it cannot be created or destroyed, energy can be transferred between a system and its surroundings. Heat and work are the two most common ways of transferring energy. Thus, the energy of a system is increased when the surroundings transfers heat into the system and/or does work on it. The energy of the system decreases when it transfers heat to the surroundings or does work on them. This relationship is expressed mathematically in the following, which is another statement of the First Law of Thermodynamics:
3.3-2. First Law Exercise
Exercise 3.4:
What energy change is experienced by a system that absorbs 358 J of heat and does 412 J of work?
ΔE =
-54_0__
Absorbing heat increases the energy (q = +358 J), but doing work decreases the energy

(w = −412 J).
ΔE = q + w = 358 + (−412) = −54 J
J
3.3-3. Partitioning Energy Changes
Energy change can be partitioned into heat and work.
(ΔE = q + w)
in the following animation by transferring the energy to the thermal and mechanical surroundings:
-
•The mechanical surroundings is that portion of the surroundings that exchanges energy with the system in the form of work. In the following, the system can lift another block. In doing so, the system does work on the lifted block, so some of the energy change of the system is transferred as work.
-
•The thermal surroundings is that portion of the surroundings that exchanges energy with the system in the form of heat. In the following, the falling system is stopped by friction, which converts the kinetic energy of the system into heat that is transferred to the thermal surroundings.
Energy is Partitioned into Heat and Work ΔE is a state function, so it is path independent, but q and w do depend upon the path.
3.3-4. State Functions
In the experiments described in the previous animation, we examined the transition between the same initial and final states by three different thermodynamic paths that differed in their distributions of q and w. ΔE was the same for each path because ΔE depends only upon the initial and final states—not on how they were achieved:ΔE = Efinal − Einitial.
Properties, like energy, that depend only upon the state of the system are called state functions. The fact that energy is a state function means that ΔE for a chemical process depends only upon the states of the reactants and products, not on the manner in which they react! This is an important property because it allows us to determine ΔE for a reaction using any path—even one that is unreasonable—as long as the reactants and products remain the same. Both q and w are path dependent, so they are not state functions. q and w for a reaction depend not only on the reactants and products; they also depend on how the reaction is carried out.
3.3-5. Changing the Number of Moles of Gas in a Reaction
Δng is the change in the number of moles of gas.
ΔT = 0
and ΔP = 0.
These conditions are very common and they simplify the thermodynamics, so we limit our discussions to processes run at constant temperature and pressure.
Almost all reactions exchange energy with the thermal surroundings, but those involving gases can also exchange energy with the mechanical surroundings, and we now show how to partition the energy change of a reaction involving gases into heat and work. We begin by expressing the ideal gas law for a mixture as the following:
ng is the total number of moles of gas in the mixture, but ng can change during a reaction as gases are consumed or created. Under conditions of constant temperature and pressure, P, R, and T are all constant, so the volume of the container must also change if ng changes. The relationship is expressed as follows:
ΔV is the volume change, and Δng is the change in the total number of moles of gas. The change in the number of moles of gas in a reaction would be determined as follows:
Example:
Δng would be determined from the chemical equation 2 H2(g) + O2(g) → 2 H2O(g) as
Δng = 2 moles gaseous product – 3 moles gaseous reactants = –1 mole gas, but that is
–1 mole of gas for every two moles of H2O that are produced. However, if the reaction actually produced 0.5 mol H2O, then Δng would be determined as follows:
Δng would be determined from the chemical equation 2 H2(g) + O2(g) → 2 H2O(g) as
Δng = 2 moles gaseous product – 3 moles gaseous reactants = –1 mole gas, but that is
–1 mole of gas for every two moles of H2O that are produced. However, if the reaction actually produced 0.5 mol H2O, then Δng would be determined as follows:
Δng = 0.5 mol H2O ×
= −0.25 mol gas
| −1 mol gas |
| 2 mol H2O |
3.3-6. Change in Moles Exercise
Exercise 3.5:
Determine the value of Δng for each of the following processes.
N2(g) + 3 H2(g) → 2 NH3(g)
Δng =
-2_0__
Two moles of produced gas and four moles of reacting gas.
mol

Cl2(g) + H2(g) → 2 HCl(g)
Δng =
0_0__
Two moles of produced gas and two moles of reacting gas.
mol

H2O(l) → H2O(g)
Δng =
1_0__
One mole of produced gas and zero moles of reacting gas. (Don't count solids and liquids!)
mol

NH4Cl(s) → NH3(g) + HCl(g)
Δng =
2_0__
Two moles of produced gas and zero moles of reacting gas. (Solids are not counted.)
mol

3.3-7. Volume Change Example
Work is done whenever gases are produced or consumed in a reaction.
2 NH3(g) → N2(g) + 3 H2(g)
Δng = 4 mol − 2 mol = 2 moles of gas
Each molecule represents one mole of gas, so the vessel starts with 4 mol reactant (NH3) and finishes with 8 mole product (2 mol N2 + 6 mol H2). The increase of 4 mol of gas at constant T and P results in the volume change shown in yellow.
3.3-8. PV Work
The piston moves as the volume changes in the animation above, so work was done when the number of moles of gas changed. We now determine how much work was done. The work done by an object is the force exerted by the object times the distance moved, Fd. However, w is defined as the work done on the object, sow = −Fd.
A force is exerted by the expanding gas because it must push back the atmosphere, which is exerting a pressure on the cylinder. We will call this pressure the opposing pressure, Pop. The force that must be overcome by the expanding gas is then PopA, where A is the cross-sectional area of the piston. Consequently, we can write that w = −PopAd,
but the product of the cross-sectional area of the piston times the distance that it moves is the volume change that the gas undergoes (Ad = ΔV),
so we can express the work done on the gas as
Recall that PΔV = ΔngRT for processes at constant temperature and pressure, so we can also express the work done on the gases in a reaction as
PV Work by an Expanding Gas: Please see the animation in the previous section for a description of the reaction. A is the cross-sectional area of the piston. Pop is the opposing pressure exerted by the atmosphere (usually 1 atm), d is the distance moved by the piston. The distance moved times the cross-sectional area is the volume change, ΔV, shown in yellow.
3.3-9. Expansion Work Exercise
Exercise 3.6:

How much work is done when 12 g of water evaporates at 25 °C?
Δng =
0.67_0__
Δng applies to the amount that reacts, which is 12 g of H2O.

Δng = 12 g H2O ×
= 0.67 mol H2O
mol H2O
| 1 mol H2O |
| 18 g H2O |
RT =
2.48e3_0__

RT = (8.314 J/mol K)(298 K) = 2.48e+03 J/mol
J/mol
w =
-1.7e3_0__

w = −ΔngRT = −(0.67 mol)(2.48e+03 kJ/mol) = −1.7e+03 J
J
Is the work done "on" or "by" the water?
-
on The gas molecules must push the atmosphere back when they are created, so they must do the work. Alternatively,w < 0,so the work is done by the system.
-
by

3.3-10. PV Work Exercise
Exercise 3.7:
What is the energy change of a gas that absorbs 432 J of heat and expands from 0.932 L to 1.684 L against an opposing pressure of 4.46 atm?
First determine the amount of energy exchanged with the thermal surroundings.
q =
432_0__
The gas absorbs 432 J of heat.
J

Next, use Equation 3.9
w = −PopΔV
to determine the amount exchanged with the mechanical surroundings.
ΔV =
0.752_0__
ΔV = Vfinal – Vinitial = 1.684 L – 0.932 L = 0.752 L
L

w = –PΔV =
-3.35_0__
w = –PΔV = –(4.46 atm)(0.752 L) = –3.35 L · atm
L·atm

Use the fact that 1 L·atm = 101.3 J to convert w from L·atm to J.
w =
-340_1_3_

−3.35 L · atm ×
= −340. J
J
| 101.3 J |
| 1 atm |
Use q and w to determine the energy change.
ΔE =
92_0__
ΔE = q + w = 432 J – 340. J = 92 J
J

3.3-11. Work in Combustion Exercise
Exercise 3.8:

How much work is done by the gases when 5.000 g of butane is combusted at 25 °C and 1 atm?
C4H10(g) + 13/2 O2(g) → 4 CO2(g) + 5 H2O(l)
Δng for the reaction shown above =
-3.5_0__
Δng = (4 + 0) – (13/2 + 1) = –3.5 mol gas/mol C4H10
mol

-
This results in work being done ________________ the system.
-
on
-
by Δng < 0, so the volume of the system decreases.

The number of moles of butane that react is
0.08603_0__

5.000 g C4H10 ×
= 0.08603 mol C4H10
mol
| 1 mol C4H10 |
| 58.12 g C4H10 |
Δng for the combustion of 5.000 g of butane =
-0.3011_0__

0.008603 mol C4H10 ×
= −0.3011 mol gas
mol
| −3.5 mol gas |
| 1 mol C4H10 |
w for the combustion of 5.000 g of butane =
746_0__
w = –ΔngRT = –(–0.3011 mol)(8.314 J/mol·K)(298 K) = 746 J
J

3.4 Enthalpy
Introduction
In the last section, we saw that some of the energy change (ΔngRT) of a reaction carried out at constant pressure is in the form of work as escaping gases push back the atmosphere. This portion of the energy is lost and not available to do other work. Thus, it is only the heat that is absorbed or given off by a reaction that is important in processes carried out at constant pressure. Thus, ΔE does not represent the energy that is important in constant pressure processes. In this section, we define a new thermodynamic function that is more appropriate for these processes.Prerequisites
-
•(CAMS) 9.2 Enthalpy
-
•(CAMS) 9.3 Enthalpies of Combustion
Objectives
-
•Define the enthalpy of reaction and distinguish between it and the energy change of a reaction in terms of the heat absorbed at constant pressure or volume.
-
•Calculate the enthalpy of reaction from the energy change of the reaction and vice versa.
3.4-1. ΔH vs. ΔE
ΔH is the heat absorbed at constant pressure, while ΔE is the heat absorbed at constant volume.
3.4-2. Enthalpy-Energy Exercise
Exercise 3.9:
The enthalpy of vaporization of water at 25 °C is 44.0 kJ·mol–1. What is ΔE for the vaporization of a mole of water at 25 °C?
H2O(l, 25 °C) → H2O(g, 25 °C)
ΔH = 44.0 kJ
Δng =
1_0__
1 – 0 = 1
mol

ΔngRT =
2.48_0__

ΔngRT = (1)(8.314)(298) = 2.48e+03 J = 2.48 kJ.
The answer is expressed in kJ because it will be added to ΔH, which is in kJ.
kJ
ΔE =
41.5 _0__

ΔE = ΔH − ΔngRT = 44.0 − 2.5.
kJ
Note that the energy difference between a mole of liquid and a mole of gas is less than the amount of energy that must be supplied to vaporize a mole of liquid because some energy is used by the escaping gases to "push back the atmosphere."
3.4-3. Enthalpy-Energy Exercise
Exercise 3.10:
Determine ΔHcomb for butane given that ΔE = –244.9 kJ for the combustion of 5.000 g of butane at 25 °C.
Method:
1. Write the chemical equation for the combustion reaction.
2. Determine the number of moles of butane that react. (Mm = 58.12 g/mol)
3. Use the given values to determine ΔE for combustion of one mole of butane.
4. Determine Δng for the combustion of one mole of butane.
5. Determine the amount of energy that is in the form of work.
6. Use Equation 3.11
1. Write the chemical equation for the combustion reaction.
C4H10(g) + 13/2 O2(g) → 4 CO2(g) + 5 H2O(l)
n =
0.08603 _0__

5.000 g C4H10 ×
= 0.08603 mol C4H10
mol
| 1 mol C4H10 |
| 58.12 g C4H10 |
ΔEcomb =
-2847_0__
=
= −2847 kJ/mol C4H10
kJ/mol

| ΔE |
| n |
| −244.9 kJ |
| 0.08603 mol C4H10 |
Δng =
-3.5_0__
4 – 6.5 – 1 = –3.5 mol
mol

ΔngRT =
-8.75 ___

ΔngRT = (−3.5 mol)(8.314 J/mol·K)(298 K) = −8.75e+03 J = −8.75 kJ
kJ/mol
ΔE = ΔH − ΔngRT
to determine the heat of combustion.
ΔHcomb =
-2856_0__
ΔH = ΔE + ΔngRT = –2847 kJ/mol + (–8.75 kJ/mol) = –2856 kJ/mol
kJ/mol

3.5 Standard States and Properties of Enthalpy Changes
Introduction
The enthalpy of a reaction depends upon the states of the reactants (solid, liquid, gas, or solution) and upon the amounts of each of the substances. Thus, thermodynamic data are tabulated at reference states and apply to specific chemical equations. In this section, we discuss these reference states and how the enthalpy is dependent upon how the chemical equation is balanced.Objectives
-
•Identify the standard state of a substance.
3.5-1. Standard States
The standard state is defined by a pressure (1 atm), but there is no standard temperature.
-
•The standard state of a pure substance is the most stable state at 1 atm pressure and the specified temperature. Solids and liquids are assumed to be pure unless specified otherwise.
-
•The standard state of a gas is a partial pressure of 1 atm.
-
•The standard state of a solute is a concentration of 1 M.
-
•a solid at –10 °C
-
•a liquid at 25 °C
-
•a gas at 1 atm pressure at 110 °C
3.5-2. Properties of Enthalpy
The enthalpy change also depends upon the amount of reactant that reacts or product that is formed. For example, consider the following reaction: ΔH° = –852 kJ in the above reaction as it is written. This means that 852 kJ are released for each mole of Fe2O3 or every two moles of Al that react or every 2 mol Fe or 1 mole Al2O3 that are produced. Thus, the following factors can be used to determine the amount of heat liberated from the amount of reactant consumed or product formed:| −852 kJ |
| 1 mol Fe2O3 reacting |
| −852 kJ |
| 2 mol Al reacting |
| −852 kJ |
| 1 mol Al2O3 produced |
| −852 kJ |
| 2 mol Fe produced |
-
•If a reaction is multiplied by some number, then the enthalpy change must be multiplied by the same number.
-
•If a reaction is reversed, the sign of its enthalpy change is reversed.
3.5-3. Balanced Chemical Equation and Enthalpy Change Exercise
Exercise 3.11:
The thermochemical equation for the thermite reaction is:
Fe2O3(s) + 2 Al(s) → Al2O3(s) + 2 Fe(s) ΔH° = –852 kJ
What is the standard enthalpy for the reaction of 1.00 mol of Al with an excess of Fe2O3?
ΔH° =
-426_0__
The given ΔH° is for the reaction of 2 mol Al, but ΔH° for the reaction of 1 mol is requested. Al is a reactant in both the given and requested reaction, so there is no sign change. However, the requested reaction involves only half as much reactant.
kJ

What is the standard enthalpy for the reaction of 2.00 mol of Fe with an excess of Al2O3?
ΔH° =
+852 _0__
The given ΔH° is for the production of 2 mol Fe, but ΔH° for the consumption of 2 mol is requested. The amount of Fe is the same in both, so the magnitudes are the same. However, Fe is a reactant in the requested equation but a product in the given, so the sign must be changed.
kJ

3.6 Hess's Law of Heat Summation
Introduction
Enthalpy is a state function, so the enthalpy change of a process is independent of the path used to convert the initial state into the final state. This means that the enthalpy change of a process can be determined by breaking the process into a series of smaller processes whose enthalpy changes are known. The steps we choose don't even have to be realistic; they only have to move the system from the initial to the final state.Objectives
-
•Apply Hess's Law of Heat Summation to determine the enthalpy of reaction.
3.6-1. Hess's Law
We will frequently use the fact that enthalpy is a state function to deduce its value from other known enthalpies with the use of Hess's Law of Heat Summation. Hess's Law of Heat Summation:-
•If a process can be expressed as the sum of several steps, then the enthalpy change of the process is the sum of the enthalpy changes of the steps.
3.6-2. A Heating Curve
Adding heat to a substance results in either a temperature change or a phase change. For example, consider the heating curve for heating water from 25 °C to 150 °C shown in Figure 3.3. Initially, the heat results only in a temperature change until the boiling point is reached. There is no temperature change as heat is added at the boiling point because all of the heat is used to vaporize the liquid. Once all of the liquid is vaporized, additional heat again causes the temperature to rise. The amount of heat required in each step is determined as follows:-
•Temperature change: Combining Equation 3.2C = msand Equation 3.1q = CΔTHeat, Heat Capacity, and Temperature Change, we see that the heat required to raise the temperature of m grams of a substance by ΔT degrees is ΔH = msΔT.
-
•Phase change: Enthalpies of phase change are usually given in kJ·mol–1, so the enthalpy change required to change the phase of n moles is ΔH = nΔHphase change.
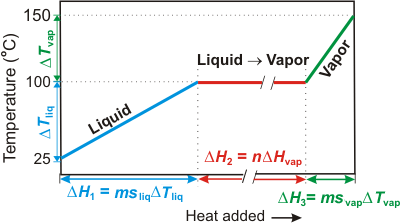
Figure 3.3: Heating Curve for Water from 25 °C to 150 °C
3.6-3. Hess's Law Example
Hess's Law, coupled with the fact that enthalpy change is path independent, allows us to determine enthalpy changes for complicated processes by considering simpler ones. Consider the process of heating water from 25 °C to 150 °C that was discussed above. To determine the heat required for the overall process, we would first break the process down into smaller processes (chemical equations) for which we can readily determine individual enthalpies. The processes are chosen so that they involve only one change, either temperature or phase, but not both.| Process | Chemical Equation |
|---|---|
| Heat the liquid from 25 °C to its boiling point. | H2O(l, 298 K) → H2O(l, 373 K) |
| Vaporize the liquid at its boiling point. | H2O(l, 373 K) → H2O(g, 373 K) |
| Heat the steam to 150 °C. | H2O(g, 373 K) → H2O(g, 423 K) |
Table 3.2
Note that the final state of each process is the same as the initial state of the following process, so these two states cancel when the three processes are added to leave only the initial state of the first process and the final state of the last process (the two states in bold):
Since the process can be represented as the sum of three processes, the enthalpy change for the overall process is the sum of the three enthalpy changes. The enthalpy changes are determined for an expanded problem in the following section.
3.6-4. State Change Exercise
Exercise 3.12:
Use the following table for the thermal properties of water to determine how much heat is required to convert 1.00 mole of ice at –20. °C to steam at 120. °C.
|
Specific Heats (J·g–1·°C) |
|
|---|---|
| solid | 2.0 |
| liquid | 4.18 |
| gas | 2.0 |
| Enthalpies (kJ·mol–1) |
|
| fusion | 6.01 |
| vaporization | 40.7 |
Table 3.3: Some Thermal Properties of Water
First, break the overall process down into a series of smaller processes and determine the value of ΔH for each of the simple processes. Note: the enthalpy units must be the same for each process in order to add them. In this example, we determine the enthalpies in kJ.
| Process | ΔH (kJ/mol) |
|---|---|
| H2O(s, 253 K) → H2O(s, 273 K) |
0.72_0__
This is a temperature change of the solid, so
ΔH = msΔT = (18.0 g)(2.0 J ·g−1·°C)(20. °C) = 720 J = 0.72 kJ.
|
| H2O(s, 273 K) → H2O(l, 273 K) |
6.01_0__
This is a phase change (fusion or melting), so
ΔH = nΔHfus = (1.00 mol)(6.01 kJ·mol−1) = 6.01 kJ.
|
| H2O(l, 273 K) → H2O(l, 373 K) |
7.52_0__
This is a temperature change of the liquid, so
ΔH = msΔT = (18.0 g)(4.18 J·g−1·°C) (100. °C) = 7524 J = 7.52 kJ.
|
| H2O(l, 373 K) → H2O(g, 373 K) |
40.7_0__
This is a phase change (vaporization), so
ΔH = nΔHvap = (1.00 mol)(40.7 kJ·mol−1) = 40.7 kJ.
|
| H2O(g, 373 K) → H2O(g, 393 K) |
0.72_0__
This is a temperature change of the gas, so
ΔH = msΔT = (18.0 g)(2.0 J·g−1·°C)(20. °C) = 720 J = 0.72 kJ.
|
Use the above values and Hess's Law to determine ΔH for the entire process.
| Process | ΔH (kJ/mol) |
|---|---|
| H2O(s, 253 K) → H2O(g, 393 K) |
55.7_0__
ΔH = ΔH1 + ΔH2 + ΔH3 + ΔH4 + ΔH5 = 0.72 + 6.01 + 7.52 + 40.7 + 0.72 = 55.7 kJ
|
3.6-5. Any Path Will Do
Although some ice may sublime, and some of the water vaporizes prior to the boiling point, the processes used in the preceding example follow closely those that actually occur during the heating process. However, enthalpy is a state function, so we are free to choose any path, even one that is totally unrelated to the overall process under consideration. As long as the sum of the processes in the path chosen sum to the overall process, we can use Hess's Law. One path that we can sometimes use is to combust all of the reactants and then let the products of the combustion recombine to produce the desired products. To do this, we use heats of combustion, which are defined as follows:-
•Enthalpy of combustion is the heat absorbed when one mole of a substance reacts with oxygen.
3.6-6. Using Heats of Combustion in the Path
Exercise 3.13:
Given the following combustion reactions:
-
1CH4 + 2 O2 → 2 H2O + CO2 ΔH1 = –890. kJ
-
2C2H6 + 7/2 O2 → 3 H2O + 2 CO2 ΔH2 = –54 kJ
-
3H2 + 1/2 O2 → H2O ΔH3 = –142 kJ
We must rearrange the given chemical equations (multiply each by a number and/or reverse the reaction) so that the sum of the resulting equations produces the desired equation. Reversing the direction of a reaction changes its sign, so use a minus sign with the multiplier to indicate that the reaction must be reversed.
Each reactant and product appears in only one of the given reactions, so we can construct the desired reaction from the individual molecules.
Two molecules of CH4 appear on the reactant side of the desired reaction, and one molecule appears on the reactant side of Equation 1.
The multiplier that should be applied to Equation 1 is
2___
There is 1 CH4 in Equation 1 but there are 2 CH4 in the desired equation, so Equation 1 must be multiplied by 2. CH4 is a reactant in both, so the sign is positive.

The resulting chemical equation is the following. (Denote any subscripts with an underscore. For example, NH_3 for NH3. Place a single space between the coeffient and the compound. Omit any coefficients of 1.)
| Eq A = |
o_2 CH_4_s
Multiplying Equation 1 by 2 yields 2 CH4 + 4 O2 → 4 H2O + 2 CO2
|
+ |
o_4 O_2_s
Multiplying Equation 1 by 2 yields 2 CH4 + 4 O2 → 4 H2O + 2 CO2
|
→ |
o_4 H_2O_s
Multiplying Equation 1 by 2 yields 2 CH4 + 4 O2 → 4 H2O + 2 CO2
|
+ |
o_2 CO_2_s
Multiplying Equation 1 by 2 yields 2 CH4 + 4 O2 → 4 H2O + 2 CO2
|
The enthalpy change is
ΔHA =
-1780_0_3_
If we multiply the chemical equation by 2, we must multiply its enthalpy change by 2.
kJ

One molecule of C2H6 is required on the product side, and one molecule of C2H6 appears on the reactant side of Equation 2.
The multiplier that should be applied to Equation 2 is
-1_0__
There is 1 C2H6 in Equation 2 and 1 C2H6 in the desired equation, so the coefficients of Equation 2 do not need to be changed. However,C2H6 is a reactant in Equation 2, but it is a product in the desired equation, so the sign is negative. Multiply by –1.

The resulting chemical equation is the following. (Denote any subscripts with an underscore. For example, NH_3 for NH3. Place a single space between the coeffient and the compound. Omit any coefficients of 1.)
| Eq B = |
o_3 H_2O_s
Reversing Equation 3 yields 3 H2O + 2 CO2 → C2H6 + 7/2 O2
|
+ |
o_2 CO_2_s
Reversing Equation 3 yields 3 H2O + 2 CO2 → C2H6 + 7/2 O2
|
→ |
o_C_2H_6_s
Reversing Equation 3 yields 3 H2O + 2 CO2 → C2H6 + 7/2 O2
|
+ |
o_7/2 O_2_s
Reversing Equation 3 yields 3 H2O + 2 CO2 → C2H6 + 7/2 O2
|
The enthalpy change is
ΔHB =
54_0__
Reversing the reaction changes the sign of the enthalpy.
kJ

One molecule of H2 appears on the product side of the desired equation, and one molecule appears as a reactant in Equation 3.
The multiplier that should be applied to Equation 3 is
-1_0__
There is 1 H2 in Equation 3 and 1 H2 in the desired equation, so the coeficients of Equation 3 do not need to be changed. However, H2 is a reactant in Equation 2, but it is a product in the desired equation, so the sign is negative. Multiply by –1.

The resulting chemical equation is the following. (Denote any subscripts with an underscore. For example, NH_3 for NH3. Place a single space between the coeffient and the compound. Omit any coefficients of 1.)
| Eq C = |
o_H_2O_s
Reversing Equation 3 yields H2O → H2 + 1/2 O2
|
→ |
o_H_2_s
Reversing Equation 3 yields H2O → H2 + 1/2 O2
|
+ |
o_1/2 O_2_s
Reversing Equation 3 yields H2O → H2 + 1/2 O2
|
The enthalpy change is
ΔHC =
142 _0__
Reversing the reaction changes the sign of the enthalpy.
kJ

The chemical equation produced by the sum of equations A, B, and C is the following. (Denote any subscripts with an underscore. For example, NH_3 for NH3. Place a single space between the coeffient and the compound. Omit any coefficients of 1.)
|
o_2 CH_4_s
The sum produces 4 CO2 and 4 H2O on each side, so they cancel. The result is the desired equation.
|
→ |
o_C_2H_6_s
The sum produces 4 CO2 and 4 H2O on each side, so they cancel. The result is the desired equation.
|
+ |
o_H_2_s
The sum produces 4 CO2 and 4 H2O on each side, so they cancel. The result is the desired equation.
|
The enthalpy change for the above reaction is ΔH =
-1584_0__
Since the desired reaction can be expressed as the sum of the three given reactions, the enthalpy of the reaction is the sum of the enthalpies of the three given reactions: 
ΔH = −1780 + 54 + 142 = −1584 kJ
kJ
3.6-7. Heats of Combustion Summary
We saw in the preceding example that the enthalpy of the reaction2 CH4 → C2H6 + H2
ΔH = 2ΔHcomb(CH4) − ΔHcomb(C2H6) − ΔHcomb(H2)
3.7 Enthalpies (or Heats) of Formation
Introduction
In the previous section, we saw that the enthalpy of a reaction can be determined from the heats of combustion of the reactants and products. This would be an excellent method to use to determine enthalpies of reactions, but it is limited to reactions in which all reactants and products react with oxygen, and not all compounds do. Thus, another, more general, reaction needs to be used. The reaction that is used is the formation reaction; not all compounds combust, but they all form.Objectives
-
•Determine the enthalpy of reaction given the heats of formation of the reactants and products.
-
•Determine the enthalpy of formation of one of the reactants or products of a reaction given the ΔH of the reaction and the heats of formation of all other participants in the reaction.
3.7-1. Definition
The standard heat of formation,ΔHf°,
of a compound is the heat absorbed when one mole of the compound is formed from its elements in their standard states. For example, saying that "the heat of formation of hydrogen chloride is –92.3 kJ/mol" implies the following thermochemical equation.
1/2 H2(g) + 1/2 Cl2(g) → HCl(g) ΔH° = –92.3 kJ
O2(g) → O2(g) ΔH° = 0
3.7-2. Writing Formation Reaction Exercise
Exercise 3.14:
Write the formation reaction for each of the following. Order the elements in the same order they appear in the given compound. Denote any subscripts with an underscore. For example, NH_3 for NH3. Place a single space between the coeffient and the compound. Omit any coefficients of 1. Be sure to indicate the state of each substance as (s), (l), or (g) and express non-integer coefficients as fractions.
C12H22O11(s)
|
o_12 C(s)_s
The standard state of carbon is solid graphite. Hydrogen and oxygen are diatomic gases. The coefficient of C12H22O11 must be 1, and C12H22O11 must be the only product.
|
+ |
o_11 H_2(g)_s
The standard state of carbon is solid graphite. Hydrogen and oxygen are diatomic gases. The coefficient of C12H22O11 must be 1, and C12H22O11 must be the only product.
|
+ |
o_11/2 O_2(g)_s
The standard state of carbon is solid graphite. Hydrogen and oxygen are diatomic gases. The coefficient of C12H22O11 must be 1, and C12H22O11 must be the only product.
|
→ |
o_C_12H_22O_11(s)_s
The standard state of carbon is solid graphite. Hydrogen and oxygen are diatomic gases. The coefficient of C12H22O11 must be 1, and C12H22O11 must be the only product.
|
Na2O(s)
|
o_2 Na(s)_s
Sodium is a solid and oxygen in a diatomic gas. Na2O is the only product and its coefficient must be 1.
|
+ |
o_1/2 O_2(g)_s
Sodium is a solid and oxygen in a diatomic gas. Na2O is the only product and its coefficient must be 1.
|
→ |
o_Na_2O(s)_s
Sodium is a solid and oxygen in a diatomic gas. Na2O is the only product and its coefficient must be 1.
|
NH3(g)
|
o_1/2 N_2(g)_s
Nitrogen and hydrogen are diatomic gases. NH3 is the only product and its coefficient must be one.
|
+ |
o_3/2 H_2(g)_s
Nitrogen and hydrogen are diatomic gases. NH3 is the only product and its coefficient must be one.
|
→ |
o_NH_3(g)_s
Nitrogen and hydrogen are diatomic gases. NH3 is the only product and its coefficient must be one.
|
(NH4)2Cr2O7(s)
|
o_N_2(g)_s
Chromium is a solid. Nitrogen, hydrogen, and oxygen are diatomic gases.
|
+ |
o_4 H_2(g)_s
Chromium is a solid. Nitrogen, hydrogen, and oxygen are diatomic gases.
|
+ |
o_2 Cr(s)_s
Chromium is a solid. Nitrogen, hydrogen, and oxygen are diatomic gases.
|
+ |
o_7/2 O_2(g)_s
Chromium is a solid. Nitrogen, hydrogen, and oxygen are diatomic gases.
|
→ |
o_(NH_4)_2Cr_2O_7(s)_s
Chromium is a solid. Nitrogen, hydrogen, and oxygen are diatomic gases.
|
3.7-3. Using Heats of Formation
The path that is assumed when heats of formation are used involves breaking up the reactant molecules into their elements, then combining the elements that were produced to form the products. The application of Hess's Law to the process can be summarized as follows:-
•The enthalpy of any reaction can be determined as the sum of the enthalpies of formation of the products, each multiplied by its coefficient in the balanced equation, minus the sum of the enthalpies of formation of the reactants, each multiplied by its coefficient in the balanced equation.
-
•(ΔH°f)Pis the standard heat of formation of the product whose coefficient in the balanced equation is cP.
-
•(ΔH°f)Ris the standard heat of formation of the reactant whose coefficient in the balanced equation is cR.
ΔH° = 2ΔH°f(Al) + 3ΔH°f(CO2) − ΔH°f(Al2O3) − 3ΔH°f(CO)
ΔH° = 2(0) + 3(–393.51) – (–1676) – 3(–110.52) = 827 kJ
3.7-4. Heat of Combustion from Heats of Formation Exercise
Exercise 3.15:
Determine the standard heat of combustion of ethanol, C2H5OH(l), at 298 K.
First, write the combustion reaction for C2H5OH(l). The carbon and hydrogen atoms are oxidized to carbon dioxide and water, respectively. At 298 K, the water is a liquid. Denote any subscripts with an underscore. For example, NH_3 for NH3. Place a single space between the coeffient and the compound. Omit any coefficients of 1. When writing the reaction, be sure to include the states of matter and express noninteger coefficients as fractions.
|
o_C_2H_5OH(l)_s
The reaction is: C2H5OH(l) + 3 O2(g) yields 2 CO2(g) + 3 H2O(l).
|
+ |
o_3 O_2(g)_s
The reaction is: C2H5OH(l) + 3 O2(g) yields 2 CO2(g) + 3 H2O(l).
|
→ |
o_2 CO_2(g)_s
The reaction is: C2H5OH(l) + 3 O2(g) yields 2 CO2(g) + 3 H2O(l).
|
+ |
o_3 H_2O(l)_s
The reaction is: C2H5OH(l) + 3 O2(g) yields 2 CO2(g) + 3 H2O(l).
|
Next, use the resource titled Thermodynamic Properties to determine the heat of formation of each product and reactant.
C2H5OH(l)
-277.7_0__
Be sure you get the heat of formation for the liquid.
kJ/mol

O2(g)
0_0__
Oxygen is an element in its standard state.
kJ/mol

CO2(g)
-393.51_0__
Check the table of Heats of Formation in the Resources.
kJ/mol

H2O(l)
-285.83_0__
Be sure you get the heat of formation for the liquid.
kJ/mol

Finally, use Equation 3.12
ΔH° =
−
to determine the enthalpy of combustion of ethanol.
| cP(ΔH°f)P | |
 | |
| cR(ΔH°f)R | |
 | |
ΔHcomb =
-1366.8_0__

ΔH = 2(−393.51) + 3(−285.83) − 1(−277.7) − 3(0)
kJ/mol
3.7-5. Heats of Formation from Heat of Combustion Exercise
Heats of formation are not always determined from direct measurement. For example, when C(s) and H2(g) react, a number of different compounds will be produced. Consequently, the heat of formation of something like C6H6 cannot be determined directly. Instead, the heat of reaction for a different reaction is measured and used with known heats of formation to determine the unknown heat of formation. The heat of formation of octane is determined from its heat of combustion in the following example.3.7-6. Exercise
Exercise 3.16:
The enthalpy of combustion of octane (C8H18 is –5494 kJ/mol). What is the heat of formation of octane?
First, write the combustion reaction for C8H18(l). The carbon and hydrogen atoms are all oxidized to carbon dioxide and water. At 298 K, the water is a liquid. Denote any subscripts with an underscore. For example, NH_3 for NH3. Place a single space between the coeffient and the compound. Omit any coefficients of 1. Express all noninteger coefficients as fractions and include the states of matter.
|
o_C_8H_18(l)_s
The reaction is: C8H18(l) + 25/2 O2(g) → 8 CO2(g) + 9 H2O(l)
|
+ |
o_25/2 O_2(g)_s
The reaction is: C8H18(l) + 25/2 O2(g) → 8 CO2(g) + 9 H2O(l)
|
→ |
o_8 CO_2(g)_s
The reaction is: C8H18(l) + 25/2 O2(g) → 8 CO2(g) + 9 H2O(l)
|
+ |
o_9 H_2O(l)_s
The reaction is: C8H18(l) + 25/2 O2(g) → 8 CO2(g) + 9 H2O(l)
|
Next, use the resource titled Thermodynamic Properties to determine the heat of formation of each of the other compounds in the reaction.
O2(g)
0___
Oxygen is an element in its standard state.
kJ/mol

CO2(g)
-393.51_0__
Check the table of Heats of Formation in the Resources.
kJ/mol

H2O(l)
-285.83_0__
Be sure you get the heat of formation for the liquid.
kJ/mol

Write the expression for the heat of combustion in terms of the heats of formation and solve it for the heat of formation of octane.
ΔHf =
-227_0__
kJ/mol

| ΔHcomb | = | 8ΔHf(CO2) + 9 ΔHf(H2O) −25/2ΔHf(O2) − ΔHf(C8H18) |
| −5494 | = | 8(−393.5) + 9(−285.8) − 25/2(0) − ΔHf(C8H18) |
| ΔHf(C8H18) | = | 5494 − 8(393.5) − 9(285.8) = −227 kJ/mol |
3.8 Bond Dissociation Energies
Introduction
Although tables of heats of formation are extensive, there are still many compounds whose heats of formation are unknown. However, all chemical reactions involve breaking and forming bonds and the enthalpy of a reaction can be approximated from the energies of the broken and formed bonds. In this section, we define the bond or dissociation energy, show how bond energies can be determined from heats of formation, and finally show how bond energies can be used to approximate the enthalpy of any reaction.Prerequisites
-
•(CAMS) 9.4 Bond Energies
Objectives
-
•Determine the enthalpy of atomization of a molecule and the average bond energy of its bonds when all of the bonds are between the same pair of atoms.
-
•Use bond energies to estimate enthalpies of gas-phase reactions.
3.8-1. Definition
The bond energy or dissociation energy, D, is the energy required to break a mole of bonds in the gas phase. When all of the bonds in a gas phase molecule are broken to produce the constituent atoms in the gas phase, the molecule is said to be atomized and the energy required to atomize a mole of molecules is called the atomization energy, ΔHatom. Note that the atoms, not the elements in their standard states, are the products of atomization. The chemical equation for the atomization of CH4 is CH4(g) → C(g) + 4 H(g)
ΔHatom = ΔHf(C) + 4ΔHf(H) − ΔHf(CH4) = 4DC-H
3.8-2. Determining a Bond Energy Exercise
Exercise 3.17:
What is the average N–O bond energy in NO2?
Our strategy is to determine the atomization energy from heats of formation and then relate that to the N–O bond energy.
Write the atomization reaction for NO2. (Denote any subscripts with an underscore. For example, NH_3 for NH3. Place a single space between the coeffient and the compound. Omit any coefficients of 1. Include states of matter.)
|
o_NO_2(g)_s
The reaction is: NO2(g) → N(g) + 2 O(g).
|
→ |
o_N(g)_s
The reaction is: NO2(g) → N(g) + 2 O(g).
|
+ |
o_2 O(g)_s
The reaction is: NO2(g) → N(g) + 2 O(g).
|
NO2
34_0__
The value listed in the tables is 34 kJ/mol.
kJ/mol

N
473_0__
The value listed in the tables is 473 kJ/mol.
kJ/mol

O
249_0__
The value listed in the tables is 249 kJ/mol.
kJ/mol

Use the heats of formation to determine the atomization energy of NO2.
ΔHatom =
937 _0__
ΔH = products – reactants = 473 + 2(249) – 34 = 937 kJ
kJ/mol

Determine the average bond strength given that two N–O bonds must be broken to atomize the molecule.
DN–O =
469_0__
2DN–O = 937 kJ, so DN–O = 937/2 = 469 kJ.
kJ/mol

3.8-3. Determining a Bond Energy Exercise
Exercise 3.18:
Determine the average C–F bond energy in CHF3 from the following data.
-
•Enthalpies of formation: C = 717; F = 79; H = 218; CHF3 = –695 kJ/mol
-
•C–H bond energy = 413 kJ/mol
Write the atomization reaction for CHF3. (Denote any subscripts with an underscore. For example, NH_3 for NH3. Place a single space between the coeffient and the compound. Omit any coefficients of 1. Include states of matter.)
|
o_CHF_3(g)_s
The reaction is: CHF3(g) → C(g) + H(g) + 3 F(g).
|
→ |
o_C(g)_s
The reaction is: CHF3(g) → C(g) + H(g) + 3 F(g).
|
+ |
o_H(g)_s
The reaction is: CHF3(g) → C(g) + H(g) + 3 F(g).
|
+ |
o_3 F(g)_s
The reaction is: CHF3(g) → C(g) + H(g) + 3 F(g).
|
Determine the atomization energy of CHF3.
ΔHatom =
1867_0__

ΔHatom = ΔHf(C) + 3ΔHf(F) + ΔHf(H) − ΔHf(CHF3) = 717 + 218 + 3(79) − (−695) = 1867
kJ/mol
Use the given bond energy to determine the energy of three C–F bonds.
3DC–F =
1454_0__

ΔHatom = DC–H + 3DC–F
3DC–F = ΔHatom − DC–H = 1867 − 413 = 1454
Determine the average C–F bond energy in CHF3.
DC–F =
484_0__
DC–F = 3DC–F/3 = 1454/3 = 484
kJ/mol

3.8-4. Enthalpies of Reaction from Bond Energies
Reactions involve breaking and forming bonds, so enthalpies of reaction can be estimated with bond energies. The path assumed for a reaction when bond energies are used involves breaking all of the relevant reactant bonds to produce fragments and then combining the fragments so as to produce the desired products. Application of Hess's Law to the process can again be summarized in a simple fashion.-
•The enthalpy of a reaction can be estimated as the energy required to break the reactant bonds minus the energy released when the product bonds are formed.
3.8-5. Bond Energy Table
Bond energies are a convenient way to estimate reaction enthalpies, and a table of bond energies of common bonds can be found in the resource titled Bond Energies. For completeness, it is also given below.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Table 3.4: Common Bond Energies (kJ·mol–1)
3.8-6. Using Bond Energies Exercise
Exercise 3.19:
Use bond energies to estimate the heat of formation of NH3.
1) Write the chemical equation (no states needed) for the formation reaction. (Express all noninteger coefficients as fractions.)
|
o_1/2_s
The formation reaction is the reaction in which ONE mole of a substance is produced from its elements in their standard states.
N2
|
+ |
o_3/2_s
The formation reaction is the reaction in which ONE mole of a substance is produced from its elements in their standard states.
H2
|
→ |
1_0__
The formation reaction is the reaction in which ONE mole of a substance is produced from its elements in their standard states.
NH3
|
2) Draw Lewis structures for each compound to identify multiple bonds.
Energy Reactant Bonds
1125___
The NN bond is a triple bond, so
3/2DHH + 1/2DNN = 3/2(436) + 1/2(941) = 1125 kJ/mol
kJ/mol

Energy Required to Break Reactant Bonds
1173_0__
Three N–H bonds are formed: 3(391) = 1173 kJ/mol
kJ/mol

Use the results of 3 and 4 to determine the enthalpy of formation.
ΔHf =
-48_0__
The enthalpy change is the difference of the energies of the formed – produced bonds = 1125 – 1173 = –48 kJ/mol. The actual heat of formation is –46 kJ/mol, so the estimate is off by less than 5%.
kJ/mol

3.8-7. Using Bond Energies in Reactions that Involve a Simple Solid or Liquid
Bond energies should be applied directly only when all substances in a reaction are gases. However, they can be combined with other thermodynamic quantities to produce valid results for reactions that involve a simple solid or liquid. This is done by applying Hess's Law of Heat Summation to the enthalpy of reaction determined with bond energies and the energy required to convert the solid or liquid into a gas. Consider the example where the heat of combustion of butane at 298 K is determined from bond energies.Example:
Bond energies apply only to molecules in the gas phase, so using bond energies alone we would obtain the enthalpy of the following reaction.
Using a table of bond energies (Bond Energies), we can determine the enthalpy of Reaction 1 as follows.
However, water is a liquid at 298 K, not a gas, so the heat of vaporization of water must be combined with Reaction 1 to convert the gas to a liquid. Five moles of H2O are produced, so we use the following:
Adding Reactions 1 and 2 provides the chemical equation for the combustion as the 5 H2O(g) cancels in the addition. Adding their enthalpy changes provides the heat of combustion.
Bond energies apply only to molecules in the gas phase, so using bond energies alone we would obtain the enthalpy of the following reaction.
( 1 )
C4H10(g) + 13/2 O2(g) → 4 CO2(g) + 5 H2O(g)
| ΔH | = | 3DC−C + 10DC−H + 6.5DO=O − 8DC=O − 10DO−H |
| = | 3(347) + 10(413) + 6.5(495) − 8(799) − 10(463) | |
| = | −2634 kJ |
( 2 )
5 H2O(g) → 5 H2O(l) ΔH = −5ΔHvap = −5(44.0) = −220. kJ
| C4H10(g) + 13/2 O2(g) → 4 CO2(g) + 5 H2O(l) ΔHcomb | = | −2634 − 220. |
| = | −2854 kJ |
3.8-8. Using Bond Energies for a Reaction with a Solid Exercise
Exercise 3.20:
Use bond energies to estimate the heat of formation of ethene (C2H4).
Write the balanced chemical equation for the formation as determined solely from bond energies. (Denote any subscripts with an underscore. For example, NH_3 for NH3. Place a single space between the coeffient and the compound. Omit any coefficients of 1. Include states of matter.)
|
Reaction 1:
o_2 C(g)_s
All substances must be gases, so 2 C(g) + 2 H2(g) → C2H4(g)
|
+ |
o_2 H_2(g)_s
All substances must be gases, so 2 C(g) + 2 H2(g) → C2H4(g)
|
→ |
o_C_2H_4(g)_s
All substances must be gases, so 2 C(g) + 2 H2(g) → C2H4(g)
|
Draw Lewis structures and use bond energies to determine the enthalpy for Reaction 1:
ΔH1 =
-1392_0__
The carbon-carbon bond in ethene is a double bond, so

ΔH1 = 2D(H–H) − D(C=C) − 4D(C–H) = 2(436) − 612 − 4(413) = −1392 kJ
kJ
The standard state of carbon is graphite. What equation must be added to the above to convert C(g) to C(s)? (Denote any subscripts with an underscore. For example, NH_3 for NH3. Place a single space between the coeffient and the compound. Omit any coefficients of 1. Include states of matter.)
|
Reaction 2:
o_2 C(s)_s
Two moles of carbon gas on the left must be converted to two moles of carbon solid, so the reaction 2 C(s) → 2 C(g).
|
→ |
o_2 C(g)_s
Two moles of carbon gas on the left must be converted to two moles of carbon solid, so the reaction 2 C(s) → 2 C(g).
|
What is the enthalpy of Reaction 2?
ΔH2 =
1433 _0__
Carbon gas is formed from its standard state, so ΔH2 = 2ΔHf = 2(716.7) = 1433 kJ.
kJ

The enthalpy of formation of ethene is:
ΔHf =
41_0__
ΔHf = ΔH1 + ΔH2 = –1392 + 1433 = 41 kJ
kJ

3.9 Calorimetry
Introduction
Heats of formation, heats of combustion, and bond energies are all available in tables and can be used to determine or approximate the enthalpy change of other reactions. However, these tabulated numbers are based on experimental values. In this section, we discuss how those values are obtained. Measuring the amount of heat absorbed or liberated in a process is called calorimetry.Objectives
-
•Calculate the heat of a reaction from the temperature change it causes in a calorimeter with known heat capacity, and decide whether the heat is an enthalpy change or a change in the energy of the system.
3.9-1. A Calorimeter
Calorimetry is the measurement of the heat flow of a process, and a schematic of a simple calorimeter is shown in Figure 3.4. The calorimeter consists of a thermally insulated container, a thermometer, and a carefully measured amount of water. The thermal insulation can range from styrofoam as found in insulated cups to evacuated jackets as found in Thermos bottles. A heat source or sink, which is often a reaction, is then placed in the calorimeter, and the temperature change of the calorimeter is measured.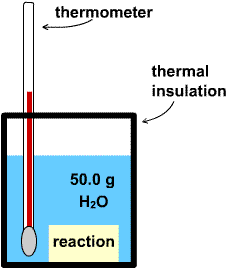
Figure 3.4
The amount of heat that is released or absorbed in a reaction is determined experimentally in a calorimeter. The reaction is usually carried out in a container that is submerged in the water, so the heat flow is determined by measuring the temperature change in the water.
3.9-2. The Calorimetry Equations
Since the water and the reaction are in a thermally insulated container, no heat can enter or leave the system; i.e., qrxn + qcal = 0, which can be rearranged to the following: The heat of the reaction causes only a temperature change in the calorimeter, so we can express qcal as Substituting this expression into Calorimetry Equation 1, we obtain Almost all of the heat that is absorbed by the calorimeter is absorbed by the water, so we can make the following approximation: Substitution of the above into Calorimetry Equation 2 yields a commonly used approximation that relates the heat of reaction to the mass and temperature change of the water in the calorimeter.3.9-3. Using a Calorimeter Exercise
Exercise 3.21:

swater = 4.18 J·g–1°C–1
When the reaction in the simulation below is the reaction of 0.0225 mol X, the temperature of the 50.0 g of water rises from 22.5 °C to 26.4 °C and there is no volume change.
-
The reaction is _______________.
-
exothermic
-
endothermic The temperature of the water rises, so heat must flow into the water from the reaction.

ΔTwater =
3.9_0__
ΔT = tfinal – tinitial = 26.4 – 22.5 = 3.9
°C

swater = 4.18 J·g–1°C–1
qcal =
815_0__
Carry an extra significant figure to reduce rounding errors. J
qcal = msΔT = (50.0 g)(4.18 J·g−1·°C−1)(3.9 °C) = 815 J
Carry an extra significant figure to reduce rounding errors. J
qrxn =
-815_0__
qrxn = –qcal = –815 J
J

ΔH =
-36_0__
Only two sig figs because ΔT is good to only two. kJ/mol
ΔH = qrxn/n = −0.815 kJ/0.0225 mol = −36 kJ/mol
Only two sig figs because ΔT is good to only two. kJ/mol
3.9-4. Determining Specific Heat Exercise
Exercise 3.22:
9.0 g of Al at 100.0 °C are placed in 20.0 mL of water at 20.0 °C contained in a Styrofoam cup. At thermal equilibrium, the temperature of the water and aluminum is 27.1 °C. What is the specific heat of aluminum?
The heat absorbed by the water: swater = 4.18 J·g–1·°C–1
mwater =
20.0_0__
The density of water is 1.0 g/mL, which can be used with the volume to get the mass.
g

ΔTwater =
7.1_0__
ΔT = tfinal – tinitial = 27.1 – 20.0 = 7.1
°C

qwater =
594_0__
qwater = msΔT = (20 g)(4.18 J/g·°C)(7.1 °C) = 594 J
J

The specific heat of Al:
qAl =
-594_0__

qAl = −qwater = −594 J
J
mAl =
9.0_0_2_
The mass of aluminum is given in the question.
g

ΔTAl =
-72.9_0__

ΔT = tfinal − tinitial = 27.1 − 100.0 = −72.9
°C
sAl =
0.91 _0__

sAl =
=
= 0.91 J/g · °C
J·g–1 ·°C–1
| qAl |
| mAlΔTAl |
| −594 J |
| (9.0 g)(−72.9 °C) |
3.9-5. Energy or Enthalpy
The heat of reaction determined in a bomb calorimeter is ΔE, but the heat determined in an open calorimeter is ΔH.
-
•No gases are involved in the reaction or the number of moles of gas does not change. Under these conditions, no PΔV work can be done. This is the case in most reactions that occur in solution.
-
•qrxn = ΔE = ΔH
-
-
•The number of moles of gas does change. Under these conditions, some PΔV work can be done.
-
•at constant pressure: qrxn = ΔH because PΔV work can be done. Any reaction open to the atmosphere or carried out in a piston/cylinder is carried out at constant pressure.
-
•at constant volume: qrxn = ΔE because no PΔV work can be done. This is the case in a bomb calorimeter, where the reaction is carried out in a steel vessel with a cap that is screwed on so no volume change (no work) can take place.
-
3.9-6. Bomb Calorimeter Exercise
Exercise 3.23:

What temperature rise would occur in a bomb calorimeter with a heat capacity of 4.877 kJ/°C when 0.00750 mol C4H10 is burned at 25 °C?
First, decide which thermodynamic property should be used to determine qrxn.
-
ΔHcomb = –2856 kJ/mol The reaction is carried out in a bomb calorimeter, so it is carried out at constant volume. Therefore,qrxn = ΔE.
-
ΔEcomb = –2847 kJ/mol

Next, determine qrxn for the combustion of 0.00750 mol C4H10.
qrxn =
-21.3_0__
qrxn = nΔE = (0.00750 mol)(–2847 kJ/mol) = –21.3 kJ
kJ

ΔT =
4.37_0__

qrxn = −CcalΔTcal, so ΔTcal = −
= −
= 4.37 °C
°C
| qrxn |
| C |
| −21.3 kJ |
| 4.877 kJ/°C |
3.9-7. Heat of Formation from Calorimetry Exercise
Exercise 3.24:
Combustion of 1.00 g of sucrose (C12H22O11) causes the temperature in a bomb calorimeter with a heat capacity of 4.90 kJ/°C to rise from 24.92 to 28.33 °C. What is the standard heat of formation of sucrose? The heats of formation of CO2(g) and H2O(l) are –393.5 kJ/mol and –285.8 kJ/mol, respectively.
heat of reaction in calorimeter
qrxn =
-16.7_0__

ΔTcal = 28.33 − 24.92 = 3.41 °C
qrxn = −CcalΔTcal = −(4.90 kJ/°C)(3.41 °C) = −16.7 kJ
kJ
moles of sucrose reacting
n =
0.00292_0__

1.00 g ×
= 0.00292 mol
mol C12H22O11
| 1 mol |
| 342 g |
energy change for combustion (reaction is carried out in a bomb)
ΔEcomb =
-5.71e3_0_3_
The reaction is carried out in a bomb, so nqrxn = ΔEcomb

ΔEcomb =
=
= −5.71e3 kJ/mol
kJ/mol
| qrxn |
| n |
| −16.7 kJ |
| 0.00292 mol |
change in number of moles of gas in balanced equation
Δng =
0_0__
12 moles of gaseous product and 12 moles of gaseous reactant
mol

heat of combustion of sucrose
ΔHcomb =
-5.71e3_0_3_
Δng = 0, so ΔH = ΔE
kJ/mol

heat of formation of sucrose
ΔHcomb =
-2.16e3_0_3_

ΔHcomb = 12ΔHf(CO2) + 11ΔHf(H2O) − ΔHf(C12H22O11),
so
Hf(C12H22O11) = −ΔHcomb + 12ΔHf(CO2) + 11ΔHf(H2O) = 5.71e+03 + 12(−393.5) + 11(−285.8) = −2.16e+03 kJ/mol
kJ/mol
3.10 Combustion: Food as Fuel
Introduction
The energy that is derived from the metabolism of carbohydrates and fats is essentially the same as is produced by their combustion in a calorimeter. Thus, the calorie content used in nutrition is the same as that derived from calorimetry.3.10-1. Nutrition Labels
In the last example of the previous section, we showed that the heat of combustion of 1 g of C12H22O11, a carbohydrate, is 17 kJ. Indeed, the heat of combustion of most carbohydrates is 17 kJ/g. The heats of combustion of proteins are also 17 kJ/g, while those of fats are 38 kJ/g. These are approximately the same values derived from their metabolism in the body. A dietary calorie (Cal, upper case "C") is actually a kcal of energy and 1 kcal = 4.18 kJ. We can summarize the heats of combustion as follows:| Substance | ΔHcomb (kJ/g) | ΔHcomb (Cal/g) |
|---|---|---|
| carbohydrates | 17 | 4 |
| proteins | 17 | 4 |
| fats | 38 | 9 |
Table 3.5
3.10-2. Nutrition Label Exercise
Exercise 3.25:
Use the heats of combustion given above to determine the number of calories derived from each substance and the total number of calories in one serving of a can of soup with the following nutrition information on one serving.
-
•Total Fat 1 g
-
•Total Carbohydrates 31 g
-
•Total Protein 7 g
Calories from Fat
9 _0__
(1 g)(9 Cal/g)
Cal

Calories from Carbohydrates
124_0__
(31 g)(4 Cal/g)
Cal

Calories from Protein
28_0__
(7 g)(4 Cal/g)
Cal

Total Calories
161_0__
9 + 124 + 28
Cal

