Chapter 6 – Acids and Bases
Introduction
Brønsted acid-base reactions are proton transfer reactions. Acids donate protons to bases. In the process, the acid is converted into its conjugate base and the base into its conjugate acid. A conjugate acid-base pair differ by one and only one proton. The relative strength of an acid is given by its acid dissociation constant, Ka, which is the equilibrium constant for the reaction of the acid with the weak base water. In this chapter, we show how to use the Ka expression to determine equilibrium concentrations in solutions of acids and bases.6.1 Autoionization of Water
Introduction
All of the acid-base reactions we will discuss occur in water, so it is important to understand the acid-base properties of water. Water is said to be amphiprotic because it can behave as either an acid or a base. In fact, the acidity of an aqueous solution is the extent to which water reacts with an acid to produce its conjugate acid H3O1+, the hydronium ion. Similarly, the basicity of a solution is the extent to which water reacts with a base to produce its conjugate base, OH1–. In this section, we examine the relationship between the hydronium and hydroxide ion concentrations in aqueous solutions.Objectives
-
•Convert between [H3O1+] and [OH1–] in an aqueous solution.
6.1-1. Review of Acids and Bases
The following is a brief review of the more thorough treatment of acid-base chemistry which can be found in CAMS Chapter 12. You should refer to that chapter for a more in-depth discussion. The material in this and the following chapter assumes a knowledge of how to write chemical equations for acid-base reactions, so viewing the video in CAMS Section 12.8-1. would be especially helpful. A Lewis base is a substance that contains a lone pair that can be used in a coordinate covalent bond, and a Lewis acid is a substance that has an empty orbital that can be used to share the lone pair in the bond. A Lewis acid-base reaction is the formation of the bond between the acid and the base. The Lewis acid-base reaction between ammonia and acetic acid is represented in Figure 6.1a. In it, the lone pair on ammonia is used to form a covalent bond to a hydrogen atom on the acetic acid. Ammonia contains the lone pair, so it is the base, and acetic acid accepts the lone pair, so it is the acid. In the reverse reaction a lone pair on the acetate ion attacks a proton of the ammonium ion in another Lewis acid-base reaction. This very broad classification allows us to treat many reactions as acid-base reactions. However, the reaction in the figure can also be viewed has a proton transfer from the acid to the base. Although proton transfer reactions can be viewed as Lewis acid-base reactions, a different acid-base theory was developed for this very important branch of chemistry. In Brønsted-Lowery or simply Brønsted theory, an acid is a proton donor and a base is a proton acceptor. Acetic acid has a proton that it can transfer, so it is an acid, while ammonia can accept a proton, so it is a base. The loss of a proton converts the acid into its conjugate base, and the gain of the proton converts the base into its conjugate acid. An acid and a base differ by one proton only and are said to be a conjugate acid-base pair. The only reactants and products present in a Brønsted acid-base reaction are an acid, a base, and their conjugate base and acid. The brackets in Figure 6.1b identify the conjugate acid-base pairs in the reaction of acetic acid and ammonia.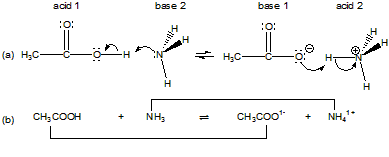
Figure 6.1: Acid-Base Reaction Between Acetic Acid and Ammonia
(a) Lewis formalism (b) Brønsted formalism. The brackets connect conjugate acid-base pairs in the Brønsted formalism.
6.1-2. Ion Product Constant
Kw must be satisfied in all aqueous solutions.
H2O(l) + H2O(l) ⇌ H3O1+(aq) + OH1−(aq)
6.1-3. Acidity and Basicity
If water is the only source of H3O1+ and OH1– ions, then their concentrations must be equal because they are produced in a 1:1 ratio. However, addition of an acid to an aqueous solution increases [H3O1+] and decreases [OH1–] so that the resulting concentrations obey Equation 6.1. Addition of a base has the opposite effect of increasing [OH1–] and decreasing [H3O1+]. Consequently, aqueous solutions can be classified as one of the following types.-
•Neutral Solution: [H3O1+] = [OH1–]
-
•Acidic Solutions: [H3O1+] > [OH1–]
-
•Basic Solutions: [H3O1+] < [OH1–]
6.1-4. Exercise
Exercise: 6.1
What are the hydronium and hydroxide ion concentrations in pure water at 25 °C?
[H3O1+] = [OH1–] =
1.0e-7_0_2_
Let [H3O1+] = [OH1–] = x. Substitute x into Equation 6.1.
[H3O1+][OH1–] = (x)(x) = x2 = 1.0e–14
Solve for x.
x = (1.0e–14)1/2 = 1.0e–7 M. M
[H3O1+][OH1–] = (x)(x) = x2 = 1.0e–14
Solve for x.
x = (1.0e–14)1/2 = 1.0e–7 M. M
HCl is added to water until [H3O1+] = 0.042 M. What is the concentration of the hydroxide ion in the resulting solution at 25 °C?
[OH1–] =
2.4e-13_0__

[OH1−] =
=
= 2.4e−13 M
M
| Kw |
| [H3O1+] |
| 1.0e−14 |
| 0.042 |
What is [H3O1+] in a solution that is 0.50 M in hydroxide ion?
[H3O1+] =
2.0e-14_0_2_

[H3O1+] =
=
= 2.0e−14 M
M
| Kw |
| [OH1−] |
| 1.0e−14 |
| 0.050 |
6.2 The p-Scale
Introduction
Many of the numbers used in this chapter are very small, so they are often expressed on the p-scale to avoid the use of negative exponents or preceding zeroes.Objective
-
•Determine [H3O1+], [OH1–], pH, and pOH of a solution of a strong acid or strong base of known concentration.
6.2-1. Method for Converting to the p-Scale
The p-scale is defined in Equation 6.2. A 'p' placed before a concentration or a constant means that the number is the negative log of the concentration or constant. For example, pH = –log [H3O1+] and pKa = –log Ka. Taking the antilogarithm of both sides of Equation 6.2 gives the expression for converting the p-scale to the concentration or constant. The hydronium ion concentration in a solution with pH = 3.20 is [H3O1+] = 10–pH = 10–3.20 = 6.3e–04 and an acid with a pKa = 5.62 has a Ka = 10–5.62 = 2.4e–06. It might appear that the [H3O1+] and Ka do not have the correct number of significant figures. After all, the pH has three, while the [H3O1+] and Ka each have only two. The difference arises because the numbers to the left of the decimal in a logarithm indicate the exponent, not the significant figures. This is due to the way negative exponents are handled. An exponent of –3.20 is expressed as 0.80 – 4, so 10–3.20 = (100.80)(10–4) = (6.3)(10–4). Thus, the significant figure, 6.3, is determined from 0.80, which comes from the 0.20 in the pH. The exponent, –4, is dictated by the number to the left of the decimal. We conclude that significant figures can be lost when converting from pX to X, while they can be gained in going from X to pX. This is the reason that pKa values are usually reported to three significant figures, while Ka values have only two. The following are common uses of the p-scale.| pH = –log [H3O1+] | [H3O1+] = 10–pH |
| pOH = –log [OH1– ] | [OH1– ] = 10–pOH |
| pKw = –log(Kw) = –log(1.0 × 10 |
Kw = 10–pKw = 10–14 |
| pKa = –log(Ka) | Ka = 10–pKa |
Table 6.1
6.2-2. pKw, pH, and pOH
We now express the ion product for water (Equation 6.1Kw = [H3O1+][OH1−] = 1.0 × 10−14 at 25 °C
) in terms of pH and pOH.
Kw = [H3O1+][OH1−]
−log Kw = −log [H3O1+] − log [OH1−]
| T (°C) | pKw | Kw |
|---|---|---|
| 0 | 14.94 | 1.15e–15 |
| 25 | 14.00 | 1.00e–14 |
| 50 | 13.28 | 5.25e–15 |
| 75 | 12.71 | 1.95e–13 |
| 100 | 12.26 | 5.50e–13 |
Table 6.2: pKw at Selected Temperatures
6.2-3. pH, Acidity, Basicity, and Neutrality
Acidic solutions: [H3O1+] > 1.0 × 10–7. Taking the negative logarithm of both sides of this inequality producespH < 7.00 for acidic solutions. A solution in which [H3O1+] = 1.0 M (pH = 0.0) is fairly acidic solution, so most pH values for acidic solutions lie between 0 and 7. However, H3O1+ concentrations greater than 1.0 M are possible. We conclude that the pH of a solution decreases as the acidity increases, and the pH of most acidic solutions lies between 0 and 7, but negative values are possible. Basic Solutions: [OH1–] > 1.0 × 10–7, so [H3O1+] < 1.0 × 10–7. Taking the negative logarithm of both sides yields pOH < 7 or pH > 7 for basic solutions. A solution in which [OH1–] = 1.0 M has a pOH = –log(1.0) = 0.0, which gives it a pH = 14.0 – 0.0 = 14.0, which is a very basic solution. However, solutions in which [OH1–] > 1 M are not uncommon. We conclude that the pH of a solution increases as the basicity increases, and the pH of most basic solutions lie between 7 and 14, but values higher than 14 are possible. Neutral Solutions: [H3O1+] = [OH1–] = 1.0 × 10–7, so pH = pOH = 7.00 (at 25 °C). Thus, a neutral solution at
25 °C is one with pH = 7.00. These conclusions are summarized in the following figure.
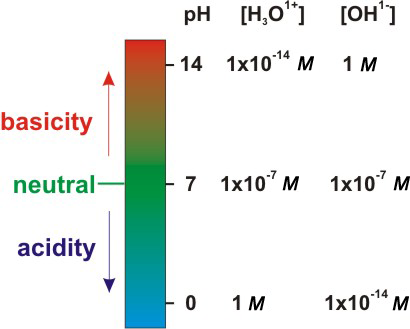
Figure 6.2: pH and Solution Type at 25 °C
Pictured above is the relationship between pH, acidity, and basicity.
6.2-4. Converting to the p-Scale Exercises
Exercise 6.2:
Determine the pH and pOH of the following solutions.
| Concentration | pH | pOH |
|---|---|---|
| [H3O1+] = 1.0e–07 M |
7.00_0_3_
pH = [H3O1+] = –log(1.0e–7) = 7.00
|
7.00_0_3_
pOH = 14.00 – pH = 14.00 – 7.00 = 7.00
|
| [H3O1+] = 0.042 M |
1.38_0_3_
pH = [H3O1+] = –log(0.042) = 1.38
|
12.62_0_4_
pOH = 14.00 – pH = 14.00 – 1.38 = 12.62
|
| [OH1–] = 0.50 M |
13.70_0_4_
pH = 14.00 – pOH = 14.00 – 0.30 = 13.70
|
0.30_0_2_
pOH = –log[OH1–] = –log(0.50) = 0.30
|
6.2-5. Exercise
Exercise 6.3:
What are [H3O1+] and [OH1–] in a solution with a pH of 8.62?
[H3O1+] =
2.4e-9_0__
[H3O1+] = 10–pH = 10–8.62 = 2.4e–09
M

pOH =
5.38_0__
pOH = 14.00 – pH = 14.00 – 8.62 = 5.38

[OH1–] =
4.2e-6_0__

[OH1−] = 10−pOH = 10−5.38 = 4.2e−06 or
[OH1−] =
=
= 4.2e−06 M
M
| Kw |
| [H3O1+] |
| 1.0e−14 |
| 2.4e−09 |
6.2-6. Exercise
Exercise 6.4:
The pH of a sample of lemon juice is found to be 2.32. What are the hydronium and hydroxide ion concentrations?
[H3O1+] =
4.8e-3_0__
[H3O1+] = 10–pH = 10–2.32 = 4.8e–03 M
M

pOH =
11.68_0__
pOH = 14.00 – pH = 14.00 – 2.32 = 11.68

[OH1–] =
2.1e-12_0__

[OH1−] = 10−pOH = 10−11.68 = 2.1e−12 M or
[OH1−] =
=
= 2.1e−12 M
M
| Kw |
| [H3O1+] |
| 1.0e−14 |
| 4.8e−03 |
6.2-7. Exercise
Exercise 6.5:
The hydroxide ion concentration in a bottle of household ammonia is 0.0083 M. Determine the pH, pOH, and the hydronium ion concentration of the solution.
pOH =
2.08_0__
pOH = –log [OH1–] = –log(0.0083) = 2.08

pH =
11.92_0__
pH = 14.00 – pOH = 14.00 – 2.08 = 11.92

[H3O1+] =
1.2e-12_0__

[H3O1+] = 10−pH = 10−11.92 = 1.2e−12 M or
[H3O1+] =
=
= 1.2e−12 M
M
| Kw |
| [OH1−] |
| 1.0e−14 |
| 0.00831.2e−12 M |
6.3 Strong Acids
Introduction
The common strong acids are HClO4, HCl, HBr, HI, HNO3, and H2SO4. In this section, we discuss how the pH of a strong acid solution is determined.Objective
-
•Calculate the pH of the solutions of strong acids and of strong bases.
6.3-1. Strong Acid Video
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•View the video full screen in another window.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
6.3-2. Strong Acid Solutions
Hydrochloric acid is a strong acid, so essentially all of the HCl reacts. The reaction is so extensive that it is usually represented with a single arrow.| HCl | + | H2O | → | H3O1+ | + | Cl1– | |
|---|---|---|---|---|---|---|---|
| initial | co | 0 | 0 | ||||
| Δ | –co | +co | co | ||||
| eq | 0 | co | co |
6.3-3. Exercises
Exercise 6.6:
What is the pH of a 0.16 M solution of hydrochloric acid?
pH =
0.80_0_2_
[H3O1+] = co, so pH = –log(co) = –log(0.16) = 0.80

6.4 Weak Acids
Introduction
Weak acids react only slightly with water, so the hydronium ion concentration in a solution of a weak acid does not equal the makeup concentration. In this section, we show how to determine the concentrations of all of the species in a solution of a weak acid.Objectives
-
•Write the Ka expression for a weak acid.
-
•Determine the equilibrium concentrations of all species present in and the pH of solutions of weak acids.
-
•Determine the pH, Ka, or initial concentration of a weak acid solution given the other two.
-
•Calculate the percent ionization of a weak acid.
-
•Convert between pKa and Ka.
6.4-1. Weak Acid Video
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•View the video full screen in another window.
-
•View the video in text format by scrolling down.
6.4-2. Weak Acid-Water Reaction Table
The equilibrium constant for the reaction of an acid and water is called the acid dissociation constant, Ka. Ka is so large for strong acids that all of the acid reacts to produce hydronium ion and the conjugate base of the acid. Ka is small for weak acids, so only a portion of a weak acid reacts with water. Thus, the Δ line entries of the reaction table are unknown. Consider the reaction of a generic weak acid HA with water.| HA | + | H2O | ⇌ | H3O1+ | + | A1– | |
|---|---|---|---|---|---|---|---|
| initial | co | 0 | 0 | ||||
| Δ | –x | x | x | ||||
| initial | co – x | x | x |
6.4-3. Solving the Ka Expression
We must solve Equation 6.5 for x to obtain the equilibrium concentrations in an aqueous solution of the weak acid HA.Ka =
| x2 |
| co − x |
Ka =
| x2 |
| co |
6.4-4. Five Percent Rule
Equation 6.6 is an easy way to determine the concentrations in a solution of a weak acid, but the approximation used to derive it is not always valid, so the answer should always be checked. There are two ways to check whether x is negligible:-
•Inspection: The value of x calculated with Equation 6.6[H3O1+] = [A1−] =is often so small that it is obviously negligible compared to co. For example, if co = 0.100 M and x = 0.0000001 M then co – x = 0.100 M and the assumption is good.

Kaco -
•5% Rule: If x is less than 5% of co, then approximating co for co – x will produce the same answer as the quadratic formula. For example, substitution of co = 0.100 and Ka = 1.6e–04 into Equation 6.6[H3O1+] = [A1−] =gives x = 0.004 M. In this case, co – x = 0.100 – 0.004 = 0.096, which is not equal to co. However, (x/co) = 0.04, which is 4%. Thus, x is less than 5%, so using the quadratic formula would result in the same answer for x.

Kaco
6.4-5. Solving Without Approximation
If the answer produced by Equation 6.6[H3O1+] = [A1−] =
is greater than 5% of co, the terms in Equation 6.5 | Kaco |
Ka =
=
=
must be gathered in the form of a quadratic equation | [H3O1+][A1−] |
| [HA] |
| (x)(x) |
| co − x |
| x2 |
| co − x |
(ax2 + bx + c = 0)
and solved with the quadratic formula given below.
However, Equation 6.6[H3O1+] = [A1−] =
is so easy to use, that it is usually simpler to use it and check to be certain that x is within the 5% limit. This is especially true since most of the acids and concentrations we deal with in this course are so weak that the 5% rule is usually obeyed. However, for the stronger of the weak acids or for very dilute solutions, more than 5% of the acid may react, so always check.
 | Kaco |
6.4-6. Method for Weak Acid Problems
Equations 6.5Ka =
=
=
and 6.6| [H3O1+][A1−] |
| [HA] |
| (x)(x) |
| co − x |
| x2 |
| co − x |
[H3O1+] = [A1−] =
indicate that three terms (co, x, and Ka) are required to establish a weak acid equilibrium. Consequently, there are three different types of problems that are solved using these equations. The three differ in the identity of the unknown.
 | Kaco |
-
•x: What is the pH, [H3O1+], or [A1–]? Given: Ka (or the identity of the acid so you can look it up) and the makeup concentration. Method: Use Equation 6.6[H3O1+] = [A1−] =to solve for the unknown then check that x is indeed small enough to neglect. If x is not small enough, rearrange the expression so that it is in the form of a quadratic equation and use the quadratic formula to solve for the unknown concentration.

Kaco -
•Ka: What is the value of Ka? Given: x as the pH, [H3O1+], or [A1–] and the makeup concentration. Method: Substitute the known values into Equation 6.5Ka =. Since x and co are known, there is no reason to make the neglect-x approximation, so make the subtraction.
=[H3O1+][A1−] [HA]
=(x)(x) co − x x2 co − x -
•co: How much acid must be used to make a solution? Given: x as pH, [H3O1+], or [A1–], and Ka (or the identity of the acid so you can look it up). Method: Solve Equation 6.5Ka =for the equilibrium concentration of the weak acid (co – x), then solve for co using the given value of x.
=[H3O1+][A1−] [HA]
=(x)(x) co − x x2 co − x
6.4-7. Determining the pH Exercise
Exercise 6.7:
First, look up the Ka of acetic acid in the resource titled Acid-Base Table with pKa.
Ka =
1.8e-5_0__
The tabulated Ka of acetic acid is 1.8e–5.

Then use Equation 6.6
[H3O1+] = [A1−] =
with the Ka and the given initial concentration to determine x = [H3O1+]. | Kaco |
[H3O1+] =
0.0013_0__
Use Ka = 1.8e–05 and Equation 6.6: H3O1+] = (coKa)1/2 = 0.0013 M.
Check approximation: 0.10 – 0.0013 = 0.10 M. Approximation is valid. Alternatively, 0.0013/0.10 = 0.013, so the acid is only 1.3% dissociated, which is less than 5%, so the approximation is valid. M
Check approximation: 0.10 – 0.0013 = 0.10 M. Approximation is valid. Alternatively, 0.0013/0.10 = 0.013, so the acid is only 1.3% dissociated, which is less than 5%, so the approximation is valid. M
Finally, convert [H3O1+] into pH.
pH =
2.87_0__
pH = –log [H3O1+]

6.4-8. Determining the pH Exercise
Exercise 6.8:
What is the pH of a 0.080-M solution of ammonium nitrate? Ammonium ion is a weak acid.
(The relevant pKa can be found in the Acid-Base Table with pKa.)
NH41+ + H2O ⇌ H3O1+ + NH3
[H3O1+] =
6.7e-6_0__
Use Equation 6.6: [H3O1+] = (coKa)1/2 = 6.7e–6 M, which is certainly negligible compared to 0.080 M.
M

pH =
5.17_0__
pH = –log [H3O1+]

6.4-9. Determining Ka Exercise
Exercise 6.9:
If a 0.0750-M solution of formic acid has a pH of 2.447, what is the Ka of formic acid?
The equilibrium concentrations are as follows.
CHOOH + H2O ⇌ CHOO1– + H3O1+
[H3O1+] =
0.00357_0__
[H3O1+] = 10–pH = 10–2.447 = 0.00357 M
M

[CHOO1–] =
0.00357_0__
[CHOO1–] = [H3O1+] = 0.00357 M
M

[CHOOH] =
0.0714_0__
[CHOOH] = co – x = 0.0750 – 0.00357 = 0.0714 M
M

Ka =
1.79e-4_0__

Ka =
=
| [H3O1+][CHOO1−] |
| [CHOOH] |
| (0.00357)2 |
| 0.0714 |
6.4-10. Determining the Makeup Concentration Exercise
Exercise 6.10:
What initial concentration of a KHSO4 solution would be required to make a pH = 2.00 solution?
(The relevant pKa can be found in the Acid-Base Table with pKa.)
HSO41– + H2O ⇌ SO42– + H3O1+
The equilibrium concentrations are as follows.
[H3O1+] =
0.010_0_2_
[H3O1+] = 10–pH = 10–2.00
M

[SO42–] =
0.010_0_2_
[SO42–] = [H3O1+]
M

[HSO41–] =
0.0083_0__

HSO41− =
=
= 8.3e−3 M
M
| [SO42−][H3O1+] |
| Ka |
| (0.010)(0.010) |
| 0.012 |
co =
0.018_0__
The initial concentration equals the equilibrium concentration plus the concentration of the species formed in the reaction co = [HSO41–] + x = 0.0083 + 0.010 = 0.018 M.

6.4-11. Percent Ionization
We now show that the fraction of an acid that reacts depends upon both its concentration and its acid dissociation constant. We start by reproducing the equilibrium line in the reaction table for a weak acid reacting with water.| HA | + | H2O | ⇌ | H3O1+ | A1– | ||
|---|---|---|---|---|---|---|---|
| eq | co – x | x | x |
[H3O1+] = [A1−] =
to determine x as (coKa)1/2. Substitution of this value of x into the expression for the fraction that reacts produces the following.
 | Kaco |
fraction dissociating =
=
=
| x |
| co |
| ||
| co |
 |
|
| Molarity | HNO2 | CH3COOH | HOCl |
|---|---|---|---|
| 1.0 | 2.0% | 0.42% | 0.019% |
| 0.10 | 6.1%* | 1.3% | 0.059% |
| 0.010 | 18%* | 4.2% | 0.19% |
| 0.00010 | 83%* | 34%* | 1.9% |
Table 6.3: Percent Ionization of Selected Acids
*The percent ionization exceeds 5% in these cases, so the quadratic formula was used to determine x.
6.4-12. Percent Ionization Exercise
Exercise 6.11:

What is the percent ionization and pH of 0.026 M HF? (The relevant pKa can be found in the Acid-Base Table with pKa.)
HF + H2O ⇌ F1– + H3O1+
Ka =
% dissociation using Equation 6.7
% dissociation using Equation 6.7
percent ionization =
× 100%
=  |
|
17_0__
× 100% = 17%
%

 |
|
-
Is Equation 6.7
-
Yes The dissociation exceeds 5%, so the equation is not valid.
-
No
percent ionization =
× 100%
valid for this solution?
 |
|

[H3O1+] using the quadratic formula =
% dissociation =
pH =
4.0e-3_0_2_
Setup the Ka expression.
Gather terms in the form of a quadratic equation.
Use a = 1, b = 7.2e–4, and c = –1.87e–5 in the quadratic formula. The concentration cannot be negative, so only the plus operator is used with the squareroot to obtain [H3O1+] = 0.0040 M. M
7.2e−4 =
| x2 |
| 0.026 − x |
Gather terms in the form of a quadratic equation.
x2 + 7.2e−4x − 1.87e−5 = 0
Use a = 1, b = 7.2e–4, and c = –1.87e–5 in the quadratic formula. The concentration cannot be negative, so only the plus operator is used with the squareroot to obtain [H3O1+] = 0.0040 M. M
% dissociation =
15_0__

% =
× 100% = 15%
%
| 0.0040 M |
| 0.026 M |
pH =
2.40_0_3_
pH = –log(0.0040) = 2.40

6.5 Polyprotic Acids
Introduction
Polyprotic acids contain two or more protons. For example, H2S is diprotic and H3PO4 is triprotic. There are some polyprotic acids that contain more than three protons, but we will not consider any of these acids. The conjugate base of a polyprotic acid is also an acid, and the solution of a polyprotic acid is really a solution of more than one acid. Although it might seem that this would make the treatment of these acids very difficult, determining the concentrations of the species present in a polyprotic acid is not much different than determining the concentrations in a solution of a monoprotic acid.Objective
-
•Determine the concentrations of all species in a solution of a polyprotic acid of known concentration.
6.5-1. Phosphoric Acid Overview
We examine a 0.10-M solution of phosphoric acid as an example because it contains three protons and is the most complicated. The three deprotonation steps are the following.| H3PO4 + H2O ⇌ H2PO41– + H3O1+ | K1 = 7.5 × 10–5 |
| H2PO41– + H2O ⇌ HPO42– + H3O1+ | K2 = 6.2 × 10–8 |
| HPO42– + H2O ⇌ PO43– + H3O1+ | K3 = 4.8 × 10–13 |
Note that each K value is over 1,000 times smaller than the preceding value. This is the case for most polyprotic acids, and it is why polyprotic acids can be treated in a relatively simple manner. The large decrease in K means that a negligible amount of each acid reacts in each step, so the concentration of any species is the concentration determined in the first step in which it is produced. The method we will use to find the concentrations of all species is the following:
-
1Determine [H3O1+], [H2PO41–], and [H3PO4] from the first acid dissociation. These concentrations are not affected by subsequent steps because the subsequent equilibrium constants are so small.
-
2Set up the reaction table for the second reaction using the [H3O1+] and [H2PO41–] determined in step 1 as the initial conditions. Solve the equilibrium problem for [HPO42–], which will be shown to equal K2.
-
3Set up the reaction table for the third reaction using [H3O1+] and [HPO42–] determined in steps 1 and 2 as initial concentrations. Solve the equilibrium problem for [PO43–].
6.5-2. Phosphoric Acid Step 1
Essentially all of the hydronium ion in a solution of a polyprotic acid is produced in the first deprotonation step.
| H3PO4 | + | H2O | ⇌ | H2PO41– | + | H3O1+ | K1 = 7.5 × 10–3 | |
|---|---|---|---|---|---|---|---|---|
| initial | 0.10 | 0 | 0 | M | ||||
| Δ | –x | +x | +x | M | ||||
| eq | 0.10 – x | x | x | M |
x = (coKa)1/2 = {(0.10)(7.5e−3)}1/2 = 0.027 M
1
Set up the Ka expression.
7.5e−3 =
| x2 |
| 0.10 − x |
2
Multiply both sides by (0.10 – x) to get x out of the denominator.
(7.5e−3)(0.10 − x) = x2
3
Carry out the multiplication on the left side.
7.5e−4 − 7.5e−3x = x2
4
Gather terms in the form of a quadratic equation.
x2 + 7.5e−3x − 7.5e−4 = 0
5
Compare the above to the quadratic equation to obtain the following.
a = 1, b = 7.5e−3, and c = −7.5e−4
6
Use these values in quadratic formula to obtain the following.
x = [H3O1+] = [H2PO41−] = 0.024 M
7
Use [H3PO4] = co – x to obtain the following.
[H3PO4] = 0.10 − 0.02 = 0.08 M
6.5-3. Phosphoric Acid Step 2
The reaction table for the second deprotonation step is the same as that for the dissociation of 0.024 M H2PO41– except that the initial concentration of [H3O1+] is also 0.024 M as a result of the dissociation of H3PO4.| H2PO41– | + | H2O | ⇌ | HPO42– | + | [H3O1+] | K2 = 6.2 × 10–8 | |
|---|---|---|---|---|---|---|---|---|
| initial | 0.024 | 0 | 0.024 | M | ||||
| Δ | –x | 0 | +x | M | ||||
| eq | 0.024 – x | x | 0.024 + x | M |
Ka =
| [HPO42−][H3O1+] |
| [H2PO41−] |
6.2e−8 =
| x(0.024 + x) |
| 0.024 − x |
The concentration of the ion produced in the second deprotonation of a polyprotic acid equals K2, the equilibrium constant for the deprotonation.
6.5-4. Phosphoric Acid Step 3
The reaction table for the third deprotonation step is the same as dissociation of HPO42– except that the initial concentration of [H3O1+] is 0.024 M from the first step and that of H2PO41– is 6.2e–8 M as a result of the second step.| HPO42– | + | H2O | ⇌ | PO43– | + | [H3O1+] | K3 = 4.8 × 10–13 | |
|---|---|---|---|---|---|---|---|---|
| initial | 6.2e–8 | 0 | 0.024 | M | ||||
| Δ | –x | +x | +x | M | ||||
| eq | 6.2e–8 | x | 0.024 | M |
K3 =
| [PO43−][H3O1+] |
| [HPO42−] |
4.8e−13 =
| x(0.024) |
| (6.2e−8) |
[PO43−] =
= 1.2e−18 M
| (4.8e−13)(6.2e−8) |
| (0.024) |
-
•[H3PO4] = 0.08 M
-
•[H2PO41–] = 0.024 M
-
•[HPO42–] = 6.2e–8 M
-
•[PO43–] = 1.2e–18 M
6.5-5. Hydrogen Sulfide Exercise
Exercise 6.12:
A saturated solution of hydrogen sulfide is 0.10 M at 1 atm and 25 °C. What are the concentrations of all species present in a saturated H2S solution? (K1 = 1.0e-7 and K2 = 1.3e-13.)
First, determine the concentrations of the species involved in the first reaction. Use "x" as the unknown identifier, and assume that it is negligible compared to 0.10 M on the "eq" line.
| H2S | + | H2O | ⇌ | HS1– | + | H3O1+ | K1 = 1.0e–07 | |
|---|---|---|---|---|---|---|---|---|
| initial |
0.10_0_2_
The initial concentration of H2S is given as 0.10 M.
|
0_0__
There is no HS1– until the reaction takes place.
|
0_0__
Assume that there is no H3O1+ until the reaction takes place.
|
M | ||||
| Δ |
o_-x_s
H2S disappears.
|
o_+x_s
HS1– increases by the same amount that H2S decreases. Include the sign.
|
o_+x_s
H3O1+ increases by the same amount that H2S decreases. Include the sign.
|
M | ||||
| eq |
0.10_0_2_
The amount of H2S that reacts is negligible.
|
o_x_s
Sum the Δ and eq lines. Use no sign.
|
o_x_s
Sum the Δ and eq lines. Use no sign.
|
M |
[HS1–] =
1.0e-4_0_2_
Use Equation 6.6: [HS1–] = {(0.10)(1.0e–07)}1/2 = 1.0e–04 M.
M

[H3O1+] =
1.0e-4_0_2_
[H3O1+] = [HS1–] = 1.0e–04 M
M

[H2S] =
0.10_0_2_
x is negligible, so [H2S] = 0.10 M.
M

Next, determine the concentration of the species formed in the second reaction. Use "y" as the unknown identifier, and assume it is negligible on the "eq" line.
| HS1– | + | H2O | ⇌ | S2– | + | H3O1+ | K2 = 1.3e–13 | |
|---|---|---|---|---|---|---|---|---|
| initial |
1.0e-4_0_2_
The initial concentration of HS1– is the equilibrium concentration found above.
|
0_0__
There is no S2– until the reaction takes place.
|
1.0e-4_0_2_
The initial concentration of H3O1+ is the equilibrium concentration found above.
|
M | ||||
| Δ |
o_-y_s
HS1– disappears.
|
o_+y_s
S2– increases by the same amount that HS1– decreases. Include the sign.
|
o_+y_s
H3O1+ increases by the same amount that HS1– decreases. Include the sign.
|
M | ||||
| eq |
1.0e-4_0_2_
The amount of HS1– that reacts is negligible.
|
o_y_s
Sum the Δ and eq lines. Use no sign.
|
1.0e-4_0_2_
Sum the Δ and eq lines. Use no sign.
|
M |
[S2–] =
1.3e-13_0__
S2– ion is the ion produced in the second step, [S2–] = K2 = 1.3e–13 M.
M

6.5-6. Carbonic Acid Exercise
Exercise 6.13:
Determine the pH and the concentrations of all carbon containing species in 0.18 M H2CO3 solution.
H2CO3 + H2O ⇌ HCO31– + H3O1+ K1 = 4.3e–7
HCO31– + H2O ⇌ CO32– + H3O1+ K2 = 4.7e–11
HCO31– + H2O ⇌ CO32– + H3O1+ K2 = 4.7e–11
[H2CO3] =
0.18_0__
x is negligible.
M

[HCO31–] =
2.8e-4_0__

Use [H3O1+] = [A1−] =
M
 | Kac0 |
[H3O1+] =
2.8e-4_0__
[H3O1+] ⇌ [HCO31–]
M

pH =
3.56_0__
pH = –log [H3O1+]

[CO32–] =
4.7e-11_0__
CO32– ion is the ion produced in the second step.
M

6.5-7. Sulfuric Acid Exercise
Exercise 6.14:
What are the H3O1+, HSO41–, and SO42– concentrations in 0.10 M sulfuric acid?
Sulfuric acid is a strong acid and its conjugate base (hydrogen sulfate ion) is one of the strongest weak acids, so this exercise is a little different.
H2SO4 + H2O → HSO41– + H3O1+ extensive
HSO41– + H2O ⇌ SO42– + H3O1+ K = 0.012
HSO41– + H2O ⇌ SO42– + H3O1+ K = 0.012
After the extensive deprotonation of H2SO4:
[H3O1+] =
0.10_0_2_
H2SO4 is a strong acid.
M

[HSO41–] =
0.10_0_2_
H2SO4 is a strong acid.
M

Assume the amount of HSO41– that reacts in the second step is negligible.
SO42– =
0.012_0__
Sulfate ion is the second ion produced, so its concentration would equal K if x were negligible.
M

However, that would require a 12% reaction, so the amount that reacts is not negligible. Use the quadratic formula to obtain the equilibrium concentrations.
[SO42–] =
0.0098_0__
The neglect-x assumption is not valid, so the equation must be rearranged and the quadratic formula must be used.
Multiply both sides by (0.10 – x) to eliminate the denominator, and gather terms to put the resulting equation into the form appropriate for the quadratic formula.
Apply the quadratic formula to obtain the value of x = [SO42–].

Ka = 0.012 =
=
| [H3O1+][SO42−] |
| [HSO41−] |
| (0.10 + x)(x) |
| (0.10 − x) |
Multiply both sides by (0.10 – x) to eliminate the denominator, and gather terms to put the resulting equation into the form appropriate for the quadratic formula.
x2 + 0.112x − 0.0012 = 0
Apply the quadratic formula to obtain the value of x = [SO42–].
x =
= 0.0098 M
M
−0.112 +
| ||
| 2 |
[HSO41–] =
0.09_0__
[HSO41–] = 0.10 – x = 0.10 – 0.01 = 0.09 M
M

[H3O1+] =
0.11_0__
[H3O1+] = 0.10 + x = 0.10 + 0.01 = 0.11 M
M

6.6 Strong Bases
Introduction
The solutions of strong bases are usually made by dissolving metal hydroxides in water. In this section, we discuss how the pH of a strong base solution is determined.Objective
-
•Calculate the pH of the solutions of strong bases.
6.6-1. Strong Base Solutions
Dissolving a metal hydroxide in water is represented by the following chemical equation.M(OH)n → Mn+ + nOH1−
6.6-2. Exercise
Exercise 6.15:
What is the pH of a solution labeled 0.16 M Ba(OH)2 at 25 °C? pH cannot be determined directly for a base, so we can either convert the hydroxide ion concentration to a hydronium concentration and then determine the pH, or we can convert the hydroxide ion concentration to a pOH and then to a pH. We choose the latter.
OH1– =
0.32_0__
[OH1–] = nco = 2(0.16) = 0.32 M
M

pOH =
0.49_0__
pOH = –log [OH1–] = –log(0.32) = 0.49

pH =
13.51_0__
H = 14.00 – pOH = 14.00 – 0.49 = 13.51

6.7 Weak Bases
Introduction
Weak bases are treated in a manner identical to that used for weak acids.Objectives
-
•Write the Kb expression for a weak base.
-
•Determine the equilibrium concentrations of all species present in and the pH of solutions of weak bases.
-
•Determine the pH, Kb, or initial concentration of a weak base solution given the other two.
-
•Convert between pKb and Kb.
-
•Convert between the Ka and Kb of a conjugate acid-base pair.
6.7-1. Weak Base-Water Reaction
The equilibrium constant for the reaction of a base and water has the symbol, Kb. Kb is small for weak bases, so only a portion of a weak base reacts with water. Thus, the Δ line entries of the reaction table are unknown. Consider the reaction of a generic weak base A1– with water.| A1– | + | H2O | → | OH1– | + | HA | |
|---|---|---|---|---|---|---|---|
| initial | co | 0 | 0 | ||||
| Δ | –x | x | x | ||||
| initial | co – x | x | x |
Kb =
| x2 |
| co |
6.7-2. Relating Ka and Kb
Consider the product of the Ka of HA (a weak acid) and the Kb of A1– (its conjugate base).(Ka)(Kb) =
×
| [H3O1+][A1−] |
| [HA] |
| [OH1−][HA] |
| [A1−] |
(Ka)(Kb) = [H3O1+][OH1−]
6.7-3. Weak Base pH Exercise
Exercise 6.16:
What is the pH of a solution that is 0.12 M in NO21–? (The relevant pKa can be found in the Acid-Base Table with pKa.)
Kb =
2.5e-11_0__
Ka of HNO2 = 4.0e–04, so 
Kb =
= 2.5e−11
| 1.0e−14 |
| 4.0e−04 |
[OH–1] =
1.7e-6_0__
Use Equation 6.9: [OH1–] = {(2.5e–11)(0.12)}1/2 = 1.7e–06 M
M

pOH =
5.76_0__
pOH = –log [OH1–] = –log(1.7e–06) = 5.76

pH =
8.24_0__
pH = pKw – pOH = 14.00 – 5.76 = 8.24

6.7-4. pKa and pKb
Acid and base constants are frequently given on the p-scale as follows. Due to the minus sign in the definition, a higher pKa or pKb indicates a weaker acid or base. Taking the negative logarithm of both sides of Equation 6.10KaKb = Kw
produces the following relationship.
6.7-5. Determining Kb Exercise
Exercise 6.17:
The pH of a 0.085-M solution of methylamine is 11.77. What are the Kb of methylamine (CH3NH2) and the pKa of CH3NH31+, its conjugate acid?
[OH1–] =
5.9e-3_0__
pOH = pKw – pH = 14.00 – 11.77 = 2.23
[OH1–] = 10–pOH = 10–2.23 = 5.9e–03 M M
[OH1–] = 10–pOH = 10–2.23 = 5.9e–03 M M
[CH3NH31+] =
5.9e-3_0__
[CH3NH31+] = [OH1–]
M

[CH3NH2] =
0.079_0__
[CH3NH2] = co – x = 0.085 – 0.006 = 0.079 M
M

Kb =
4.4e-4_0__

Kb =
=
= 4.4e−04
| [OH1−][CH3NH31+] |
| [CH3NH2] |
| (5.9e−03)(5.9e−03) |
| 0.079 |
pKa of CH3NH31+ =
10.64_0__
pKb = –log(4.4e–4) = 3.36
pKa = 14.00 – pKb = 14.00 – 3.36 = 10.64
pKa = 14.00 – pKb = 14.00 – 3.36 = 10.64
6.7-6. pKa, pKb, Ka, and Kb Exercise
Exercise 6.18:
Lactic acid is usually prepared by fermentation of starch, cane sugar, or whey. Large amounts of lactic acid in muscle lead to fatigue and can cause cramps. Lactic acid, generated in milk by fermentation of lactose, causes milk to sour. Lactic acid is used in the preparation of cheese, soft drinks, and other food products. Its stucture is given below. The proton with a circle around it is the acidic proton.
 The pKa of lactic acid is 3.89.
The pKa of lactic acid is 3.89.

Ka of lactic acid =
1.3e-4_0__
Ka = 10–pKa = 10–3.89

pKb of lactate ion =
10.11_0__
pKb = pKw – pKa = 14.00 – 3.89

Kb of lactate ion =
7.8e-11_0__
Kb = 10–pKb = 10–10.11

6.7-7. Bases of Polyprotic Acids
Bases that can accept more than one proton are treated much the same way as polyprotic acids. Consider the case of the sulfide ion, which can accept two protons.-
1S2– + H2O ⇌ HS1– + OH1– K1 = 0.077
-
2HS1– + H2O ⇌ H2S + OH1– K2 = 1.0 × 10–7
6.7-8. Base of a Polyprotic Acid Exercise
Exercise 6.19:
What is the pH of 0.064 M sulfide ion? (The relevant pKa can be found in the Acid-Base Table with pKa.)
Kb =
0.077_0__
Use 
KaKb = Kw
and the tabulated Ka of the conjugate acid.
[OH1–] =
0.042_0__
The quadratic equation that must be solved is x2 + 0.077x – 0.0049 = 0.

using quadratic formula if assumption is not valid.
pOH =
1.38_0__
pOH = –log(0.042)

pH =
12.62_0__
pH = 14.00 – pOH at 25 °C

6.8 Salts of Weak Acids and Bases
Introduction
Salts are ionic compounds that are produced in acid-base reactions. The anion of the salt is the conjugate base of the reacting acid, and the cation is usually a metal ion that was associated with the reacting base. For example, the reaction between NaOH and HCl is the acid-base reaction between H3O1+ and OH1–. Na1+ ion, the metal ion associated with the reacting base and Cl1–, the conjugate base of the reacting acid serve as spectator ions. Combination of the spectator ions produces a salt, NaCl. Salts can be acidic, basic, or neutral depending upon the relative acidity/basicity of the cation and anion. In this section, we discuss the acid-base properties of salts.Objective
-
•Define the term salt and predict whether a salt is neutral, basic, or acidic.
6.8-1. Acid-Base Properties of Cations and Anions
Small, highly-charged metal cations have orbitals available to accept electron pairs to form covalent bonds, so they are Lewis acidic. However, the available orbitals of the 1A metal ions are so high in energy that these ions are not acidic in aqueous solutions. Thus, 1A metal ions do not impact the acidity or basicity of a salt. For simplicity, we will limit our use of metal ions to 1A metal ions. The only other common cation is NH41+, which is acidic. Most anions readily accept the positive charge of a proton, so anions are usually good bases. The exceptions are the conjugate bases of the strong acids (ClO41–, Cl1–, Br1–, I1–, and NO31–), which are neutral, and the protonated anions (HSO41–, HSO31– and H2PO41–), which are acidic.6.8-2. Acid-Base Properties of Salts
A salt can be acidic, basic, or neutral depending upon the relative acid and base strengths of the cation and anion.-
1Neutral Salts: The reaction of a strong acid and a strong base produces a neutral salt. The cation in such reactions is a 1A metal and the anion is the conjugate base of a strong acid. Thus, both ions are neutral, which produces a neutral salt. The salt of a weak acid and a weak base can be neutral only when the Ka of the cation equals the Kb of the anion. Ammonium acetate is a neutral salt formed in the reaction of acetic acid and ammonia. It is neutral because the Ka of the ammonium ion equals the Kb of the acetate ion.
-
2Basic Salts: Basic Salts are produced in the reaction between a weak acid and a strong base. For example, NaCN is a basic salt that is produced by the reaction of HCN and NaOH. It is basic because sodium ion does not impact the acid-base properties, while the cyanide ion is a basic anion. Basic salts are produced in the reaction between a weak acid and a weak base if the Kb of the base is greater than the Ka of the acid. Ammonium sulfide is a basic salt because the Kb of the sulfide ion is greater than the Ka of the ammonium ion. Basic salts are the most common source of weak bases.
-
3Acidic salts: The reaction of a strong acid and a weak base produces acidic salts. NH4Cl is an acidic salt produced by the reaction between HCl and NH3. It is acidic because the ammonium ion is a weak acid, but chloride ion is the conjugate base of a strong acid, so it is not basic. Ammonium fluoride is acidic because the Ka of ammonium ion is greater than the Kb of the fluoride ion.
6.8-3. Predicting Salt Basicity and Acidity Exercise
Exercise 6.20:





Indicate whether a solution of each of the following salts is acidic, basic, or neutral.
-
KClO4
-
acidic The salt of a 1A metal and the conjugate base of a strong acid is neutral.
-
basic The salt of a 1A metal and the conjugate base of a strong acid is neutral.
-
neutral

-
Na2S
-
acidic The 1A metal ion is neutral, but sulfide is basic.
-
basic
-
neutral The 1A metal ion is neutral, but sulfide is basic.

-
NH4NO2
-
acidic
-
basic Ka(NH41+) = 5.6e–10 and Kb(NO21–) = 2.5e–11. Ka > Kb, so salt is acidic.
-
neutral Ka(NH41+) = 5.6e–10 and Kb(NO21–) = 2.5e–11. Ka > Kb, so salt is acidic.

-
(NH4)3PO4
-
acidic Ka(NH41+) = 5.6e–10 and Kb(PO43–) = 2.1e–2. Kb > Ka, so salt is basic.
-
basic
-
neutral Ka(NH41+) = 5.6e–10 and Kb(PO43–) = 2.1e–2. Kb > Ka, so salt is basic.

-
NH4C2H3O2
-
acidic Ka(NH41+) = 5.6e–10 and Kb(C2H3O2) = 5.6e–10. Kb = Ka, so salt is neutral.
-
basic Ka(NH41+) = 5.6e–10 and Kb(C2H3O2) = 5.6e–10. Kb = Ka, so salt is neutral.
-
neutral

6.8-4. Determining the pH of a Salt Exercise
Exercise 6.21:
What is the pH of a solution prepared by dissolving 3.5 g of KF (Mm = 58.1 g·mol–1) in sufficient water to make 150 mL of solution? (The relevant pKa can be found in the Acid-Base Table with pKa.)
Kb for F1– =
1.4e-11_0__
Ka(HF) = 7.2e–4 from the Acid-Base Table with pKw.

Kb =
= 1.4e−11
| 1.0e−14 |
| 7.2e−4 |
mol F1– =
0.060_0_2_

3.5 g KF ×
×
= 0.060 mol F1−
mol
| 1 mol KF |
| 58.1 g KF |
| 1 mol F1− |
| 1 mol KF |
[F1–] =
0.40_0_2_

[F1−] =
= 0.40 M
M
| 0.060 mol F1− |
| 0.15 L solution |
[OH1–] =
2.4e-6_0__
[OH1–] = (coKb)1/2; co = [F1–]
M

pOH =
5.63_0__
pOH = –log [OH1–] = –log(2.3664e–06) = 5.63. Note extra significant figures carried from the previous answer.

pH =
8.37_0__
pH = 14.00 – pOH = 14.00 – 5.63 = 8.37

6.9 Amphiprotic Salts
Introduction
Amphiprotic salts are both acids and bases, so their aqueous equilibria are slightly more complicated than those of weak acids or bases. In this section, we discuss the equilibria and give a simple expression for determining their pH.Objective
-
•Determine the pH of a solution of an amphiprotic salt.
6.9-1. Acid Equilibrium
As shown in the figure, HCO31– is an amphiprotic substance because it can behave as both an acid and a base.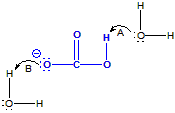
Figure 6.3: Amphiprotic Substances are Both Acids and Bases
HCO31– is amphiprotic because its acidic proton can be lost (arrow A) or a lone pair on the oxygen with negative formal charge can accept a proton (arrow B).
HCO31− + H2O ⇌ CO32− + H3O1+ Ka2 =
= 4.7e−11
| [CO32−][H3O1+] |
| [HCO31−] |
[OH1−]produced = [CO32−]
HCO31− + H2O ⇌ H2CO3 + OH1− Kb1 =
= 2.3e−8
| [H2CO3][OH1−] |
| [HCO31−] |
[OH1−]produced = [H2CO3]
[OH1−]produced = [H3O1+]consumed = [H2CO3]
[H3O1+] = [H3O1+]produced − [H3O1+]consumed = [CO32−] − [H2CO3]
