Chapter 9 – Electrochemistry

Introduction

Electron transfer, or redox, reactions form one of the broadest and most important classes of reactions in chemistry. All reactions involving oxygen, such as combustion and corrosion, are redox reactions. Photosynthesis, respiration, and the breakdown of food are biological processes that involve sequences of electron transfer reactions to transport and utilize energy from the sun. Electrochemistry is the marriage of electron transfer and electrical conductivity through a circuit, so all batteries are electrochemical devices. In this chapter, we review some of the topics introduced in Chapter 11 of CAMS, and extend our study of electron transfer to topics such as how concentrations affect cell potentials and how applied voltages can be used to plate one metal on another or to carry out non-spontaneous redox reactions.

9.1. Redox Review

Introduction

Electrochemistry was introduced in detail in CAMS Chapter 11, and a knowledge of that material is essential to the understanding of this chapter. While a brief summary is presented in this section, a more thorough background can be acquired by viewing the videos that can be found in the Sections of CAMS that are referenced in the following prerequisites. It is strongly recommended that you view these videos for a better review.

Prerequisites

•
CAMS 11.1-1 Introduction to Electron Transfer and Redox Reactions
•
CAMS 11.4-1 Standard Reduction Potentials
•
CAMS 11.5-1 Reactivity and Standard Reduction Potentials
•
CAMS 11.5-2 Writing Redox Chemical Equations

9.1-1. Definitions

•
During a redox reaction, electrons are transferred from an electron donor to an electron acceptor.
•
Donors lose electrons in a process known as oxidation, while the acceptors gain electrons in a process known as reduction.
•
Reactions involving oxidation and reduction are called redox reactions.
•
An acceptor cannot be reduced unless a donor is oxidized because electron transfer requires both a source and a destination for the transferred electrons.
•
The reduction of an acceptor causes the oxidation of a donor, so acceptors are called oxidizing agents or oxidants.
•
The oxidation of the donor causes the reduction of an acceptor, so donors are called reducing agents or reductants.
•
Reductants lose electrons to become oxidants, and oxidants gain electrons to become reductants.
•
A reducing agent and the oxidizing agent that it becomes when it is oxidized form a redox couple, which we will represent with the reduced form of the couple (RED) followed by a diagonal line then the oxidized form (OX) as in Cu/Cu²⁺.

9.1-2. Proton and Electron Transfer Compared

There are many similarities between Brønsted acid-base reactions and electron transfer reactions. In acid-base reactions, protons (positive charges) are transferred from a proton donor (acid) to a proton acceptor (base), while in redox reactions, electrons (negative charges) are transferred from an electron donor to an electron acceptor. In an acid-base reaction, the reacting acid and the produced base are called a conjugate acid-base pair, and in a redox reaction, the reacting donor and produced acceptor are called a redox couple. Acid-base reactions are extensive when the reacting acid and base are stronger than the produced acid and base, and redox reactions are extensive when the reacting oxidizing and reducing agents are stronger than the produced oxidizing and reducing agents.

9.1-3. The Electron Transfer Process

Figure 9.1 represents the electron transfer from an isolated iron atom to an isolated copper(II) ion to produce an iron(II) ion and a copper atom. The electrons are on Fe initially, so it is the donor (reducing agent or reductant). The produced Fe²⁺ has empty redox orbitals, so it can function as an acceptor (oxidizing agent or oxidant). Thus, Fe is a donor, and Fe²⁺ is the produced acceptor, so Fe/Fe²⁺ is one redox couple in the reaction. The acceptor orbitals on Cu²⁺ are empty, but they are occupied in Cu. Thus, Cu²⁺ is the initial acceptor and Cu is the produced donor, so Cu/Cu²⁺ is the other redox couple in the reaction. The electrons are at higher energy on the donor (Fe) than on the acceptor (Cu), so the electron transfer is downhill in energy, exothermic, and spontaneous. The electron transfer from Cu to Fe²⁺ is uphill in energy, endothermic, and NOT spontaneous.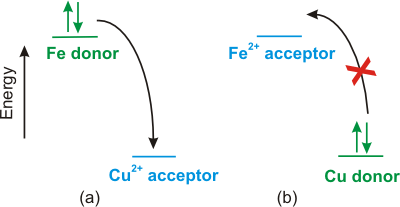

Figure 9.1: Electrons Transfer Spontaneously to Lower Energy

9.1-4. Process in Solution

We have considered electron transfer between isolated atoms and ions because the picture is far more complicated when metals and solutions are involved. Consider all that must occur when a piece of iron reacts with copper(II) ions in aqueous solution. Metallic bonds must be broken in the iron to produce an iron atom, the iron atom must lose two electrons to form Fe²⁺, a cavity must be created in the water to accommodate the ion, and the Fe²⁺ ion must enter the cavity and be hydrated. Similar processes must occur in the reverse direction when the Cu²⁺ ion is reduced to copper metal. Thus, the situation in aqueous redox reactions is far more complicated. If the energy difference between the donor and acceptor orbitals is not large, then these other factors can dominate the energy of the redox process. Consequently, the simple tendency of electrons to move from an orbital at high-energy into one at lower energy is not sufficient if the orbital energies are not very different. As in all processes carried out at constant temperature and pressure, it is the free energy change, ΔG, that is the driving force behind redox reactions.

9.1-5. Galvanic Cell Review

When steel wool (Fe) is placed into a solution of Cu²⁺, the electron transfer takes place sponteneously, and the energy released simply warms the solution. However, that energy can be harnessed by separating the two redox couples and connecting them into an electrical circuit. Such circuits are called galvanic cells, and the video below shows all of the processes that occur in a galvanic cell constructed with a Cu/Cu²⁺ couple as the cathode and a Fe/Fe²⁺ couple as the anode. By definition:

•
The cathode is the compartment where reduction takes place, so it houses the Cu/Cu²⁺ couple.
•
The anode is the compartment where oxidation takes place, so it houses the Fe/Fe²⁺ couple.

Click the "Cathode" or "Anode" button in the video to view the process that occurs in that compartment. You should note the following points:

•
Electron movement is anode → cathode.
•
The CuSO₄ solution loses its color as Cu²⁺ ions are consumed and the Cu electrode gets larger as Cu atoms are produced.
•
The Fe electrode gets smaller as iron atoms are converted into Fe²⁺ ions that pass into solution.
•
One K¹⁺ ion enters the cathode for each electron that enters to maintain electrical neutrality.
•
One Cl^1– ion enters the anode for each electron that leaves to maintain electrical neutrality.

The electrical circuit has three components:

1
charges (ions) migrate through the solution
2
electrons pass between the solution and the circuit at the surface of the electrodes, and
3
electrons move from the anode to the cathode in the external circuit.

Figure 9.2: Galvanic Cell

9.1-6. Cell Potential

The anode and cathode are each one-half of the redox process and are referred to as half-cells, and the cell potential is the potential difference between the two half-cells

( 9.1 )

ℰ = ℰ_cathode − ℰ_anode

The Cell Potential is the Difference Between the Half-cell potentials

ℰ_cathode and ℰ_anode are known as the half-cell potentials. In a redox reaction, electrons must flow from the anode (donor) to the cathode (acceptor), but electrons are also negatively charged, so they also seek the more positive electical potential (charge). Thus, electrons transfer spontaneously to the cathode if it is at the higher electrical potential, but they must be forced to transfer if the cathode is at the lower electrical potential. A galvanic cell is a cell in which ℰ_cathode > ℰ_anode (ℰ > 0), so redox reactions in galvanic cells are spontaneous (ΔG < 0). The released free energy in a galvanic cell can be used to do work. Thus, we can conclude the following.

Galvanic cells convert chemical potential energy into electrical potential energy.

All batteries are galvanic cells. The cell potential of the electrochemical cell shown in Figure 9.2 is +0.78 V, so it is a galvanic cell, and the electron transfer from Fe to Cu²⁺ is spontaneous.

9.1-7. Electrolytic Cell

An electrolytic cell is a cell in which ℰ_cathode < ℰ_anode, so ℰ < 0, and ΔG > 0. Consequently, the redox electrons must be forced to move to the more negative potential with an external power supply, so we can conclude the following.

An electrolytic cell converts electrical potential energy into chemical potential energy.

Recharging a battery and producing hydrogen and oxygen from water are two examples of the utility of electrolytic cells.

9.1-8. Standard Reduction Potentials

The criterion for spontaneous electron transfer is ℰ_cathode > ℰ_anode. Therefore, tables of half-cell potentials can be used to predict spontaneity in electron transfer reactions. However, the potential of only half of a cell cannot be measured as both a donor and an acceptor are required, so absolute half-cell potentials cannot be determined. To solve this problem, chemists chose the standard hydrogen electrode or SHE as the reference half-cell. The half-cell potential of the SHE is assigned a value of exactly zero. A SHE is represented as:

2 H¹⁺(aq) + 2 e¹⁻ ⇌ H₂(g) ℰ° = 0 V

By convention, the cell potential is measured by connecting the 'lo' or (–) lead of the voltmeter to the SHE. This convention assumes that the SHE is the oxidation and the half-cell being measured is the reduction, so the potential of the cell at standard conditions is known as the standard reduction potential of the half-reaction connected to the SHE. Consider that, if the anode of the cell shown in Figure 9.2 had been a SHE instead of an Fe/Fe²⁺ half-cell, the cell potential would have been +0.34 V, which is the standard reduction potential of the Cu/Cu²⁺ couple. The positive sign implies that the electrical potential of the Cu/Cu²⁺ couple is 0.34 V higher than that of the SHE. A more positive electrical potential means that the redox orbitals of the Cu/Cu²⁺ couple are lower in energy. If the Fe/Fe²⁺ half-cell is attached to the 'hi' (+) side and the SHE to the 'lo' (–) side, the potential would be –0.44 V, which is the standard reduction potential of the Fe/Fe²⁺ couple. The negative sign indicates that the Fe/Fe²⁺ couple is at a more negative electrical potential than the SHE, so its orbital energy is higher.

9.1-9. Oxidizing Power and Reduction Potentials

The standard reduction potential of a redox couple is a measure of the electrical potential of the electron in the couple. Therefore, the standard cell potential can be determined from tabulated standard reduction potentials by rewriting Equation 9.1

ℰ = ℰ_cathode − ℰ_anode

for standard conditions.

ℰ° = ℰ°_cathode − ℰ°_anode

ℰ°_cathode is the standard reduction potential of the redox couple in the cathode and ℰ°_anode is the standard reduction potential of the redox couple in the anode. For example, consider the reaction between Cu²⁺ and Fe in Figure 9.2.
ℰ°_cathode = +0.34 V (the standard reduction potential of the Cu/Cu²⁺ couple) and ℰ°_anode = –0.44 V (the standard reduction potential of the Fe/Fe²⁺ couple). Using Equation 9.1

ℰ = ℰ_cathode − ℰ_anode

, we determine that ℰ° = +0.34 – (–0.44) = +0.78 V. ℰ° is positive (the reaction is extensive) when ℰ°_cathode is high and ℰ°_anode is low or negative. Therefore, we can conclude the following.

Good oxidizing agents have high standard reduction potentials and good reducing agents have low or negative standard reduction potentials.

9.2 Balancing Redox Reactions

Introduction

Redox reactions can be difficult to balance because the loss and gain of redox electrons must also be balanced, but there are two methods that simplify the task: the half-reaction method, which is readily applied to ionic equations; and the oxidation state change method, which is useful when balancing reactions that do not involve ions. Balancing redox reactions with these methods is something chemists do occasionally, but not frequently, so these tools are not presented here. All balanced redox reactions in this chapter are constructed from tabulated half-reactions.

Prerequisites

•
CAMS 11.1 Electron Transfer or Redox Reactions (Explain the redox process and the common terms used to describe it.)
•
CAMS 11.2 Half-Reactions (Write a balanced redox reaction given a table of reduction half-reactions.)
•
CAMS 11.3 Galvanic Cells (Explain the workings of a galvanic cell.)
•
CAMS 11.4 Standard Reduction Potentials (Explain what standard reduction potentials are and how they are used.)
•
CAMS 11.5 Writing Redox Reactions (Use a table of standard reduction potentials to predict whether a redox reaction takes place when two substances are mixed.)

9.2-1. Method

Redox reactions are frequently balanced by using tabulated half-reactions like those given in the Resource titled Selected Standard Reduction Potentials at 298 K. To write the spontaneous reaction from two reduction half reactions:

1
Determine which half reaction has the less positive or more negative reduction potential and reverse it as it must serve as the oxidation half-reaction (anode).
2
Determine the number of electrons transferred in the balanced chemical equation. This is the lowest common multiple (LCM) of the number gained at the cathode and the number lost at the anode.
3
Multiply each half-reaction through by the integer required to make the number of electrons gained or lost in the half-reaction equal to the LCM determined in Step 2.
4
Add the resulting half-reactions to obtain the cell reaction. Note that the same substance cannot appear on both sides of the equation, so H₂O, H¹⁺, and OH^1– can often be canceled and not appear in the net equation.
5
Determine the cell potential as ℰ°_cell = ℰ°_cathode – ℰ°_anode.

9.2-2. Half-cell Potentials and Balancing Equations

A standard reduction potential is a measure of the electrical potential or free energy of a redox electron, so it is independent of the number of electrons or the side of the half-reaction on which they are found. We conclude the following important fact.

The standard reduction potential of a half-reaction is not changed when the direction of the half-reaction is reversed or when it is is multiplied by an integer.

In other words, the fact that standard reduction potential for the Cu/Cu²⁺ couple is +0.34 V simply means that the electrical potential experienced by an electron in the Cu/Cu²⁺ couple is 0.34 V higher than that experienced by one in the H₂/H¹⁺ couple. That fact is true whether the Cu is a reactant or a product or whether there are one, two, or three Cu atoms.

9.2-3. Exercise

Exercise 9.1:

Write the balanced chemical equation for the spontaneous process that involves the following half reactions and determine the standard cell potential.

VO₂¹⁺ + 2 H¹⁺ + e^1– ⇌ VO²⁺ + H₂O ℰ° = +1.00 V
Cr₂O₇^2– + 14 H¹⁺ + 6 e^1– ⇌ 2 Cr³⁺ + 7 H₂O ℰ° = +1.33 V

1) Identify the reaction that must be reversed and serves as the anode.

VO₂¹⁺ + 2 H¹⁺ + e^1– ⇌ VO²⁺ + H₂O
Cr₂O₇^2– + 14 H¹⁺ + 6 e^1– ⇌ 2 Cr³⁺ + 7 H₂O The oxidation half reaction of a spontaneous cell must be the half reaction with the smaller (more negative) standard half-cell potential.

2) Determine the number of electrons that must be transferred in the reaction.

n = 6_0__0 One electron is lost in the oxidation and six are gained in the reduction. n is the LCM of 1 and 6.

Indicate any subscripted characters with an underscore (_) and any superscipted characters with a caret (^). For example, NH_4^1+ for NH₄¹⁺. Include any coefficients other than 1. Omit any spaces.

3a) Determine the anode half reaction as it occurs in the overall reaction (after reversing and multiplying by the appropriate integer).

o_6VO^2+_s 6VO²⁺ + 6H₂O ⇌ 6VO₂¹⁺ + 12H¹⁺ + 6e^1–

o_6H_2O_s 6VO²⁺ + 6H₂O ⇌ 6VO₂¹⁺ + 12H¹⁺ + 6e^1–

→

o_6VO_2^1+_s 6VO²⁺ + 6H₂O ⇌ 6VO₂¹⁺ + 12H¹⁺ + 6e^1–

o_12H^1+_s 6VO²⁺ + 6H₂O ⇌ 6VO₂¹⁺ + 12H¹⁺ + 6e^1–

6_0__ 6VO²⁺ + 6H₂O ⇌ 6VO₂¹⁺ + 12H¹⁺ + 6e^1– e^1–

3b) Determine the cathode half reaction as it occurs in the overall reaction (after multiplying by the appropriate integer).

o_Cr_2O_7^2-_s Cr₂O₇^2– + 14H¹⁺ + 6e^1– ⇌ 2Cr³⁺ + 7H₂O

o_14H^1+_s Cr₂O₇^2– + 14H¹⁺ + 6e^1– ⇌ 2Cr³⁺ + 7H₂O

6_0__ Cr₂O₇^2– + 14 H¹⁺ + 6 e^1– ⇌ 2 Cr³⁺ + 7 H₂O e^1–

→

o_2Cr^3+_s Cr₂O₇^2– + 14H¹⁺ + 6e^1– ⇌ 2Cr³⁺ + 7H₂O

o_7H_2O_s Cr₂O₇^2– + 14H¹⁺ + 6e^1– ⇌ 2Cr³⁺ + 7H₂O

4) Write the chemical equation (Red₁ + Ox₂ + Other → Ox₁ + Red₂ + Other) for the spontaneous process.

o_6VO^2+_s 6VO²⁺ + Cr₂O₇^2- + 2H¹⁺ ⇌ 6VO₂¹⁺ + 2Cr³⁺ + H₂O

o_Cr_2O_7^2-_s 6VO²⁺ + Cr₂O₇^2- + 2H¹⁺ ⇌ 6VO₂¹⁺ + 2Cr³⁺ + H₂O

o_2H^1+_s 6VO²⁺ + Cr₂O₇^2- + 2H¹⁺ ⇌ 6VO₂¹⁺ + 2Cr³⁺ + H₂O

→

o_6VO_2^1+_s 6VO²⁺ + Cr₂O₇^2- + 2H¹⁺ ⇌ 6VO₂¹⁺ + 2Cr³⁺ + H₂O

o_2Cr^3+_s 6VO²⁺ + Cr₂O₇^2- + 2H¹⁺ ⇌ 6VO₂¹⁺ + 2Cr³⁺ + H₂O

o_H_2O_s 6VO²⁺ + Cr₂O₇^2- + 2H¹⁺ ⇌ 6VO₂¹⁺ + 2Cr³⁺ + H₂O

5) What is the standard cell potential?

ℰ° = 0.33_0__ Use Equation 9.1:ℰ° = 1.33 – 1.00 V

9.2-4. Exercise

Exercise 9.2:

Given the following half-reactions,

Au³⁺ + 3 e^1– ⇌ Au
MnO₄^1– + 8 H¹⁺ + 5 e^1– ⇌ Mn²⁺ + 4 H₂O

write the overall reaction for the oxidation of gold by permanganate ion.

1) The lowest common multiple of electrons gained and lost is:

n = 15_0__ the LCM of 3 and 5 is 15

2) Which half reaction must be reversed to an oxidation?

Au³⁺ + 3 e^1– ⇌ Au
MnO₄^1– + 8 H¹⁺ + 5 e^1– ⇌ Mn²⁺ + 4 H₂O The problem specifies the oxidation of gold.

3) The anode half reaction as it occurs in the overall reaction (after reversing and multiplying by the appropriate integer):

o_5Au_s Multiply reaction by 5 to get 15 electrons and reverse it to make it the oxidation: 5Au → 5Au³⁺ + 15e^1–

→

o_5Au^3+_s Multiply reaction by 5 to get 15 electrons and reverse it to make it the oxidation: 5Au → 5Au³⁺ + 15e^1–

15_0__ Multiply reaction by 5 to get 15 electrons and reverse it to make it the oxidation: 5Au → 5Au³⁺ + 15e^1– e^1–

4) The cathode half reaction as it occurs in the overall reaction (after multiplying by the appropriate integer):

o_3MnO_4^1-_s Multiply by 3 to get 15 electrons: 3MnO₄^1– + 24H¹⁺ + 15e^1– → 3Mn²⁺ + 12H₂O

o_24H^1+_s Multiply by 3 to get 15 electrons: 3MnO₄^1– + 24H¹⁺ + 15e^1– → 3Mn²⁺ + 12H₂O

15_0__ Multiply by 3 to get 15 electrons: 3MnO₄^1– + 24H¹⁺ + 15e^1– → 3Mn²⁺ + 12H₂O e^1–

→

o_3Mn^2+_s Multiply by 3 to get 15 electrons: 3MnO₄^1– + 24H¹⁺ + 15e^1– → 3Mn²⁺ + 12H₂O

o_12H_2O_s Multiply by 3 to get 15 electrons: 3MnO₄^1– + 24H¹⁺ + 15e^1– → 3Mn²⁺ + 12H₂O

5) Write the chemical equation (Red₁ + Ox₂ + Other → Ox₁ + Red₂ + Other) for the spontaneous process.

o_5Au_s 5Au + 3MnO₄^1– + 24H¹⁺ → 5Au³⁺ + 3Mn²⁺ + 12H₂O

o_3MnO_4^1-_s 5Au + 3MnO₄^1– + 24H¹⁺ → 5Au³⁺ + 3Mn²⁺ + 12H₂O

o_24H^1+_s 5Au + 3MnO₄^1– + 24H¹⁺ → 5Au³⁺ + 3Mn²⁺ + 12H₂O

→

o_5Au^3+_s 5Au + 3MnO₄^1– + 24H¹⁺ → 5Au³⁺ + 3Mn²⁺ + 12H₂O

o_3Mn^2+_s 5Au + 3MnO₄^1– + 24H¹⁺ → 5Au³⁺ + 3Mn²⁺ + 12H₂O

o_12H_2O_s 5Au + 3MnO₄^1– + 24H¹⁺ → 5Au³⁺ + 3Mn²⁺ + 12H₂O

9.3 Free Energy and Electrochemical Cells

Introduction

We now continue our treatment of galvanic cells and begin our discussion of their thermodynamics.

Objectives

•
Determine the anode and cathode reactions of the spontaneous cell given the standard reduction potentials of the two half-reactions.
•
Express an electrochemical cell in the abbreviated form.
•
Determine the free energy of a redox reaction from its cell potential, and vice versa.

9.3-1. Electrodes

Electron transfer reactions in electrochemical cells are known as electrochemical reactions. Electrochemical reactions occur at the surfaces of the two electrodes in the cell as electrons are injected into the external circuit at the anode as the donor is oxidized and withdrawn from the circuit at the cathode as the acceptor is reduced. Electrodes that take part in the electrochemical reactions are said to be active electrodes. For example, the iron and copper electrodes in the galvanic cell discussed in the previous section are active electrodes because both are involved in the reaction. However, there are many instances where neither member of a redox couple is a conducting solid, but an electrode is still required to serve as the interface between the reaction and the circuit. In these cases, an inert metal is normally used as a passive electrode. Passive electrodes do not participate in the reaction; they simply serve as a conducting surface through which electrons are injected into either the circuit or the reaction. For example, a Pt electrode is commonly used in a Standard Hydrogen Electrode (SHE) because there is no metal surface in the half-reaction (2 H¹⁺ + 2 e^1– ⇌ H₂).

9.3-2. Electrochemical Cell Abbreviation

Electrochemical cells are quite common and are often represented in the following abbreviated form:

anode electrode | anode compartment || cathode compartment | cathode electrode

A single vertical line represents a phase change (solid/solution), and a double vertical line represents a liquid junction (salt bridge). The order in which components are listed is easily remembered if you remember your ABC's (Anode | Bridge | Cathode). As an example, the cell shown in Figure 9.2 is represented as

Fe | Fe²⁺(1 M) || Cu²⁺(1 M) | Cu

and the cell in which the SHE is the anode and copper is the cathode is

Pt | H₂(1 atm), H¹⁺(1 M) || Cu²⁺(1 M) | Cu

where a platinum wire serves as a passive electrode for the standard hydrogen electrode. Note that the order of components in a half-cell with a passive electrode is not specified, so the order in which H₂ and H¹⁺ appear in the anode is not fixed.

9.3-3. Cell Abbreviation Exercise

Exercise 9.3:

Write the chemical equation for the following redox process:

Al | Al³⁺(1 M) || Sn²⁺(1 M) | Sn

Lowest common multiple for electrons gained and lost.

n = 6_0__ LCM of 2 and 3

Write the chemical equation (Red₁ + Ox₂ → Ox₁ + Red₂). (Indicate any subscripted characters with an underscore (_) and any superscipted characters with a caret (^). For example, NH_4^1+ for NH₄¹⁺. Include any coefficients other than 1. Omit any spaces.)

o_2Al_s 2Al + 3Sn²⁺ → 2Al³⁺ + 3Sn

o_3Sn^2+_s 2Al + 3Sn²⁺ → 2Al³⁺ + 3Sn

→

o_2Al^3+_s 2Al + 3Sn²⁺ → 2Al³⁺ + 3Sn

o_3Sn_s 2Al + 3Sn²⁺ → 2Al³⁺ + 3Sn

The standard reduction potentials of Al and Sn are –1.66 V and –0.14 V, respectively. What is the cell potential?

ℰ° = 1.52_0__ Use Equation 9.1. ℰ_cathode = –0.14 V and ℰ_anode = –1.66 V. V

9.3-4. Free Energy

Recall from Equation 4.9 that the maximum amount of work that can be obtained from a process is the amount of free energy released during the process. Thus, the amount of work that can be done by the transferred electrons in a spontaneous redox reaction is:

( 9.2 )

work done by electrons = −ΔG

Work Done by the Electrons in terms of Free Energy Change

Historically, the work done by the transferred electrons was expressed in terms of charge and electrical potential difference, ℰ. The absolute value of the charge of one mole of electrons is called the faraday and given the symbol ℱ. The faraday is Avogadro's number times the absolute value of the charge on a single electron:

ℱ = 6.02214 × 10²³ electrons/mol × 1.60218 × 10⁻¹⁹ C/electron = 9.6485 × 10⁴ C/mol

Equation 9.3 expresses the work that can be done by the transfer of n moles of electrons through an electrical potential ℰ.

( 9.3 )

work done by electrons = nℱℰ

Work is Charge times Electrical Potential

Equating the two expressions for the work done by the electrons in a redox reaction, we obtain the expressions for the free energy in terms of the cell potential given in Equation 9.4.

( 9.4 )

ΔG = −nℱℰ

Free Energy and Cell Potential

Of course superscript zeros can be added to the above for the electron transfer under standard conditions.

9.3-5. Free Energy from Cell Potential Exercise

Exercise 9.4:

Use Equation 9.4

ΔG = −nℱℰ

to determine the standard free energy change for the following reaction:

3 Sn²⁺ + 2 Al → 2 Al³⁺ + 3 Sn ℰ° = 1.52 V

ΔG° = -880_0_3_ Use Equation 9.4, n = 6, and convert to kJ.ΔG° = –(6 mol e^1–)(96,500 C/mol e^1–)(1.52 J/C) = –8.80 e05 J = –880. kJ kJ

9.4 The Effect of Concentration on Cell Potential

Introduction

The cell potential is a measure of the chemical free energy of a redox reaction, and we now apply the relationships between the reaction quotient, the equilibrium constant, and the free energy of reaction presented in Chapter 4 to electrochemical processes. These relationships allow us to derive an expression for the effect of concentration on cell potential.

Objectives

•
Determine the cell potential of a redox reaction given the standard cell potential and the concentrations of all reactants and products.

9.4-1. Nernst Equation

To determine the effect of concentrations on cell potentials, we start with Equation 4.13:

ΔG = ΔG° + RT ln Q

Then use ΔG = –nℱℰ to obtain the following:

−nℱℰ = −nℱℰ° + RT ln Q

Next, divide both sides by –nℱ to obtain an expression for the cell potential in terms of the standard cell potential and the reaction quotient.

ℰ = ℰ° −

nℱ

ln Q

Finally, use ln Q = 2.303 log Q to convert to log base 10 and assume that T = 298 K to obtain the Nernst equation.

( 9.5 )

ℰ = ℰ° −

0.0592

log Q

Nernst Equation at 25 °C

The Nernst equation allows us to determine the cell potential at 25 °C from the standard cell potential and the concentrations of the reactants and products (Q).

9.4-2. Determine Potential After Cell Discharge Exercise

Exercise 9.5:

Consider the following cell:

Al | Al³⁺ (1.00 M) || Sn²⁺ (1.00 M) | Sn ℰ° = 1.52 V

What is the cell potential if the cell is discharged from standard conditions to the point where [Sn²⁺] = 0.01 M? Assume that the volumes of the two half-cells are the same when determining Δ.

First, fill in the reaction table to determine the final concentration of Al³⁺.

2 Al

3 Sn²⁺

→

2 Al³⁺

3 Sn

initial

1.00_0_3_ The cell is at standard conditions initially, so all concentrations are 1.00 M.

-0.99_0__ The initial and final concentrations are given as 1.00 M and 0.01 M, respectively. Δ = final – initial = 0.01 – 1.00 = –0.99 M.

+0.66_0__ The Δ line entry for Sn²⁺ is known, so this entry can be determined by stoichiometry.

0.99 mol Sn²⁺ react

2 mol Al³⁺ form

3 mol Sn²⁺ react

= 0.66 mol Al³⁺ form

final

0.01_0__ This value is given.

1.66_0__ 1.00 M initially + 0.66 M form = 1.66 M

The value of Q = 3e6_0__

Q =

[Al³⁺]²

[Sn²⁺]³

(1.66)²

(0.01)³

= 3e6

Use Equation 9.5

ℰ = ℰ° −

0.0592

log Q

to determine the cell potential.

ℰ = 1.46_0__ Substitute into Equation 9.5.

ℰ = 1.52 −

0.0592

log(3e6) = 1.46 V

9.4-3. Cell Thermodynamics Exercise

Exercise 9.6:

Consider the following cell at 25 °C.

Pb | Pb²⁺ (0.12 M) || Cu¹⁺ (0.020 M) | Cu ℰ = 0.58 V

Write the chemical equation for the cell reaction (Red₁ + Ox₂ → Ox₁ + Red₂). (Indicate any subscripted characters with an underscore (_) and any superscipted characters with a caret (^). For example, NH_4^1+ for NH₄¹⁺. Include any coefficients other than 1. Omit any spaces.)

o_Pb_s Pb + 2Cu¹⁺ → Pb²⁺ + 2Cu

o_2Cu^1+_s Pb + 2Cu¹⁺ → Pb²⁺ + 2Cu

→

o_Pb^2+_s Pb + 2Cu¹⁺ → Pb²⁺ + 2Cu

o_2Cu_s Pb + 2Cu¹⁺ → Pb²⁺ + 2Cu

n = 2_0__ Pb → Pb²⁺ involves the loss of how many electrons. electrons transferred

ΔG = -110_0_2_ ΔG = –nℱℰ = –(2 mol)(96,500 C/mol)(0.58 J/C)(1 kJ/1000 J) kJ

Q = 300_0_2_

Q =

[Pb²⁺]

[Cu¹⁺]²

0.12

(0.020)²

= 3.0e2

ℰ° = 0.65_0__ Solve Equation 9.5 for ℰ° and substitute the known values

ℰ° = ℰ +

0.0592

log Q = 0.58 +

0.0592

log(300)

ΔG° = -130_0_2_ Use Equation 9.4: ΔG° = –(2 mol)(96,500 C/mol)(0.65 J/C)(1 kJ/1000 J) = –125 kJ However, the answer is good to only two significant figures, -130 kJ. kJ

Given that the standard reduction potential of Pb²⁺ is –0.13 V, determine the standard reduction potential of Cu¹⁺.

ℰ° = 0.52_0__ The Cu¹⁺/Cu couple is in the cathode, so solve Equation 9.1 for ℰ°_cathode = ℰ° + ℰ°_anodeSubstitute the known values: ℰ°_cathode = 0.65 + (–0.13) = 0.52 V. V

9.4-4. pH from Cell Potential Exercise

Exercise 9.7:

A pH meter is an electrochemical cell whose voltage is pH dependent. This example shows how a pH meter could be constructed from a SHE and an Ag/AgCl couple. Of course, the SHE is far too cumbersome to be used in a real pH meter, but the principle is the same.

Determine the pH of the solution in the anode compartment of the following cell if the cell potential is 0.53 V.

Pt | H₂ (1.00 atm), H¹⁺ (x M) || Cl^1– (1.00 M), AgCl | Ag

Determine the half-reactions, their standard reduction potentials, the chemical equation for the overall reaction (Red₁ + Ox₂ → Ox₁ + Red₂ + Other), and its standard cell potential. Write the half-reactions so that the electrons cancel in the sum. (Selected Standard Reduction Potentials at 298 K. Indicate any subscripted characters with an underscore (_) and any superscipted characters with a caret (^). For example, NH_4^1+ for NH₄¹⁺. Include any coefficients other than 1. Omit any spaces.)

	Reaction									ℰ°
Anode	o_H_2_s H₂/H¹⁺ couple is in the anode, so it must be written as the oxidation. Pt is a passive electrode. Anode: H₂ → 2 H¹⁺ + 2 e^1–	→	o_2H^1+_s H₂/H¹⁺ couple is in the anode, so it must be written as the oxidation. Pt is a passive electrode. Anode: H₂ → 2 H¹⁺ + 2 e^1–	+	2_0__ H₂/H¹⁺ couple is in the anode, so it must be written as the oxidation. Pt is a passive electrode. Anode: H₂ → 2 H¹⁺ + 2 e^1– e^1–					0___ The tabulated value is 0.00 V. V
Cathode	o_2AgCl_s Ag/AgCl is in the cathode, so it must be written as the reduction. Ag is an active electrode. This is a two-electron transfer, so cathode: 2AgCl + 2e^1– → 2Ag + 2Cl^1–	+	2_0__ Ag/AgCl is in the cathode, so it must be written as the reduction. Ag is an active electrode. This is a two-electron transfer, so cathode: 2AgCl + 2e^1– → 2Ag + 2Cl^1– e^1–	→	o_2Ag_s Ag/AgCl is in the cathode, so it must be written as the reduction. Ag is an active electrode. This is a two-electron transfer, so cathode: 2AgCl + 2e^1– → 2Ag + 2Cl^1–	+	o_2Cl^1-_s Ag/AgCl is in the cathode, so it must be written as the reduction. Ag is an active electrode. This is a two-electron transfer, so cathode: 2AgCl + 2e^1– → 2Ag + 2Cl^1–			0.22_0__ The tabulated value is +0.22 V. V
Cell	o_H_2_s Sum the two half-reactions to obtain: H₂ + 2AgCl → 2H¹⁺ + 2Ag + 2Cl^1–	+	o_2AgCl_s Sum the two half-reactions to obtain: H₂ + 2AgCl → 2H¹⁺ + 2Ag + 2Cl^1–	→	o_2H^1+_s Sum the two half-reactions to obtain: H₂ + 2AgCl → 2H¹⁺ + 2Ag + 2Cl^1–	+	o_2Ag_s Sum the two half-reactions to obtain: H₂ + 2AgCl → 2H¹⁺ + 2Ag + 2Cl^1–	+	o_2Cl^1-_s Sum the two half-reactions to obtain: H₂ + 2AgCl → 2H¹⁺ + 2Ag + 2Cl^1–	0.22_0__ Use Equation 9.1 and ℰ°_cathode = +0.22 V. V

n = 2_0__ H₂ → 2 H¹⁺ requires the loss of how many electrons? electrons transferred

log Q = -11_0_2_

log Q =

0.0592

(ℰ° − ℰ) =

0.0592

(0.22 − 0.53) = −10.5 = −11

pH = 5.2_0_2_

log Q = log

[Cl¹]²[H¹⁺]²

P_H₂

= log

(1.0)²[H¹⁺]²

1.0

= log [H¹⁺]²

log [H¹⁺]² = 2 log [H¹⁺] = –2 pH,
pH = –(log Q)/2 = –(–10.5)/2 = 5.2 (Note: log [H¹⁺]² = –2 pH)

9.4-5. Qualitative Change in Cell Potential

indicates that ℰ increases as log Q decreases, so any change that decreases Q (decreasing a product concentration or increasing a reactant concentration) increases the cell potential. Similarly, any change that increases Q (increasing a product concentration or decreasing a reactant concentration) decreases the cell potential. This is the same direction that LeChâtelier's principle predicts for a product.

Cell potential is a product of a spontaneous redox reaction, so any change in the reaction that causes the equilibrium amount of product to increase will increase the cell potential, and any change that causes the amount of product to decrease will reduce the cell potential.

9.4-6. Effect of Changing Conditions on Cell Potential Exercise

9.4-7. Changing Conditions Exercise

9.4-8. Equilibrium Constants and Standard Cell Potentials

At equilibrium, Q = K and ΔG = 0. However, ΔG = –nℱℰ, so ℰ = 0 as well. Thus, batteries die when the reaction reaches equilibrium. Applying these equilibrium conditions to Equation 9.5

ℰ = ℰ° −

0.0592

log Q

, we obtain the following:

0 = ℰ° −

0.0592

log K

Solving the above for ℰ°, we get Equation 9.6.

( 9.6 )

ℰ° =

0.0592

log K

Standard Cell Potential in Terms of log K

Alternatively, we can solve for log K to get Equation 9.7.

( 9.7 )

log K =

nℰ°

0.0592

= 16.9nℰ°

Log K in Terms of the Standard Cell Potential

Equation 9.7 indicates that log K increases as ℰ° increases. Thus, the extent of a redox reaction increases as its standard cell potential increases. The extent of a redox reaction is often referred to as the extent of electron transfer.

9.4-9. Determining K from Standard Cell Potential Exercise

Exercise 9.10:

What is the equilibrium constant for the following reaction?

3 Sn²⁺ + 2 Al → 3 Sn + 2 Al³⁺ ℰ° = 1.52 V

n = 6_0__ n = 6

log K = 154_0__ Use Equation 9.7. log K = 16.9nℰ° = (16.9)(6)(1.52) = 154

K = 1e154___ K = 10^{log K} = 1 e154 (1x10¹⁵⁴)

9.5 The Electrolytic Cell

Introduction

A second technological side of electrochemistry is based on the use of external electrical circuits to control the redox chemistry itself, including the ability to force electrons uphill in energy. The process of forcing electrons uphill in energy is called electrolysis. An electrolysis reaction is one that converts electrical potential energy into chemical potential energy. Recharging batteries, electroplating, recovering elemental metals from ores, and making chemicals are some examples of electrolysis. The electrochemical cell that is used to do an electrolysis experiment is called an electrolytic cell.

Prerequisites

•
CAMS 11.8 Electrolytic Cells (Distinguish between electrolytic and galvanic cells.)
•
CAMS 8.6 Fermi Level (Define a metallic band and the Fermi level.)

Objectives

•
Describe how an electrolytic cell works.
•
Determine the minimum voltage that must be applied in an electrolytic cell.

9.5-1. Electrodes

The voltage across two electrodes measures the energy difference in their Fermi levels.

Consider the figure of a power supply connected to two pieces of metal. The power supply removes electrons from the metal attached to the positive terminal and adds electrons to the metal attached to the negative terminal. The electrons added to one side occupy orbitals in the band of the metal and thus raise the Fermi level of that metal. The electrons that are removed from the other metal come from orbitals in the metallic band, so the Fermi level of that metal is lowered. The potential difference between the two pieces of metal that is caused by the power supply is the energy difference between the two Fermi levels.

Figure 9.3: Applied Potential and Electrode Fermi Levels

The orange rectangles represent the conduction band occupancies of two pieces of the same metal. (a) When no potential is applied to the metals, their band populations and therefore their Fermi levels are the same; i.e., there is no potential difference. (b) Application of an electrical potential causes the Fermi level of the anode to drop as electrons are removed and the Fermi level of the cathode to increase as electrons are added. The potential difference in the Fermi levels equals the applied potential

Recall that the cathode is the electrode where reduction takes place, so it is the electrode toward which the electrons move. In a galvanic cell they move spontaneously toward the positive electrode, which is the cathode. However, the power supply pushes the electrons toward the negative electrode in an electrolytic cell, so the negative electrode is the cathode and the reduction half reaction takes place there. Similarly, the positive electrode in an electrolytic cell is the anode, which is where oxidation takes place. Thus, the signs of the electrodes in an electrolytic cell are opposite what they are in a galvanic cell.

9.5-2. Ion Migration

Anions migrate toward electrodes at positive potential (anode), while cations migrate toward the electrode at negative potential (cathode).

Molten salts and aqueous solutions of electrolytes conduct electricity when a sufficient voltage is applied across two electrodes immersed in them because the ions (electrolytes) are mobile and migrate toward the electrodes. Cations move toward the cathode because it is at a negative potential, and anions move toward the anode because it is at a positive potential. Thus, the cathode is surrounded by cations, while the anode is surrounded by anions. Indeed, the names 'cation' and 'anion' derive from this behavior: anions move toward the anode and cations move toward the cathode.

Figure 9.4: Ions move toward electrodes Click 'Apply Voltage' to see the effect of an applied voltage on the ions between the electrodes.

9.5-3. Potential Required for the Electrolysis of NaCl

When the cell potential is great enough, electrons can be forced from the cathode to the surrounding cations and to the anode from the surrounding anions. The resulting electron transfer reactions combine to produce a process called electrolysis. In an electrolysis experiment, which is carried out in an electrolytic cell, electrical potential is converted into chemical potential because the produced species are at a greater free energy than the reacting ones. We examine their function by studying the electrolysis of NaCl.

2 NaCl → 2 Na + Cl₂ ΔG°₂₉₈ = +768 kJ

The reaction is not spontaneous at standard conditions and 298 K, but it can be made to occur by an input of energy sufficient to overcome the positive ΔG°. This energy can be supplied by a power supply in an electrolytic cell. We can estimate the cell voltage required from the value of ΔG° with Equation 9.4

ΔG = −nℱℰ

as follows.

ℰ° =

ΔG°_f

nℱ

768,000 J

(2 mol)(96,500 C/mol)

= −4 V

The negative sign implies that 4 V must be applied to the cell. Alternatively, we could use the standard reduction potentials as follows.

cathode	2 Na¹⁺ + 2 e^1– → 2Na	ℰ°_cathode = –2.7 V
anode	2 Cl^1– → Cl₂ + 2 e^1–	ℰ°_anode = +1.4 V
cell	2 NaCl → 2 Na¹⁺ + 2 Cl^1–	ℰ°_cell = –2.7 – 1.4 = –4 V

Both methods assume 298 K, and the half reactions represent aqueous solution. Our discussions are concerned with the molten salt, which must be heated to about 800 °C, so the applied voltage may differ from the 4 V calculated here. However, we will use 4 V for the discussion in the next section. Our conclusion is that NaCl can be electrolyzed to Na and Cl₂ by the application of over 4 V from an external power supply.

9.5-4. Electrolysis of NaCl

When the applied voltage is such that the energy of the electrons at the Fermi level of the cathode is higher than the empty valence orbitals on the oxidant (Na¹⁺), and the energy of unfilled orbitals at the Fermi level in the anode is less than the valence electrons on the reductant (Cl^1–), electrons flow through the circuit, and electricity is conducted through the melt. Conduction in an electrolytic cell is called electrolytic conduction. Note that the direction of electron flow is from positive to negative as the power supply forces the electrons to lower (more negative) potential. Forcing electrons to move in this direction requires energy, which is stored in the higher free energy of the products. Thus,

•
An electrolytic cell converts the electrical potential energy generated in the power supply into chemical potential energy, which is stored in the sodium metal and chlorine gas.

Figure 9.5: Electrolysis of NaCl When the applied voltage is sufficient, electrons move from the reductant to the anode and from the cathode to the oxidant. A sodium ion (oxidant) that is reduced to sodium metal is replaced by another sodium ion in the melt as the positive cations continue to migrate toward the cathode. Similarly, a chloride ion that is oxidized to a chlorine atom at the anode is replaced by another chloride ion from the melt as the anions continue to migrate toward the anode.

9.5-5. Predicting the Required Voltage Exercise

Exercise 9.11:

What voltage must be applied to electrolyze water? The relevant half-reactions from Selected Standard Reduction Potentials at 298 K are:

2 H₂O + 2 e^1– ⇌ H₂ + 2 OH^1– ℰ° = –0.41 V
O₂ + 4 H¹⁺ + 4 e^1– ⇌ 2 H₂O ℰ° = +0.82 V

Use the fact that H¹⁺ + OH^1– → H₂O to write the cell reaction. (Indicate any subscripted characters with an underscore (_) and any superscipted characters with a caret (^). For example, NH_4^1+ for NH₄¹⁺. Include any coefficients other than 1. Omit any spaces.)

o_2H_2O_s This is the electrolysis of water, so water is the only reactant. It is also a four-electron reaction. Consequently, the O₂ half-reaction must be reversed and become the anode half-reaction, and the half-reaction involving only two electrons must be doubled: 2H₂O → 2H₂ + O₂

→

o_2H_2_s This is the electrolysis of water, so water is the only reactant. It is also a four-electron reaction. Consequently, the O₂ half-reaction must be reversed and become the anode half-reaction, and the half-reaction involving only two electrons must be doubled: 2 H₂O → 2 H₂ + O₂

o_O_2_s This is the electrolysis of water, so water is the only reactant. It is also a four-electron reaction. Consequently, the O₂ half-reaction must be reversed and become the anode half-reaction, and the half-reaction involving only two electrons must be doubled: 2 H₂O → 2 H₂ + O₂

Required voltage = 1.23_0__ Use Equation 9.1, ℰ_cathode = –0.41 V, and ℰ_anode = +0.82 V. ℰ = ℰ_cathode – ℰ_anode = –0.41 V – 0.82 V = –1.23 V
The minus sign simply means that the 1.23 V must be applied. V

9.5-6. Overpotential

The minimum voltage required to electrolyze water was determined to be 1.23 V in the previous exercise, but the rates of the two half-reactions are negligible at that potential because the activation energies of the two half-reactions are so high. To obtain reasonable reaction rates, the applied potential must be about 1 V higher than the predicted value.

•
The amount by which the potential must be increased above the predicted value to obtain a reasonable rate of reaction is called the overpotential.

The overpotential for each of the water half-reactions is about 0.5 volt. Overpotentials can be very difficult to predict because they depend not only upon the reaction, but also upon the electrode and the ions in solution.

9.6 Predicting the Products of Electrolysis

Introduction

The electrolysis of a mixture of several components usually produces only one product at each electrode. In this section we discuss some guidelines to use in predicting which product forms.

Objectives

•
Predict the products of the electrolysis of a mixture.

9.6-1. Predicting the Products of Electrolysis

The predominant products formed in the electrolysis of a mixture are usually those from the components of the mixture that are most easily oxidized and reduced.

•
The species that forms at the cathode is usually the reduced form of the best oxidant (most positive or least negative reduction potential).
•
The species that forms at the anode is usually the oxidized form of the best reductant (least positive or most negative reduction potential).

We use the word 'usually' in the above because the situation can be complicated by high overpotentials. In these cases, reaction of the best oxidant or reductant may be negligibly slow at the predicted potential, and weaker oxidants or reductants with smaller overpotentials may react first. Many electrolysis experiments are performed in water, and water's large overpotential can make predictions difficult. This is the case in the electrolysis of sea water, where chloride ion is oxidized to chlorine gas even though its reduction potential (+1.36 V) is more positive than that for the oxidation of water to oxygen gas (+0.88 V at pH = 7).

9.6-2. Predicting the Products Exercise

9.7 Stoichiometry of Electrochemistry

Introduction

By the 1830s, Michael Faraday had discovered that, when a chemical reaction was harnessed to an electrical current using an electrochemical cell, the amount of electricity produced or consumed corresponded directly to the amount of chemical reactant involved. In this section, we discuss these quantitative aspects of the electrochemical cell.

Objectives

•
Determine the mass of product given the amount of charge that has flowed through the cell.
•
Determine the number of coulombs of charge that are passed through a circuit given the current and the length of time the current flowed.
•
Determine the mass of product given the current and the length of time the current flowed.
•
Determine how long a given current must be applied in order to produce a given amount of product.

9.7-1. Relating the Charge Passed to the Mass formed

The electron is a reactant or a product in all half-reactions, so it is an integral part of the cell stoichiometry. However, we do not determine the mass or volume of electrons involved as we would with other reactants and products. Instead, we determine the charge in coulombs that passes during the reaction, which is measured with a coulometer. The number of coulombs that are transferred can then converted to moles of electrons with the use of the faraday, which is 96,500 C/1 mol electrons. The number of moles of electrons is converted to moles of product by using the stoichiometry of the half-reaction that involves the given species. We do the following exercises in single steps, but the answer to each step is the starting point for the following step. Thus, the steps can be combined into a single factor-label exercise. This alternate method is shown in the feedback of the final answer in each problem.

9.7-2. Charge to Mass Exercise

Exercise 9.13:

What mass of copper is produced by passing 2.00 × 10⁴ C through a solution of Cu²⁺?

First, convert the charge to moles of electrons:

0.207_0__

2.00e4 C ×

1 mol e¹⁻

96,500 C

= 0.207 mol e¹⁻

mol e^1–

Next, use the stoichiometric factor from the appropriate half-reaction to determine the moles of copper:

0.104_0__ The half reaction is Cu²⁺ + 2e^1– ⇌ Cu;

0.207 mol e¹⁻ ×

1 mol Cu

2 mol e¹⁻

= 0.104 mol Cu

mol Cu

Finally, use the atomic mass of copper (63.5) to convert moles of copper to grams of copper.

6.58_0__ Alternately, the entire problem could be done as a single factor label problem:

2.00e4 C ×

1 mol e¹⁻

96,500 C

1 mol Cu

2 mol e¹⁻

63.5 g Cu

mol Cu

= 6.58 g Cu

0.1036 mol Cu ×

63.5 g Cu

mol Cu

= 6.58 g Cu

Alternately, the entire problem could be done as a single factor label problem:

2.00e4 C ×

1 mol e¹⁻

96,500 C

1 mol Cu

2 mol e¹⁻

63.5 g Cu

mol Cu

= 6.58 g Cu

g Cu

9.7-3. Electrical Current

1 amp = 1 C/s

Electrical current is the rate at which charge flows through the circuit. It is given the symbol i and has units of amperes (A or amps). One ampere is one coulomb per second (1 A = 1 C/s). Consequently, the charge in coulombs that flows during an electrochemical experiment carried out at a fixed current of i amperes for t seconds is given by Equation 9.8.

( 9.8 )

charge = i × t

Charge is the product of current and time

9.7-4. Mass of Product from Current and Time Exercise

Exercise 9.14:

What mass of gold would be plated on an earring by passing a current of 10. mA through a solution of AuCl₃ for 1.5 hours?

Note: the following steps can be combined into one series of multiplications. The order can be determined using the factor label method.

charge passed = 54_0__ 10. mA = 1.0e–2 C/s

1.5 hr ×

3600 s

1 hr

1.0e−2 C

1 s

= 54 C

moles of electrons passed = 5.6e-4_0__

54 C ×

1 mol e¹⁻

96,500 C

= 5.6e−4 mol e¹⁻

mol e^1–

moles of gold plated = 1.9e-4_0__ Au³⁺ + 3e^1– ⇌ Au

5.6e−4 mol e¹⁻ ×

1 mol Au

3 mol e¹⁻

= 1.9e−4 mol Au

mol Au

mass of gold plated in milligrams = 37_0__ Set up as a single factor-label exercise:

1.5 hr ×

3600 s

1 hr

1.0 e−2 C

1 s

1 mol e¹⁻

96,500 C

1 mol Au

3 mol e¹⁻

197 g Au

mol Au

1000 mg

1 g

= 37 mg Au

atomic weight of Au = 197

1.9e−4 mol Au ×

197 g Au

mol Au

1000 mg

1 g

= 37 mg Au

Or, set up as a single factor-label exercise:

1.5 hr ×

3600 s

1 hr

1.0 e−2 C

1 s

1 mol e¹⁻

96,500 C

1 mol Au

3 mol e¹⁻

197 g Au

mol Au

1000 mg

1 g

= 37 mg Au

mg Au

9.7-5. Time Required for Electrolysis Exercise

Exercise 9.15:

How long (in minutes) should a 5.0 A current be passed through a solution of Ni(NO₃)₂ in order to nickel plate a bathroom fixture with 0.85 g of nickel?

Time in minutes = 9.3_0__

0.85 g Ni ×

1 mol Ni

58.7 g Ni

2 mol e¹⁻

1 mol Ni

96,500 C

1 mol e¹⁻

1 s

5.0 C

1 min

60 s

= 9.3 min

9.8 Exercises and Solutions

Select the links to view either the end-of-chapter exercises or the solutions to the odd exercises.

Fe²⁺ + 2 e^1– ⇌ Fe	ℰ° = –0.44 V
Ni²⁺ + 2 e^1– ⇌ Ni	ℰ° = –0.23 V
Br₂ + 2 e^1– ⇌ 2 Br^1–	ℰ° = +1.09 V
Cl₂ + 2 e^1– ⇌ 2 Cl^1–	ℰ° = +1.39 V

K¹⁺ + 1 e^1– ⇌ K	ℰ° = –2.92 V
2 H₂O + 2 e^1– ⇌ H₂ + 2 OH^1–	ℰ° = –0.41 V
I₂ + 2 e^1– ⇌ 2 I^1–	ℰ° = +0.54 V
O₂ + 4 H¹⁺ + 4 e^1– ⇌ 2 H₂O	ℰ° = +0.88 V

2 H₂O + 2 e^1– ⇌ H₂ + 2 OH^1–	ℰ° = –0.41 V
Cu²⁺ + 2 e^1– ⇌ Cu	ℰ° = +0.34 V
O₂ + 4 H¹⁺ + 4 e^1– ⇌ 2 H₂O	ℰ° = +0.88 V
S₂O₈^2– + 2 e^1– ⇌ 2 SO₄^2–	ℰ° = +2.01 V