Chapter 7 – Mixtures of Acids and Bases
Introduction
In Chapter 6, we examined the equilibrium concentrations in solutions of acids and solutions of bases. In this chapter, we continue our discussion of acids and bases by focusing on the equilibrium concentrations of solutions formed by mixing acids and bases.7.1 The Common-Ion Effect
Introduction
Predicting the effect on an equilibrium mixture caused by the presence of an ion that appears in the equilibrium but is introduced from a separate source is something we will need to do frequently. Qualitative predictions of this type are frequently made with the use of the common ion effect, the topic of this section.Objectives
-
•Explain the common-ion effect and predict the effect of a common ion on an equilibrium mixture.
7.1-1. Definition
When solutions are prepared in such a way that there are two or more separate sources of an ion in an equilibrium, then that ion is referred to as a common ion. In this and the following chapters, we will have the occasion to deal with the effect on an equilibrium mixture caused by the addition of a common ion. The effect of a common ion can readily be predicted with Le Châtelier's principle, which predicts that the composition of the mixture shifts to counteract the addition. Consequently, the common ion effect is summarized as the following:-
•Common Ion Effect: The addition of a common ion to an equilibrium mixture shifts the equilibrium away from the side of the common ion.
7.1-2. Mixture of a Weak Acid and a Strong Acid
We examine the effect that the presence of a strong acid has on the dissociation of a weak acid by considering the dissociation of 0.10 M HClO in water and then in a 0.05 M solution of a strong acid.HClO + H2O ⇌ ClO1− + H3O1+ Ka = 3.5e−8
| HClO | + | H2O | ⇌ | ClO1– | + | H3O1+ | |
|---|---|---|---|---|---|---|---|
| initial | 0.10 | 0 | 0.05 | ||||
| Δ | –x | +x | +x | ||||
| equilibrium | 0.10 – x | x | 0.05 + x |
Ka =
=
| [ClO1−][H3O1+] |
| [HClO] |
| x(0.05 + x) |
| (0.10 − x) |
3.5e−8 =
| x(0.05) |
| (0.10) |
The presence of a strong acid suppresses the dissociation of a weak acid to the point where the strong acid is essentially the sole source of hydronium ions.
7.1-3. Mixture of a Weak Base and a Strong Base
We examine the effect that the presence of a strong base has on the dissociation of a weak base by determining the concentration of HClO in 0.10 M KClO that has been dissolved in water and then in a 0.05 M solution of a strong base.ClO1− + H2O ⇌ HClO + OH1− Kb = 2.9e−7
| ClO1– | + | H2O | ⇌ | HClO | + | OH1– | |
|---|---|---|---|---|---|---|---|
| initial | 0.10 | 0 | 0.05 | ||||
| Δ | –x | +x | +x | ||||
| equilibrium | 0.10 – x | x | 0.05 + x |
Kb =
=
| [HClO][OH1−] |
| [ClO1−] |
| x(0.05 + x) |
| (0.10 − x) |
2.9e−7 =
| x(0.05) |
| (0.10) |
The presence of a strong base suppresses the dissociation of a weak base to the point where the strong base is essentially the sole source of hydroxide ions.
7.2 Buffers
Introduction
In Chapter 6, we discussed four types of acid-base solutions in some detail: strong acid, strong base, weak acid, and weak base. We now discuss buffers, the last type of acid-base solution to be considered. A buffer is defined in the dictionary as a "device that softens the shock of a blow." A chemical buffer serves much the same purpose: it softens the pH change resulting from the addition of a strong acid or base. For example, aspirin is an acid that can upset the stomach, but Bufferin® contains buffers to reduce the pH changes that ordinarily accompany the addition of an acid. Much of the maintenance involved in the upkeep of an aquarium involves maintaining proper buffer levels in the water to assure that the pH stays in a range that is safe for the fish. Blood is also buffered, which is why it maintains a pH of about 7.4 even though many acid-base reactions take place in it. In this section, we discuss the action of buffers.Objectives
-
•Define a buffer and explain how it works.
-
•Choose an appropriate conjugate acid-base pair to use in the preparation of a buffer of a known pH.
-
•Determine the base to acid ratio required to produce a buffer of given pH.
-
•Determine the pH of a buffer given the amounts of acid and base present.
-
•Calculate the change in pH expected when a strong acid or base is added to a buffered solution.
7.2-1. Introduction to Buffers Video
- Viewing the Video
-
•View the video full screen in another window.
-
•Use the video controls to view the video in full screen.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
7.2-2. Definition
A buffer is a solution of a weak acid and its conjugate base in comparable and appreciable amounts. They are able to minimize changes in pH because they contain both a weak acid and a weak base. Thus, if a strong acid is added to a buffered solution, it reacts with the weak base component of the buffer, and if a strong base is added to a buffered solution, it reacts with the weak acid component of the buffer. Either way, the effect of the addition of hydroxide or hydronium ion on the solution is dramatically reduced because these strong acids and bases are converted to much weaker acids and bases by the action of the buffer.7.2-3. Hydronium Ion Concentrations in Buffer Solutions
A buffer contains both the weak acid and the weak base, so both Ka and Kb must be satisfied, and either can be used to determine the composition of the equilibrium mixture. However, because pH is more common than pOH, we use the acid dissociation reaction to discuss buffered solutions because it contains the hydronium ion directly. Consider a hypochlorous acid/hypochlorite ion buffer in which the initial concentrations of the acid (ca) and the base (cb) are comparable. The reaction table for the acid dissociation of acid in the presence of the base has the following form:| HClO | + | H2O | ⇌ | ClO1– | + | H3O1+ | ||
|---|---|---|---|---|---|---|---|---|
| initial | ca | cb | 0 | |||||
| Δ | –x | +x | +x | |||||
| equilibrium | ca – x | cb + x | x |
Ka =
=
| [ClO1−][H3O1+] |
| [HClO] |
| (cb + x)x |
| (ca − x) |
[H3O1+] = x = Ka
= Ka
we obtain the equation that is known as the Henderson-Hasselbalch equation,
where the identity log(x/y) = –log(y/x) has been used. Equation 7.2 is the most common method for determining the pH of a buffer.
| ca |
| cb |
| na |
| nb |
7.2-4. Buffer pH Exercise
Exercise 7.1:
What is the pH of a solution that is 0.600 M potassium acetate and 0.750 M acetic acid?
pKa =
4.74_0__
Acetic acid is HC2H3O2 and has pKa = 4.74

cb =
0.600_0_3_
The concentration of base (acetate ion) is given in the question as 0.600 M.
M

ca =
0.750_0_3_
The concentration of acid (acetic acid) is given in the question as 0.750 M.
M

pH =
4.64_0__

pH = pKa + log
= 4.74 + log
= 4.64
 |
| cb |
| ca |
 |
 |
| 0.600 |
| 0.750 |
 |
7.2-5. Buffer Action Video
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•View the video full screen in another window.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
7.2-6. Buffer Action Against Addition of Base
Buffers act to protect the solution from drastic pH changes resulting from the addition of hydronium or hydroxide ions. They do so by reacting with the added acid or base. However, in order for the buffer to function properly, it must be the excess reactant. Consider the case where x mmol OH1– ion are added to a buffer solution that contains na mmol HClO and nb mmol ClO1–. The strong base reacts extensively with the weak acid in the buffer, so, as long as HClO is in excess, all of the hydroxide reacts. The reaction table has the following form:| HClO | + | OH1– | ⇌ | ClO1– | + | H2O | ||
|---|---|---|---|---|---|---|---|---|
| initial | na | x | nb | 0 | ||||
| Δ | –x | –x | +x | +x | ||||
| equilibrium | na – x | ~0 | nb + x | x |
pH = pKa + log
= pKa + log
can still be used to determine its pH.
 |
| cb |
| ca |
 |
 |
| nb |
| na |
 |
7.2-7. Strong Base–Buffer Worked Example
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•View the video full screen in another window.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
7.2-8. Buffer Action with Strong Base Exercise
Exercise 7.2:
In a previous exercise, we determined that the pH of a buffer that is 0.600 M potassium acetate and
0.750 M acetic acid is 4.64.
0.750 M acetic acid is 4.64.
What is the pH of a solution prepared by adding 10. mL of 6.0 M NaOH to 200. mL of this buffer?
First, complete the reaction table for the reaction of the weak acid with the strong base. Note that all entries are in mmol. (Refer to the Acid-Base Table with pKa and Equation 7.2
pH = pKa + log
= pKa + log
. Indicate any subscripted characters with an underscore (_) and any superscripted characters with a caret (^). For example, NH_4^1+ for NH41+.)
 |
| cb |
| ca |
 |
 |
| nb |
| na |
 |
| Reacting Acid | + | Reacting Base | → | Produced Base | + | Produced Acid | ||
|---|---|---|---|---|---|---|---|---|
|
o_HC_2H_3O_2_s
The addition of strong base causes the acid component of the buffer to react. Acetic acid (HC2H3O2) is the reacting acid.
|
+ |
o_OH^1-_s
NaOH is a strong base, so the reacting base is OH1–.
|
→ |
o_C_2H_3O_2^1-_s
The conjugate base of acetic acid is the acetate ion. Thus, C2H3O21– is the produced base.
|
+ |
o_H_2O_s
H2O is the conjugate acid of is OH1–.
|
||
| initial |
150_0__
(0.750 M)(200. mL) = 150. mmol
|
60_0__
(6.0 M)(10. mL) = 60. mmol
|
120_0__
(0.600 M)(200. mL) = 120. mmol
|
mmol | ||||
| Δ |
-60_0__
The reaction is extensive, so all 60. mmol of base react.
|
-60_0__
The reaction is extensive, so all 60. mmol of base react.
|
+60_0__
The reaction is extensive, so all 60 mmol of base react.
|
mmol | ||||
| equilibrium |
90_0__
150. mmol initially – 60. mmol react = 90. mmol remain
|
0_0__
60. mmol initially – 60. mmol react = 0 mmol remain
|
180_0__
120. mmol initially + 60. mmol form = 180. mmol remain
|
mmol |
pH =
5.04_0__

4.74 + log
= 5.04
 |
| 180 mmol base |
| 90 mmol acid |
 |
7.2-9. Buffer Action Against Addition of Acid
Consider the case where x mmol of H3O1+ ions are added to a buffer solution that contains na mmol HClO and nb mmol ClO1–. The strong acid reacts extensively with the weak base in the buffer, so, as long as ClO1– is in excess, all of the hydronium reacts. The reaction table has the following form:| ClO1– | + | H3O1+ | ⇌ | HClO | + | H2O | ||
|---|---|---|---|---|---|---|---|---|
| initial | nb | x | na | 0 | ||||
| Δ | –x | +x | +x | |||||
| equilibrium | nb – x | ~0 | na + x | x |
pH = pKa + log
= pKa + log
can still be used to determine its pH.
 |
| cb |
| ca |
 |
 |
| nb |
| na |
 |
7.2-10. Buffer Action with Strong Acid Exercise
Exercise 7.3:
What is the pH of a solution prepared by adding 10. mL of 6.0 M HCl to 200. mL of the buffer?
Complete the reaction table for the reaction of the weak base with the strong acid in millimoles. (Refer to the Acid-Base Table with pKa and Equation 7.2
pH = pKa + log
= pKa + log
. Indicate any subscripted characters with an underscore (_) and any superscripted characters with a caret (^). For example, NH_4^1+ for NH41+.) |
| cb |
| ca |
 |
 |
| nb |
| na |
 |
| Reacting Base | + | Reacting Acid | → | Produced Acid | + | Produced Base | ||
|---|---|---|---|---|---|---|---|---|
|
o_C_2H_3O_2^1-_s
The addition of strong acid causes the base component of the buffer to react, so the acetate ion (C2H3O21–) is the reacting base.
|
+ |
o_H_3O^1+_s
HCl is a strong acid, so the reacting base is H3O1+.
|
→ |
o_HC_2H_3O_2_s
The conjugate acid of the acetate ion is acetic acid. Thus, HC2H3O2 is the produced acid.
|
+ |
o_H_2O_s
H2O is the conjugate base of H3O1+.
|
||
| initial |
120_0_3_
(0.600 M)(200. mL) 120. mmol
|
60_0_2_
(6.0 M)(10. mL) = 60. mmol
|
150_0_3_
(0.750 M)(200. mL) = 150. mmol
|
mmol | ||||
| Δ |
-60_0_2_
All 60. mmol [H3O1+] react.
|
-60_0_2_
All 60. mmol [H3O1+] react.
|
+60_0_2_
All 60. mmol [H3O1+] react.
|
mmol | ||||
| equilibrium |
60_0_2_
120. mmol initially – 60. mmol react = 60. mmol
|
0_0__
60. mmol initially – 60. mmol react = 0
|
210_0_3_
150. mmol initially + 60. mmol form = 210. mmol
|
mmol |
pH =
4.20_0_3_

4.74 + log
= 4.20
 |
| 60. mmol base |
| 210. mmol acid |
 |
7.2-11. Buffer Exercise
Exercise 7.4:
A buffer is prepared by dissolving 23.5 g of KNO2 (Mm = 85.1 g·mol–1) in 1.25 L of 0.0882 M HNO2.
(a) What is the pH of the buffer?
na =
0.110_0_3_
(1.25 L)(0.0882 M) = 0.110 mol
mol

nb =
0.276_0__

23.5 g KNO2
= 0.276 mol KNO2
mol
| 1 mol KNO2 |
| 85.1 g KNO2 |
pKa =
3.40_0_3_
This is given in the Acid-Base Table with pKa as 3.40

pH =
3.80_0_3_

3.40 + log
= 3.80
 |
| 0.276 mol base |
| 0.110 mol acid |
 |
(b) What would be the pH of the buffer solution after the addition of 22.8 mL of 1.45 M NaOH?
(Indicate any subscripted characters with an underscore (_) and any superscripted characters with a caret (^). For example, NH_4^1+ for NH41+.)
| Reacting Acid | + | Reacting Base | → | Produced Base | + | Produced Acid | ||
|---|---|---|---|---|---|---|---|---|
|
o_HNO_2_s
The addition of strong base causes the acid component of the buffer to react. Nitrous acid (HNO2) is the reacting acid.
|
+ |
o_OH^1-_s
NaOH is a strong base, so the reacting base is OH1–.
|
→ |
o_NO_2^1-_s
The conjugate base of nitrous acid is the nitrite ion. Thus, NO21– is the produced base.
|
+ |
o_H_2O_s
H2O is the conjugate acid of the reacting base, OH1–.
|
||
| initial |
0.110_0_3_
See the first part.
|
0.0331_0__
(1.45 M)(0.0228 mL) = 0.0331 mol
|
0.276_0__
See the first part.
|
mol | ||||
| Δ |
-0.0331_0__
All 0.0331 mol OH1– reacts.
|
-0.0331_0__
All 0.0331 mol OH1– reacts.
|
+0.0331_0__
All 0.0331 mol OH1– reacts.
|
mol | ||||
| equilibrium |
0.077_0__
0.110 mol initially – 0.0331 mol react = 0.077 mol
|
0_0__
0.0331 mol initially – 0.0331 mol react = 0 mol
|
0.309_0__
0.276 mol initially + 0.0331 mol form = 0.309 mol
|
mol |
Use Equation 7.2
pH = pKa + log
= pKa + log
to determine the pH. |
| cb |
| ca |
 |
 |
| nb |
| na |
 |
pH =
4.00_0_3_

3.40 + log
= 4.00
 |
| 0.309 mol base |
| 0.077 mol acid |
 |
7-2.12. Buffer Capacity
There must be appreciable amounts of the acid and its conjugate base in a buffer to assure that it has acceptable buffer capacity, which is the amount of acid or base that can be added without destroying the effectiveness of the buffer. Thus, a buffer solution has a large buffer capacity if it contains a large number of moles of the weak acid and of the weak base.7.2-13. Buffer Range
A buffer functions well when the addition of large amounts of acid or base result in only small pH changes. The pH range over which the buffer is effective is called the buffer range. Figure 7.1 shows the relationship between pH of an acetic acid/acetate ion buffer and the mole fractions of the acid and the base. The buffer range is the pH range over which the mole fractions change most dramatically with pH (highlighted by the box in the figure).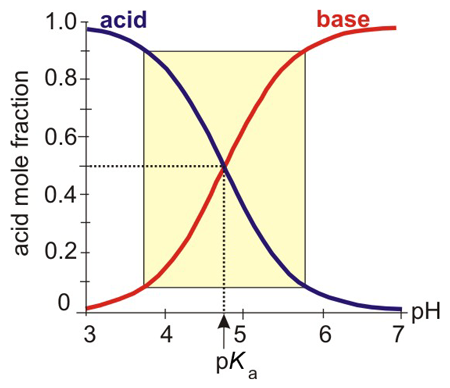
Figure 7.1: Effective Buffer Range
The mole fractions of acetic acid and its conjugate base as a function of pH. The effective buffer range is indicated by the box. The pH of a buffer solution in which the two mole fractions are equal is equal to the pKa of the acid.
pH = pKa + log
= pKa + log
and log 1 = 0 to the midpoint indicates that pH = pKa. Thus, buffers are most effective at pH values near their pKa.
As shown in Figure 7.1, buffers operate acceptably in the range where the mole fraction of the acid or base is in the range of 0.1 to 0.9, which means that 0.1 < ca/cb < 10.
 |
| cb |
| ca |
 |
 |
| nb |
| na |
 |
We conclude that a buffer is effective at a pH that is within one pH unit of its pKa.
7.2-14. Preparing a pH = 7 Buffer Exercise
Exercise 7.5:

How would you prepare a pH = 7.00 buffer?
First, select the best buffer system for this pH.
-
H3PO4/H2PO41– pKa = 2.12 The best acid/base pair is the one with the acid that has a pKa closest to the desired pH.
-
HNO2/NO21– pKa = 3.40 The best acid/base pair is the one with the acid that has a pKa closest to the desired pH.
-
H2PO41–/HPO42– pKa = 7.21
-
NH41+/NH3 pKa = 9.25 The best acid/base pair is the one with the acid that has a pKa closest to the desired pH.
-
HPO42–/PO43– pKa = 12.32 The best acid/base pair is the one with the acid that has a pKa closest to the desired pH.

log(nb/na) =
-0.21_0__

log
= pH − pKa = 7.00 − 7.21 = −0.21
 |
| nb |
| na |
 |
Take the antilog to obtain the ratio.
nb/na =
0.62_0__
= 10−0.21 = 0.62 mol base/mol acid

| nb |
| na |
Assume you have 1.50 L of a 0.840 M solution of the acid and determine the number of moles of base that would have to be added to produce the buffer.
moles of acid present =
1.26_0__
na = (0.840 M)(1.50 L) = 1.26 mol
mol

moles of base present =
0.78_0__

na ×
= 1.26 mol acid × 0.62 mol base/mol acid = 0.78 mol base
mol
| nb |
| na |
7.2-15. Preparing a pH = 9.8 Buffer Exercise
Exercise 7.6:

How many moles of base should be added to 500. mL of 0.222 M acid to prepare a pH = 9.80 buffer solution?
First, select the best buffer system for this pH.
-
H3PO4/H2PO41– pKa = 2.12 The best acid/base pair is the one with the acid that has a pKa closest to the desired pH.
-
HNO2/NO21– pKa = 3.40 The best acid/base pair is the one with the acid that has a pKa closest to the desired pH.
-
H2PO41–/HPO42– pKa = 7.21 The best acid/base pair is the one with the acid that has a pKa closest to the desired pH.
-
NH41+/NH3 pKa = 9.25
-
HPO42–/PO43– pKa = 12.32 The best acid/base pair is the one with the acid that has a pKa closest to the desired pH.

log(nb/na) =
0.55_0__

log
= pH − pKa = 9.80 − 9.25 = 0.55
 |
| nb |
| na |
 |
Take the antilog to obtain the ratio.
nb/na =
3.5_0__
= 10+0.55 = 3.5 mol base/mol acid

| nb |
| na |
Determine the number of moles of base that would have to be added to the acid.
moles of acid =
0.111_0__
na = (0.222 M)(0.500 L) = 0.111 mol acid
mol

moles of base =
0.39_0__

nb ×
= 0.111 mol acid × 3.5 mol base/mol acid = 0.39 mol base
mol
| nb |
| na |
7.3 Acid-Base Composition from Reactant Amounts
Introduction
We have now treated five different types of acid-base solutions and shown how to determine [H3O1+], [OH1–], and pH of each:-
1Strong acid: Strong acids dissociate completely, so [H3O1+] = co.
-
2Strong base: Strong bases (M(OH)n) dissociate completely, so [OH1–] = nco.
-
3Weak acid: Solve the Ka expression for [H3O1+] using Equation 6.6.
-
4Weak base: Solve the Kb expression for [OH1–] using Equation 6.9.
-
5Buffers: Solve the Ka expression for [H3O1+] using Equation 7.1[H3O1+] = x = Kaor solve directly for pH using Equation 7.2
= Kaca cb na nb pH = pKa + log.
cb ca
= pKa + log

nb na 
-
1weak acid–weak base
-
2strong acid–strong base
-
3weak acid–strong base
-
4strong acid–weak base
Objectives
-
•Write acid-base reactions and determine their equilibrium constants from the Ka's of the reacting and produced acids.
-
•Determine the concentrations of all species in a solution prepared by mixing a strong acid (or base) with a strong base (or acid) or a weak base (or acid).
Weak Acid–Weak Base Reactions
7.3-1. The Equilibrium Constant
Consider the following reaction.HF + OCl1− → F1− + HOCl
K =
| [F1−][HOCl] |
| [HF][OCl1−] |
| Ka (HF) |
| Ka (HOCl) |
| [H3O1+][F1−] |
| [HF] |
| [HOCl] |
| [H3O1+][OCl1−] |
| [F1−][HOCl] |
| [HF][OCl1−] |
K =
=
= 2.1e+4
| Ka of reacting acid HF |
| Ka of produced acid HOCl |
| 7.2e–4 |
| 3.5e–8 |
7.3-2. Determining K Exercise
Exercise 7.7:
Determine the value of K for the following aqueous weak acid–weak base reactions.
| Reaction |
Ka (reacting acid) |
Ka (produced acid) |
K | ||
|---|---|---|---|---|---|
|
HNO2 + F1− ⇌ NO21− + HF
|
4.0e-4_0_2_
HNO2 is the reacting acid with a Ka = 4.0e–4
|
7.2e-4_0__
HF is the produced acid with a Ka = 7.2e–4
|
0.56_0__
K =
|
||
|
HCN + CH3COO1− ⇌ CN1− + CH3COOH
|
4.0e-10_0_2_
HCN is the reacting acid with a Ka = 4.0e–10
|
1.8e-5_0__
CH3COOH is the produced acid with a Ka = 1.8e–5
|
2.2e-5_0__
K =
|
||
|
NH3 + HSO41− ⇌ NH41+ + SO42−
|
1.2e-2_0__
HSO41– is the reacting acid with a Ka = 0.012
|
5.6e-10_0__
NH41+ is the produced acid with a Ka = 5.6e–10
|
2.1e7_0__
K =
|
7.3-3. Mixing Exercise
Exercise 7.8:
Take the square root of both sides:
Multiply both sides by (0.050 – x) to get 0.037 – 0.75x = x and solve: x = 0.037/1.75 = 0.021 M M
What is the NO21– ion concentration in a solution prepared by mixing 75 mL of 0.10 M HNO2 and 75 mL of 0.10 M KF? Fill in the reaction table with molar concentration, and use x to indicate the final concentration of NO21–. (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a caret (^). For example, NH_4^1+ for NH41+.)
K =
0.56_0__

K =
=
= 0.56
| Ka (HNO2) |
| Ka (HF) |
| 4.0e−04 |
| 7.2e−04 |
The reaction table:
| Reacting Acid | + | Reacting Base | → | Produced Base | + | Produced Acid | ||
|---|---|---|---|---|---|---|---|---|
|
o_HNO_2_s
The reacting acid is HNO2.
|
+ |
o_F^1-_s
The reacting acid is F1–.
|
→ |
o_NO_2^1-_s
The reacting acid is NO21–.
|
+ |
o_HF_s
The reacting acid is HF.
|
||
| initial |
0.050_0_2_
The given concentration is diluted 1:2 by mixing.
|
0.050_0_2_
The given concentration is diluted 1:2 by mixing.
|
0_0__
There is none initially.
|
0_0__
There is none initially.
|
mol | |||
| Δ |
o_-x_s
K is not large so the amount that reacts is unknown. Reactants disappear and stoichiometry is 1:1:1:1.
|
o_-x_s
K is not large so the amount that reacts is unknown. Reactants disappear and stoichiometry is 1:1:1:1.
|
o_+x_s
Use x as the amount of nitrite that forms.
|
o_+x_s
The amount of HF that forms is the same as the amount of nitrite ion.
|
mol | |||
| equilibrium |
o_0.050-x_s
Add the initial and Δ lines to obtain
0.050−x .
|
o_0.050-x_s
Add the initial and Δ lines to obtain
0.050−x .
|
o_x_s
Add the initial and Δ lines to obtain
x .
|
o_x_s
Add the initial and Δ lines to obtain
x .
|
mol |
Set up the equilibrium constant expression. It is a perfect square, so take the square root of both sides to determine the answer.
[NO21−]
=
0.021_0__
0.56 =
=
| [HNO2][F1−] |
| [NO21−][HF] |
| x2 |
| (0.050 − x)2 |
Take the square root of both sides:
0.75 =
| x |
| (0.050 − x) |
Multiply both sides by (0.050 – x) to get 0.037 – 0.75x = x and solve: x = 0.037/1.75 = 0.021 M M
7.3-4. Overview of Extensive Reactions
The remainder of the acid-base reaction types all involve a strong acid and/or a strong base, so they are all extensive. Consequently, the limiting reactant is assumed to disappear completely, which means that there are no unknowns in the reaction table. We will use the following method in each case:-
1Write the chemical equation and construct the reaction table. We will use millimoles in the reaction table because the volumes are all given in milliliters, but molarities can also be used.
-
2Identify the type of solution that results from the mixing based upon the equilibrium entries.
-
•Strong acid if the entry under [H3O1+] is not zero. There can be no base present if there is some H3O1+ because they would react, and a weak acid can be ignored in the presence of a strong acid.
-
•Strong base if the entry under OH1– is not zero. There can be no acid present if there is some OH1– because they would react, and a weak base can be ignored in the presence of a strong one.
-
•Weak acid if the only nonzero entry lies under a weak acid.
-
•Weak base if the only nonzero entry lies under a weak base.
-
•Buffer if the entries under both the weak acid and its conjugate base are nonzero.
-
-
3Determine [H3O1+], [OH1–], pH, or pOH using the equation appropriate to the solution type above.
7.3-5. Titration Curves
Recall from Section 2.4-5. that the equivalence point in an acid-base titration is that point where the number of moles of analyte in the initial flask equals the number of moles of titrant that are added, which is summarized as follows.-
•Equivalence Point: moles acid = moles base, so MacidVacid = MbaseVbase
Strong Acid–Strong Base Reactions
7.3-6. Strong Acid–Strong Base Titration Video
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•View the video full screen in another window.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
7.3-7. Method
Our first titration curve is for the titration of a strong acid with a strong base. We start out with na moles of acid and determine the pH after nb moles of base have been added. The reaction is extensive, so there is essentially no limiting reactant present at equilibrium and the solution type is dictated solely by the reactant in excess. The solution type depends upon the relative values of na and nb, and the following reaction table shows the case where the base is the limiting reactant:| H3O1+ | + | OH1– | → | H2O | + | H2O | |
|---|---|---|---|---|---|---|---|
| initial | na | nb | |||||
| Δ | –nb | –nb | |||||
| equilibrium | na – nb | ~0 |
| Moles | Solution Type | Moles of Excess Reactant | |
|---|---|---|---|
| na > nb | strong acid | na – nb mol H3O1+ | pH = –log [H3O1+] |
| na = nb | neutral | no excess reactant | pH = 7.00 |
| na < nb | strong base | nb – na mol OH1– | pOH = –log [OH1–] |
Table 7.1: Solution Types Resulting From Mixing a Strong Acid and a Strong Base Solution type resulting from the reaction of na moles of a strong acid with nb moles of a strong base.
7.3-8. SA–SB Titration Curve Exercise
Exercise 7.9:
A strong acid–strong base titration curve is shown below. The equivalence point (yellow circle) in a strong acid–strong base titration is pure water, so the pH is 7.00.
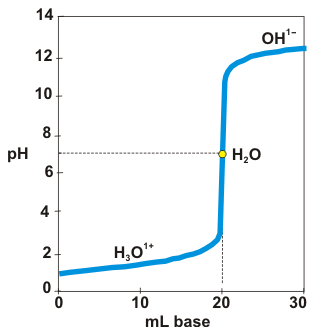

Determine the pH after the addition of 10.0 mL, 20.0 mL, and 30.0 mL of base in the titration of 20.0 mL of 0.100 M HCl with 0.100 M NaOH.
Put the number of millimoles of excess reactant present at equilibrium in the "xs" line or 0 if neither reactant is in excess.
| 10.0 mL base | 20.0 mL base | 30.0 mL base | ||
|---|---|---|---|---|
| na |
2.00_0_3_
na = MV = (0.100 M)(20.0 mL)
|
2.00_0_3_
na = MV = (0.100 M)(20.0 mL)
|
2.00_0_3_
na = MV = (0.100 M)(20.0 mL)
|
mmol |
| nb |
1.00_0_3_
nb = MV = (0.100 M)(10.0 mL)
|
2.00_0_3_
nb = MV = (0.100 M)(20.0 mL)
|
3.00_0_3_
nb = MV = (0.100 M)(30.0 mL)
|
mmol |
| xs |
1_0_3_
na > nb, so there are na – nb mmol H3O1+.
|
0_0__
na = nb, so neither is in excess.
|
1.00_0_3_
na < nb, so there are nb – na mmol OH1–.
|
mmol |
| total volume |
30.0_0_3_
20.0 mL of acid + 10.0 mL of base.
|
40.0_0_3_
20.0 mL of acid + 20.0 mL of base.
|
50.0_0_3_
20.0 mL of acid + 30.0 mL of base.
|
mL |
| xs concentration |
0.0333_0__
[H3O1+] = 1.00 mmol/30.0 mL.
|
1.0e-7_0_2_
[H3O1+] = [OH1–] = 1.0e–7 M.
|
0.0200_0_3_
[OH1–] = 1.00 mmol/50.0 mL.
|
M |
| pH |
1.478_0__
pH = –log(0.0333)
|
7.00_0_2_
pH = –log(1.0e–7)
|
12.30_0_4_
pOH = –log(0.0200); pH = 14.00 – pOH
|
mmol |
Weak Acid–Strong Base Reactions
7.3-9. Weak Acid–Strong Base Titration Video
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•View the video full screen in another window.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
7.3-10. Weak Acid–Strong Base Titration Calculations
We now examine the titration curve for the titration of na moles of a weak acid HA with hydroxide ion. Initially the solution is one of the weak acid HA, so if less than 5% of the acid reacts, we can write where c is the concentration of HA. OH1– is limiting reactant. The reaction table has the following form:| HA | + | OH1– | → | A1– | + | H2O | |
|---|---|---|---|---|---|---|---|
| initial | na | nb | 0 | ||||
| Δ | –nb | –nb | +nb | ||||
| equilibrium | na – nb | ~0 | nb |
| HA | + | OH1– | → | A1– | + | H2O | |
|---|---|---|---|---|---|---|---|
| initial | na | na/2 | 0 | ||||
| Δ | –na/2 | –na/2 | +na/2 | ||||
| equilibrium | na/2 | ~0 | na/2 |
The pH at the midpoint of a titration of a weak acid with a strong base is equal to the pKa of the acid.
| HA | + | OH1– | → | A1– | + | H2O | |
|---|---|---|---|---|---|---|---|
| initial | n | n | 0 | ||||
| Δ | –n | –n | +n | ||||
| equilibrium | ~0 | ~0 | n |
| HA | + | OH1– | → | A1– | + | H2O | |
|---|---|---|---|---|---|---|---|
| initial | na | nb | 0 | ||||
| Δ | –na | –na | +na | ||||
| equilibrium | ~0 | nb – na | na |
7.3-11. WA–SB Titration Curve Exercise
Exercise 7.10:




Determine the pH at points (a)–(d) in the titration curve of 20.0 mL of 0.100 M HC2H3O2 with 0.100 M NaOH shown below. The orange rectangle outlines the buffer region.
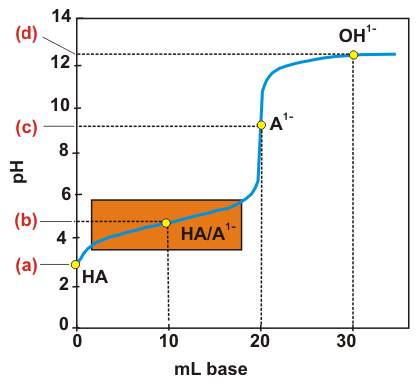

na =
2.00_0_3_
na = MaVa = (0.100 M)(20.0 mL)
mmol acid initially

point (a) 0 mL (nb = 0 – weak acid)
[H3O1+]
=
1.3e-3_0_2_
a weak acid solution, so [H3O1+] =
=
M
 | Kac |
 | (1.8e−5)(0.100) |
pH =
2.87_0_3_
pH = –log[H3O1+]

point (b) 10.0 mL (0 < nb < na: buffer)
nb =
1.00_0_3_
nb = MbVb = (0.100 M)(10.0 mL)
mmol base added

weak acid remaining =
1.00_0_3_
acid remaining = initial acid – acid reacting = na – nb
mmol

weak base produced =
1.00_0_3_
All of the added hydroxide is converted into the weak base.
mmol

pH =
4.74_0_3_

pH = pKa + log
= 4.74 + log
= 4.74
 |
| nb |
| na |
 |
 |
| 1.00 mmol base |
| 1.00 mmol acid |
 |
point (c) 20.0 mL (nb = na: equivalence point, weak base)
nb =
2.00_0_3_
nb = MbVb = (0.100 M)(20.0 mL)
mmol base added

weak acid remaining =
0.00_0__
acid remaining = initial acid – acid reacting = na – nb
mmol

weak base produced =
2.00_0_3_
All of the added hydroxide is converted into the weak base.
mmol

[CH3COO1−]
=
0.0500_0_3_
2.00 mmol of base are present in 20.0 + 20.0 mL
M
[OH1−]
=
5.3e-6_0_2_
[OH1−] =
=
M
 | Kbc |
 | (5.6e−10)(0.050) |
pH =
8.72_0_3_
pH = 14.00 – pOH

point (d) 30.0 mL (nb > na: strong base)
nb =
3.00_0_3_
nb = MbVb = (0.100 M)(30.0 mL)
mmol base added

excess OH1– =
1.00_0_3_
base added – base reacting = nb – na
mmol

[OH1−]
=
0.0200_0_3_
total volume = 20.0 mL + 30.0 mL
M
pH =
12.30_0_4_
pH = 14.00 – pOH

7.3-12. Using a Titration Curve Exercise
Exercise 7.11:

Consider the titration curve for the titration of 50.00 mL of an unknown weak acid with 0.122 M NaOH that is shown below.
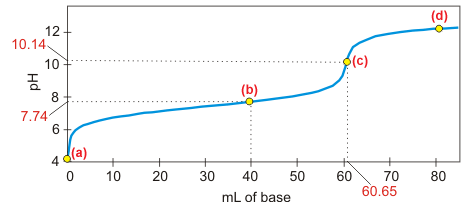

Determine the concentration of the weak acid and its pKa.
volume of base at the equivalence point:
60.65_0__
Point (c) is the equivalence point.
mL

mmol base added at equivalence point:
7.40_0_3_
n = MV = (0.122 M)(60.65 mL)
mmol

mmol acid present initially:
7.40_0_3_
mmoles base added = mmoles initial acid
mmol

concentration of original acid:
0.148_0__
M = n/V = (7.40 mmol)(50.00 mL)

The solution type at point (b) is which of the following?
-
weak acid Both the acid and its base are present up to the equivalence point.
-
strong base Both the acid and its base are present up to the equivalence point.
-
weak base Both the acid and its base are present up to the equivalence point.
-
buffer

mmol of hydroxide added at point (b) =
4.88_0__
n = MV = (0.122 M)(40.00 mL)
mmol

equilibrium mmol weak acid at point (b) =
2.52_0__
7.40 mmol initially, but 4.88 mmol react with the added hydroxide
mmol

equilibrium mmol conjugate base at point (b) =
4.88_0__
All of the added hydroxide is converted into the conjugate base.
mmol

pKa =
7.45_0__
pH = 7.74 = pKa + log(nb/na) at point (b).

7.3-13. The Shape of an Acid-Strong Base Titration Curve
The general shape of a titration curve consists of a sharp rise in pH in the vicinity of the equivalence point, but how steep the slope of the rise is depends upon the strength of the acid. Compare the titration curves for the titrations of 0.1 M HCl, 0.1 M HC2H3O2, and 0.1 M HCN. In each case, the final pH approaches the pH of the strong base, which would be 13.0 in the case of 0.1 M NaOH. However, the pH at the midpoint of the titration varies with the acid strength. Thus, the pH is about 1.5 at the midpoint in the titration of 0.10 M HCl, but it equals the pKa of the acid for a weak acid, which is 4.74 for HC2H3O2 and 9.40 for HCN. Thus, the rise of the curve in the case of a strong acid is about 12 pH units, but it is only about 8 pH units for HC2H3O2 and about 3 pH units for HCN. The less dramatic change in pH associated with very weak acids can make it difficult to get as a precise determination of the equivalence point.7.3-14. Mixing Exercise
Exercise 7.12:



What is the pH of a solution prepared by mixing 34.0 mL of 0.250 M NaOH and 16.5 mL of 0.515 M KHSO4?
The reaction table:
| HSO41– | + | OH1– | ⇌ | SO42– | + | H2O | ||
|---|---|---|---|---|---|---|---|---|
| initial |
8.50_0_3_
na = MaVa = (0.515 M)(16.5 mL) = 8.50 mmol
|
8.50_0_3_
nb = MbVb = (0.250 M)(34.0 mL) = 8.50 mmol
|
0_0__
There is none initially.
|
mmol | ||||
| Δ |
-8.50_0_3_
8.50 mmol of limiting reactant reacts.
|
-8.50_0_3_
8.50 mmol of limiting reactant reacts.
|
+8.50_0__
8.50 mmol of limiting reactant reacts.
|
mmol | ||||
| equilibrium |
0_0__
8.50 mmol initially – 8.50 mmol react = 0.
|
0_0__
8.50 mmol initially – 8.50 mmol react = 0.
|
8.50_0_3_
0 mmol initially + 8.50 mmol form = 8.50 mmol.
|
mmol |
The resulting solution type is which of the following?
-
weak acid Which reactant has a nonzero entry in the reaction table?
-
strong base Which reactant has a nonzero entry in the reaction table?
-
weak base
-
buffer Which reactant has a nonzero entry in the reaction table?

[SO42−]
=
0.168_0__
[SO42−] =
= 0.168 M
M
| 8.50 mmol SO42− |
| 50.5 mL solution |
Kb =
8.3e-13_0__

Kb =
=
= 8.3e−13
| Kw |
| Ka |
| 1.0e−14 |
| 0.012 |
[OH1−]
=
3.7e-7_0__
[OH1–] = [(0.168)(8.3e–13)]1/2 = 3.7e–07 M
M
pH =
7.57_0_3_
pOH = –log [OH1–] = –log(3.7e–07) = 6.43
pH = 14.00 – pOH = 14.00 – 6.43 = 7.57
pH = 14.00 – pOH = 14.00 – 6.43 = 7.57
7.3-15. Polyprotic Acid–Strong Base Titration Video
- Viewing the Video
-
•View the video in this window by selecting the play button.
-
•View the video full screen in another window.
-
•View the video in text format by scrolling down.
-
•Jump to the exercises for this topic.
7.3-16. Polyprotic Acid–Strong Base
Polyprotic acids dissociate one proton at a time, and they are deprotonated by OH1– ion one proton at a time. The loss of each proton gives rise to one equivalence point. The equilibrium constants for the individual dissociations are usually very different, so only one or two species usually have non-negligible concentrations in polyprotic acid solutions. Indeed, their equilibria are identical to those of monoprotic acids except that the base may be amphiprotic. Consider the titration of H2A with a strong base. The following reaction table covers the reaction up to the first equivalence point.| H2A | + | OH1– | → | HA1– | + | H2O | ||
|---|---|---|---|---|---|---|---|---|
| initial | na | nb | 0 | mmol | ||||
| Δ | –nb | –nb | +nb | mmol | ||||
| equilibrium | na – nb | ~0 | +nb | mmol |
| HA1– | + | OH1– | → | A2– | + | H2O | ||
|---|---|---|---|---|---|---|---|---|
| intial | na | nb | 0 | mmol | ||||
| Δ | –nb | –nb | +nb | mmol | ||||
| equilibrium | na – nb | ~0 | +nb | mmol |
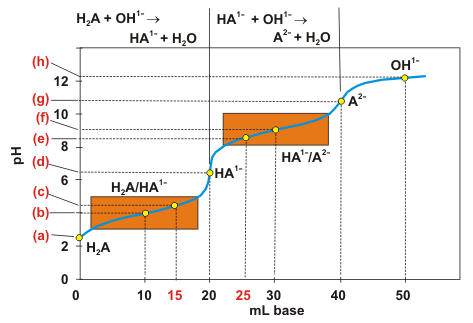
Figure 7.2: Diprotic acid–Strong base Titration Curve
The rectangles outline the two buffer ranges. The points on the graph represent the following: (a) weak acid H2A; (b) 1st midpoint so pH = pK1; (c) H2A/HA1– buffer; (d) 1st equivalence point, amphiprotic HA1–; (e) HA1–/A2– buffer; (f) 2nd midpoint so pH = pK2; (g) 2nd equivalence point, weak base A2–; and (h) strong base solution.
7.3-17. Polyprotic Titration Curve Exercise
Exercise 7.13:
Determine the pH at various points in the titration curve for the titration of 20.0 mL of 0.100 M H2A (pK1 = 4.00, pK2 = 9.00) with 0.100 M NaOH. The titration curve is shown in Figure 7.2. You should construct a reaction table at each point, determine the solution type, and then the pH.
na =
2.00_0_3_
n = MV = (0.100 M)(20.0 mL)
mmol

point (b) 10.0 mL (midway to first equivalence point)
pH =
4.00_0_3_
This is the midpoint to the first endpoint in the titration, so pH = pK1.

point (c) 15.0 mL (buffer region of first equivalence point)
nb =
1.50_0_3_
n = MV = (0.100 M)(15.0 mL)
mmol

eq mmol H2A =
0.50_0_2_
n = mmol acid added – mmol acid reacting = 2.00 – 1.50
mmol

eq mmol HA1– =
1.50_0_3_
mmol of weak base at equilibrium = mmol of strong base added if strong base is limiting reactant
mmol

pH =
4.48_0__
Both the acid and base are present, so this is a buffer solution.
pH = 4.00 + log(1.50/0.50)
pH = 4.00 + log(1.50/0.50)
point (d) 20.0 mL (solution of amphiprotic substance HA1–)
pH =
6.50_0_3_
Use Equation 6.13 to get the pH of the solution of an amphiprotic substance, HA1–.
pH = 1/2(pK1 + pK2)
pH = 1/2(pK1 + pK2)
point (e) 25.0 mL (buffer region of second equivalence point)
nb =
0.50_0_2_
The first equivalence point was at 20 mL, so this point is only 5 mL past it. Thus, only 5 mL of base has been added to react with HA1–.
n = MV = (0.100 M)(5.0 mL) mmol from first eq point
n = MV = (0.100 M)(5.0 mL) mmol from first eq point
eq mmol HA1– =
1.50_0_3_
HA1– is now the acid, and there were 2.00 mmol when it starts to react with the base at the first equivalence point. The number of mmoles present is determined to be n = initial mmol acid – mmol acid reacting = 2.00 – 0.50
mmol

eq mmol A2– =
0.50_0_2_
mmol of weak base at equilibrium = mmol of strong base added if strong base is limiting reactant.
mmol

pH =
8.52_0__
Both the acid and base are present, so this is a buffer solution for the second titration.
pH = 9.00 + log(0.50/1.50)
pH = 9.00 + log(0.50/1.50)
point (f) 30.0 mL (midway to second equivalence point)
pH =
9.00_0_3_
The pH at the midpoint between the first and second equivalence points equals pK2.

Strong Acid–Weak Base Reactions
7.3-18. Summary of Strong Acid–Weak Base Reactions
The reaction between a strong acid and a weak base is treated analogously with that between a weak acid and a strong base. The nature of the resulting solution depends upon the relative number of moles of acid (na) and base (nb). na < nb: acid is limiting reactant| H3O1+ | + | A1– | → | HA | + | H2O | ||
|---|---|---|---|---|---|---|---|---|
| equilibrium | ~0 | nb – na | na | Buffer |
| H3O1+ | + | A1– | → | HA | + | H2O | ||
|---|---|---|---|---|---|---|---|---|
| equilibrium | ~0 | ~0 | n | Weak Acid |
| H3O1+ | + | A1– | → | HA | + | H2O | ||
|---|---|---|---|---|---|---|---|---|
| equilibrium | na – nb | ~0 | na | Strong Acid |
7.3-19. Strong Acid–Weak Base Titration
Thank you for your patience as this section undergoes re-construction.7.3-20. Strong Acid–Weak Base Titration Curve
Exercise 7.14:
Determine the pH at each of the following points in the titration curve for the titration of 20.0 mL of 0.100 M NH3 with 0.100 M HCl.
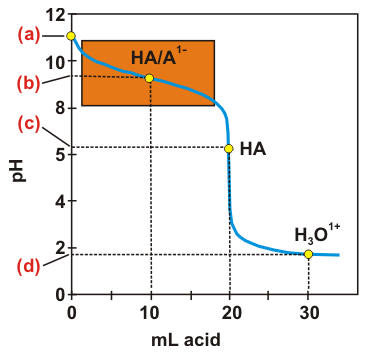

-
(a)na = 0: a solution of the weak base NH3.
-
(b)na < nb: a buffer solution. pH = pKa at point (b).
-
(c)na = nb: the equivalence point is a solution of the weak acid HA.
-
(d)na > nb: excess H3O1+ makes the solution a strong acid.
initial mmoles of weak base, nb =
2.00_0_3_
n = MV = (0.100 M)(20.0 mL)
mmol

point (a) 0.0 mL (weak base)
pH =
11.13_0__
Weak base solution, so [OH1–] = {Kbc}1/2Kb = Kw/Ka = 1.8e–5 [OH1–] = {(1.8e–5)(0.10)}1/2 = 1.3e–3 pOH = –log(1.3e–3) = 2.87; pH = 14.00 – 2.87 = 11.13

point (b) 10.0 mL (buffer)
pH =
9.25_0__
This is the midpoint of the titration, so pH = pKa = 9.25

point (c) 20.0 mL (equivalence point, weak acid)
pH =
5.28_0__
The equivalence point is a solution of the weak acid NH41+; [NH41+] = 2.00 mmol/40.0 mL and Ka = 5.6e–10; [H3O1+] = {Ka[NH41+]}1/2 = 5.3e–6 M; pH = –log(5.3e–6)

point (d) 30.0 mL (strong acid)
pH =
1.699_0.001__
na = (0.100 M)(30.0 mL) = 3.00 mmol; xs mmols of acid = 3.00 initial – 2.00 react with base = 1.00 mmol; Vtotal = 20.0 + 30.0 = 50.0 mL; [H3O1+]= 1.00 mmol/50.0 mL = 0.0200 M; pH = –log(0.0200)

Making Buffers by Reaction
7.3-21. Three Ways to Make Buffers
We have now seen three ways in which buffers can be made:-
1mixing the acid and its conjugate base directly in the appropriate ratio to achieve the required pH
-
2adding a strong acid to an excess of weak base until the required pH is achieved
-
3adding a strong base to an excess of weak acid until the required pH is achieved
7.3-22. Preparing a Buffer with a Strong Acid and a Weak Base
Exercise 7.15:
How many mL of 0.26 M HCl must be added to 500. mL of 0.12 M NH3 to make a pH = 10.00 buffer?
First, construct the reaction table using x for the number of mmols of H3O1+ that are required.
Answer the following questions about the pH = 10.00 solution to obtain the volume of acid that would be needed.
pKa (Acid-Base Table with pKa)
mmol NH3 in initial solution
mmol NH41+ (in terms of x) in equilibrium mixture
mmol NH3 (in terms of x) in equilibrium mixture
Use the ratio and mmols to solve for x.
volume of 0.26 M HCl required
9.25_0__
The pKa of the ammonium ion is given in the acid-base table as 9.25

mmol NH3 in initial solution
60_0_2_
(0.12 M)(500. mL) = 60. mmol

log
 |
| mmol NH3 |
| mmol NH41+ |
 |
0.75_0__
Use the given pH and the acid pKa in the Henderson-Hasselbalch equation to obtain the ratio.

log
= pH − pKa = 10.00 − 9.25 = 0.75
 |
| mmol NH3 |
| mmol NH41+ |
 |
| mmol NH3 |
| mmol NH41+ |
5.6_0__
ratio = 10log ratio = 100.75 = 5.6 mol base/mol acid

mmol NH41+ (in terms of x) in equilibrium mixture
o_x_s
Reacting "x" mmol H3O1+ produces "x" mmol NH41+.

mmol NH3 (in terms of x) in equilibrium mixture
o_60.-x_s
60 mmols of NH3 initially – x mmol react = 60.–x mmol NH3

Use the ratio and mmols to solve for x.
9.1_0__
=
= 5.6 mmol base/mmol acid
Multiply both sides by x to get x out of denominator:
Solve for x:
| mmol NH3 |
| mmol NH41+ |
| (60 − x) mmol base |
| x mmol acid |
Multiply both sides by x to get x out of denominator:
60 − x = 5.6x
Solve for x:
x =
= 9.1 mmol acid
mmol H3O1+
| 60 |
| 6.6 |
volume of 0.26 M HCl required
35_0__

V = 9.1 mmol
= 35 mL
mL
| 1 mL |
| 0.26 mmol |
7.4 Acid-Base Composition from Equilibrium pH
Introduction
Solutions are frequently prepared by adjusting the solution pH to a desired level rather than adding a known volume of acid or base. For example, the easiest way to make a buffer of a desired pH is to decide on the proper acid-base pair, make a solution that contains an appreciable amount of the acid or base and then add a strong base or acid until the solution has the required pH. The question then becomes: Once you have attained the appropriate pH, what are the concentrations of the acid(s) and base(s) in the solution? We answer that question in this section.7.4-1. Method
One equation is required for each unknown concentration in a solution, so determining [H2X], [HX1–], and [X2–] in a solution of a diprotic acid involves three equations and three unknowns. The equilibrium constant expressions for K1 and K2 are two of the equations. The third equation is mass balance, which is based on the fact that even though reaction may take place in solution, the total amount of X does not change; i.e., co = [H2X] + [HX1–] + [X2–]. Fortunately, chemistry can often be used to simplify the algebra because only one or two of the concentrations are usually appreciable at any pH. Once the one or two appreciable concentrations have been determined at a given pH, the other concentrations can be readily determined from the given K values, co, and pH. Thus, our first task is to identify these one or two species that dominate the concentration. We do so by assuming that the concentration of a substance is negligible if it is less than 1% of the concentration of either its conjugate acid or base, so-
•the acid concentration is negligible if [base]/[acid] > 100, and
-
•the base concentration is negligible if [base]/[acid] < 0.01
-
•the acid is negligible if pH > pKa + log(100) = pKa + 2
-
•the base is negligible if pH < pKa + log(0.01) = pKa – 2
The concentration of an acid and its conjugate base are both appreciable at pH's within 2 pH units of the pKa of the acid, but only the acid can be appreciable below this pH range, and only the base can be appreciable above it.
7.4-2. Concentrations vs. pH
Monoprotic Acid: The concentrations of CH3COOH and CH3COO1– as a function of pH are shown in Figure 7.3. The pKa of CH3COOH is 4.7, so [CH3COOH] = co if pH < 2.7 (pH = 4.7 – 2), but [CH3COO1–] = co if pH > 6.7 (4.7 + 2). At intermediate pH values (2.7 < pH < 6.7), neither concentration is negligible, so we use [CH3COOH] + [CH3COO1–] = co. Thus, the solution is treated as a buffer in the yellow region of the figure, as an acetic acid solution at lower pH, and as an acetate ion solution at higher pH.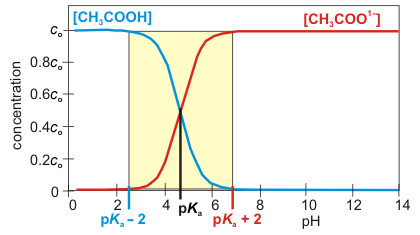
Figure 7.3: Concentrations of acetic acid and acetate ion as a function of pH.
The [acid] ~ co and [base] ~ 0 at pH's below (pKa – 2), but [acid] ~ 0 and [base] ~ co at pH's above (pKa + 2). The concentrations of both substances are appreciable only in the yellow region. pKa = 4.74

Figure 7.4: Concentrations of hydrosulfuric acid, hydrogen sulfide ion, and sulfide ion as a function of pH.
The concentrations of two substances are comparable and appreciable in the yellow boxes, but only one component is appreciable outside. The pH ranges of the yellow boxes are from pH = pKa – 2 to pH = pKa + 2.
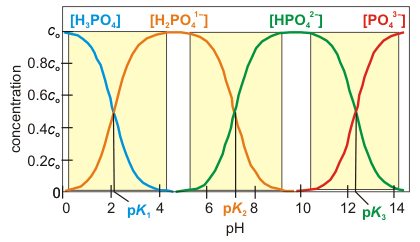
7.4-3. Triprotic Exercise
Exercise 7.16:








Solid NaOH is dissolved in a 0.10 M H3PO4 solution. Assume no volume change and calculate the concentrations of the phosphorus containing species at each pH. Use the Acid-Base Table with pKa to get the pKa's.
|
pK1 =
2.12_0__
The pKa of H3PO4.
|
pK2 =
7.21_0__
The pKa of H2PO41–.
|
pK3 =
12.32_0__
The pKa of HPO41–.
|
pH = 7.00
The number of appreciable concentrations is
2_0__
pH = 7 falls within a yellow box.

[H2PO41−]
=
0.062_0__
Use [H3O1+] = 1.0e–7 M and [HPO42–] + [H2PO41–] = co in the K2 expression.
M
[HPO42−]
=
0.038_0__
[H2PO41–] + [HPO42–] = co
M
[H3PO4]
=
8.3e-7_0__
Use [H2PO41–] = 0.062 M and [H3O1+] = 1.0e–7 M in the K1 expression.
M
[PO43−]
=
1.8e-7_0__
Use [HPO42–] = 0.038 M and [H3O1+] = 1.0e–7 M in the K3 expression.
M
pH = 10.00
The number of appreciable concentrations is
1_0__
pH = 10 is not within a yellow box.

[HPO41−]
=
0.10_0__
Only HPO42– is appreciable at pH = 10, so [HPO42–] = co at this pH.
M
[PO43−]
=
4.8e-4_0__
Use [H3O1+] = 1.0e–10 M and [HPO42–] = 0.10 M in the K3 expression.
M
[H2PO41−]
=
1.6e-4_0__
Use [HPO42–] = 0.10 M and [H3O1+] = 1.0e–10 M in the K2 expression.
M
[H3PO4]
=
2.1e-12_0__
Use [H2PO42–] = 1.6e–4 M and [H3O1+] = 1.0e–10 M in the K1 expression.
M
7.4-4. Combining Equilibria
While the protons of a polyprotic acid are removed individually, the equilibria can be combined to eliminate concentrations of intermediate ions. For example, consider the dissociation equilibria of H2S.H2S + H2O ⇌ HS1− + H3O1+ K1 = 1.0 × 10−7
HS1− + H2O ⇌ S2− + H3O1+ K2 = 1.3 × 10−13
H2S + 2H2O ⇌ S2− + 2H3O1+ K12 =
= K1K2 = 1.3 × 10−20
| [S2−][H3O1+]2 |
| [H2S] |
-
•The above K12 expression is best used for solutions in which pH < 5, because above this pH, the H2S concentration is no longer equal to the makeup concentration and would have to be determined with K1.
7.4-5. Exercise
Exercise 7.17:

Sulfide ion is used to selectively precipitate metal ions from solution, but the concentration of the sulfide ion must be adjusted carefully to select which metals will precipitate. This is done by adjusting the pH of the solution.
(a) What is [S2–] in a saturated solution of H2S (0.10 M) at a pH = 3.00?
[S2−]
=
1.3e-15_0__
Use [H2S] = 0.10 M and [H3O1+] = 1.0e–3 M in the K12 expression of the preceding section.
M
(b) At what pH will the sulfide ion concentration be 1.0 × 10–12 M?
pH =
4.44_0__
Use [H2S] = 0.10 M and [S2–] = 1.0e–12 M in the K12 expression of the preceding page. Don't forget that [H3O1+] is squared in the expression.

7.5 Acid-Base Indicators
Introduction
Acid-base indicators change color in small ranges of pH change and indicate the endpoint of an acid-base titration, but they too are weak acids and bases.7.5-1. Acid-Base Indicators
Acid-base indicators are organic dyes that are also weak acids. They function because the weak acid (HIn) and its conjugate base (In1–) differ in color. Consider the Ka reaction of the indicator HIn.HIn + H2O ⇌ + In1− + H3O1+
| Indicator | pH Range | Color Change |
|---|---|---|
| Methyl violet | 0.0–1.6 | yellow → blue |
| Thymol blue | 1.2–2.8 | red → yellow |
| Methyl orange | 3.2–4.4 | red → yellow |
| Bromocresol green | 3.8–5.4 | yellow → blue |
| Alizarin | 5.4–6.6 | colorless → yellow |
| Bromothymol blue | 6.0–7.6 | yellow → blue |
| Phenolphthalein | 8.2–10.0 | colorless → pink |
| Alizarin yellow R | 10.1–12.0 | yellow → red |
Table 7.2: Some Common Indicators The pH range and color change of selected acid-base indicators.
7.5-2. Titration Exercise
Exercise 7.18:

The titration of 25.00 mL of a weak monoprotic acid HA requires 35.22 mL of 0.1095 M NaOH to reach the equivalence point. The pH of the solution was 5.26 after the addition of 20.00 mL of the base.
What is the concentration of HA in the original solution?
base added at the equivalence point =
3.857_0__
nb = MV = (0.1095 M)(35.22 mL)
mmol

HA in the original HA solution =
3.857_0__
na = nb at the equivalence point
mmol

[HA]
=
0.1543_0__
[HA] = 3.857 mmol/25.00 mL
M
What is the pKa of the acid?
A1– present at the 20.00 mL point of the titration =
2.190_0_4_
nb = MV = (0.1095 M)(20.00 mL)
mmol

HA present at the 20.00 mL point of the titration =
1.667_0__
3.857 mmol initial – 2.190 react with base
mmol

if the pH at this point is 5.26, the pKa =
5.14_0__
it is a buffer solution, so pH = pKa + log(nb/na)

What is the pH at the equivalence point?
the concentration of A1– at the equivalence point is [A1–] =
0.06405_0__
[A1–] = 3.857 mmol/(25.00 + 35.22) mL

the pKb of A1– is pKb =
8.86_0__
pKb = 14.00 – pKa

the Kb of A1– is Kb =
1.4e-9_2e-11__
Kb = 10–pKb

the concentration of hydroxide at the equivalence point is [OH1–] =
9.4e-6_.1e-6__

[OH1−] =
M
 | Kb[A1−] |
the pH at the equivalence point is pH =
8.97_0.01__
pH = 14.00 – pOH = 14.00 + log[OH1–]

What indicator in Table 7.2 would be best to use for this titration? (Enter the first four letters.)
o_phen_ins
Only one indicator in the table has a pKa of about 9 or a pH range of 8–10.