Chapter 8 – Equilibria Containing Metal Ions

Introduction

Several different equilibria must be considered when dealing with aqueous metal ions:

•
Metal ions are Lewis acids, so they are involved in acid-base equilibria.
•
As Lewis acids, they can react with other Lewis bases to form complex ions.
•
Many metal ions form sparingly soluble salts, so solubility equilibria must also be considered.

In this chapter, all three of these types of equilibria are considered.

8.1 Acid-Base Equilibria

Introduction

While metal ions rarely have protons to donate as required by the Brønsted acid definition, they can accept electron pairs to form covalent bonds, which makes them acidic by the Lewis definition. Thus, an aqueous solution of iron(III) nitrate is acidic even though it contains no protons.

Objectives

•
Explain the acidity of metal ions and write the acid-dissociation reaction associated with the acidity.

8.1-1. Metal Ions as Acids

Metal ions form acidic solutions because the positive charge on the metal ion weakens the O–H bonds of the bound water molecules.

Fe(NO₃)₃ is a strong electrolyte that dissociates completely into Fe³⁺ and NO₃^1– ions. The small, highly charged iron(III) ion interacts with the surrounding water molecules in a Lewis acid-base reaction to produce Fe(H₂O)₆³⁺, the octahedral ion in Figure 8.1. Ions, such as Fe(H₂O)₆³⁺, that consist of a metal ion bound to several molecules or anions are called complex ions, and the bound molecules or anions are referred to as ligands. The positive charge of the central metal ion withdraws electron density from the O–H bonds, which weakens them and makes the water ligands stronger acids.

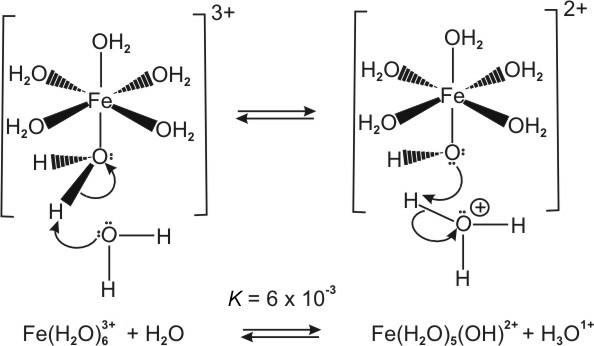
Figure 8.1: Acidity of Metal Ions

Thus, the acidity of Fe³⁺ ions arises from the following reaction:

Fe(H₂O)₆³⁺ + H₂O ⇌ [Fe(H₂O)₅OH]²⁺ + H₃O¹⁺ K = 6e-03

which is the reaction of a weak acid with water, so the equilibrium constant is the K_a of the weak acid Fe(H₂O)₆³⁺. Note that Fe(H₂O)₆³⁺ is a stronger acid than acetic acid (K_a = 1.8e–05). The K_a values of several hydrated metal ions are listed in the table.

Hydrated Metal Ion	K_a
Fe(H₂O)₆³⁺	6e–03
Al(H₂O)₆³⁺	1e–05
Cu(H₂O)₆²⁺	3e–08
Zn(H₂O)₆²⁺	1e–09
Ni(H₂O)₆²⁺	1e–10

Table 8.1: Acid Dissociation Constants of Hydrated Metal Ions

8.2 Dissolution and the Solubility Product Constant

Introduction

Calcium carbonate (also known as limestone) is a slightly soluble salt that is responsible for scale in containers of hard water. In addition, caves and the unusual structures in them called stalactites and stalagmites are the result of dissociation and subsequent precipitation of calcium carbonate. This important dissociation process is represented in the following equilibrium:

CaCO₃(s) ⇌ Ca²⁺(aq) + CO₃^2–(aq) K = [Ca²⁺][CO₃^2–]

This type of process, the equilibrium between a solid and its ions in solution, is an important one and forms the topic of this section.

Objectives

•
Write the dissociation reaction of a slightly soluble salt.
•
Write the expression for the solubility product constant, K_sp, of a given salt.
•
Calculate the solubility of an ionic compound given its K_sp value, and vice versa.
•
Calculate the solubility of an ionic compound in the presence of one of its ions.

8.2-1. The Solubility Product

The equilibrium between a solid and its solution is an important one. Indeed, it is so important that the equilibrium is given a special symbol and name: the solubility product constant (K_sp). Consider the equilibrium between solid silver chloride and its solution:

AgCl ⇌ Ag¹⁺ + Cl¹⁻.

The activity of the solid is unity, so the form of the equilibrium constant, K_sp, for the reaction is

K_sp = [Ag¹⁺][Cl¹⁻].

It is called the solubility product constant because it is simply a product of concentrations that indicates the solubility of the solid. Most slightly soluble salts contain basic anions, which are involved in both acid-base equilibria with water and salt dissolution equilibria with metal ions. This can lead to a complicated set of equilibria in the case of fairly strong bases such as CO₃^2– and PO₄^3–. Consequently, our discussions of solubility in water centers on the solubility of neutral or only weakly basic anions, such as Cl^1– and SO₄^2–. The reaction table for the dissociation of Ag₂SO₄ in water has the following form:

	Ag₂SO₄(s)	⇌	2 Ag¹⁺	+	SO₄^2–	K_sp = 1.4 × 10^–5
initial	enough		0		0	M
Δ			+2x		+x	M
equilibrium	some		2x		x	M

where x is the molar solubility of silver sulfate. The activity of a solid is unity, so it does not enter into the equilibrium constant expression. Consequently, the amount of solid is irrelevant so long as there is enough of the solid initially to assure that there is some solid present at equilibrium. The K_sp expression is

K_sp = 1.4 × 10⁻⁵ = [Ag¹⁺]²[SO₄²⁻] = (2x)²(x) = 4x³

Solving the above expression for x, we obtain the molar solubility of silver sulfate and the ion concentrations in a saturated solution in terms of the solubility product constant.

x =

K_sp

= [SO₄²⁻] =

[Ag¹⁺]

Substituting 1.4 × 10^–5 = K_sp, we obtain the following:

•
molar solubility of silver sulfate; x = 0.015 M
•
[SO₄^2–] = x = 0.015 M
•
[Ag¹⁺] = 2x = 0.030 M

We can check our calculation by substituting concentrations back into the K_sp expression:

K_sp = [Ag¹⁺]²[SO₄²⁻] = (0.030)²(0.015) = 1.4e−05

K_sp values can be found in Selected Solubility Product Constants in the Resources.

8.2-2. K_sp from Solubility Exercise

Exercise 8.1:

What is the K_sp of MgF₂ (M_m = 62.3 g/mol) if its solubility is 7.6 mg/100. mL?

The molar solubility of MgF₂ =

1.2e-3_0__ 7.6 mg/100. mL = 76 mg/1 L = 0.076 g/L

0.076 g MgF₂

1 L solution

1 mol MgF₂

62.3 g MgF₂

1.2e−03 mol MgF₂

1 L solution

= 1.2e−03 M

[Mg²⁺] =

1.2e-3_0__ There is one mole of Mg for each mole of MgF₂, so
[Mg²⁺] = x = 1.2e–03 M. M

[F^1–] =

2.4e-3_0__ There are two moles of F for each mole of MgF₂, so
[F^1–] = 2x = 2(1.2e–03) = 2.4e–03 M. M

K =

7.3e-9_0__ Carry along extra significant figures to reduce rounding errors:
[Mg²⁺][F^1–]² = (1.22e–03)×(2.44e–03)² = 7.3e–09.

8.2-3. K_sp from pH Exercise

Exercise 8.2:

What is the K_sp of Fe(OH)₂ if the pH of a saturated solution is 9.07? Watch out for rounding errors!

[OH^1–] =

1.2e-5_0__

pOH	=	14.00 − pH
	=	14.00 – 9.07
	= 4.93;

[OH¹⁻]	=	10^–4.93
	=	1.2e–05 M

[Fe²⁺] =

5.9e-6_0__ Watch out for rounding errors! There are two moles of OH^1– for every on mole of Fe²⁺, so [Fe²⁺] = [OH^1–]/2 = 5.9e–06 M. M

K =

8.1e-16_0__ Carry along extra significant figures to reduce rounding errors:
[Fe²⁺][OH^1–]² = (5.874e–06)×(1.175e–05)² = 8.1e–16

8.2-4. Solubility from K_sp Exercise

Exercise 8.3:

The K_sp of AgI is 8.3e–17. What is its molar solubility?

Molar solubility =

9.1e-9_0__ K_sp = [Ag¹⁺][I^1–] = x², so x = K_sp^1/2 M

8.2-5. K_sp and Strong Bases

Let us now determine the solubility of the salt of Ag₃PO₄; K_sp = 2.6 × 10^–18. The reaction table for the dissolution has the following form:

	Ag₃PO₄(s)	⇌	3 Ag¹⁺	+	PO₄^3–
initial	enough		0		0
Δ			+3x		+x
equilibrium	some		3x		x

K_sp = [Ag¹⁺]³[PO₄^3–] = (3x)³(x) = 27x⁴

Solving 27x⁴ = 2.6 × 10^–18 for x, we obtain a solubility of 1.8 × 10^–5 M. However, the measured solubility is 1.5 × 10^–4. Thus, the actual solubility is over eight times greater than that determined with K_sp. The K_sp is correct, and it is still obeyed. However, PO₄^3– is a fairly strong base, so some of the PO₄^3– that is produced by the dissolution reacts with water to produce HPO₄^2– and OH^1–. Therefore,

K_sp = [Ag¹⁺]³[PO₄³⁻]

is still valid, but the loss of PO₄^3– in the reaction with water means that the equality

3[Ag¹⁺] = [PO₄^3–]

is no longer valid. This is why we restrict our discussion of solubility to neutral or weakly basic salts only. We treat the solubility of Ag₃PO₄ in more detail in Section 8.4.

8.2-6. Cation:Anion Ratios in K_sp

The preceding examples demonstrate that the form of the K_sp expression in terms of the molar solubility of the salt (x) depends only upon the cation:anion ratio in the salt. The K_sp expressions for the common ratios are given below.

Cation:Anion Ratio	K_sp
1:1	x²
1:2 or 2:1	4x³
1:3 or 3:1	27x⁴
2:3 or 3:2	108x⁵

Table 8.2: K_sp expressions in terms of molar solubilities (x) for salts with common cation:anion ratios

The relative solubilities of salts with the same cation:anion ratios can be obtained by simply looking at the magnitudes of their K_sp's. However, when the ratios are different, you must determine the value of x.

8.2-7. Determining Relative Solubilities Exercise

Exercise 8.4:

List the following salts in order of increasing solubility.

PbCl₂	K_sp = 1.7e–5
AgCl	K_sp = 1.2e–10
TlCl	K_sp = 1.9e–4

Least soluble salt:

PbCl₂
AgCl: x = (1.2e−10)^1/2
~ 1e−5 M
AgCl
TlCl
AgCl: x = (1.2e−10)^1/2
~ 1e−5 M

Intermediate salt:

PbCl₂
TlCl: x = (1.9e−4)^1/2
= 0.014 M
AgCl
TlCl: x = (1.9e−4)^1/2
= 0.014 M
TlCl

Most soluble salt:

PbCl₂
AgCl
PbCl₂: x = (1.7e−5)^1/3
= 0.016 M
TlCl
PbCl₂: x = (1.7e−5)^1/3
= 0.016 M

8.2-8. Predicting the More Soluble Salt Exercise

Exercise 8.5:

Indicate the more soluble compound in each pair.

PbSO₄ (K_sp = 2e–8) The ion ratios are the same, so the more soluble compound is the one with the higher K_sp.
CaSO₄ (K_sp = 2e–5)

BaF₂ (K_sp = 2e–6)
PbF₂ (K_sp = 4e–8) The ion ratios are the same, so the more soluble compound is the one with the higher K_sp.

BaCrO₄ (K_sp = 2e–10) The ion ratios are NOT the same, so the solubilities must be determined. BaCrO₄ is
x²
and Ag₂CrO₄ is
4x³.
Ag₂CrO₄ (K_sp = 3e–12)

Ag₃PO₄ (K_sp = 2e–18)
Mg₃(PO₄)₂ (K_sp = 5e–24) The ion ratios are NOT the same, so the solubilities must be determined. Ag₃PO₄ is
27x⁴
and Mg₃(PO₄)₂ is
108x⁵.

8.2-9. Common-Ion Effect

Consider the dissolution of Ag₂SO₄(s) in 1.0 M Na₂SO₄.

	Ag₂SO₄(s)	⇌	2 Ag¹⁺	+	SO₄^2–	K_sp = 1.4 × 10^–5
initial	enough		0		1.0	M
Δ			+2x		+x	M
equilibrium	some		2x		0.10 + x	M

K_sp = [Ag¹⁺]²[SO₄^2–] = (2x)²(1.0 + x)

which would involve solving a cubic equation. However, in the beginning of this section, we determined that the solubility of Ag₂SO₄ in water was 0.015 M, and the presence of the common ion (sulfate) will decrease the dissociation, so

x < 0.015 M.

If we assume that x is negligible in the addition

(1.0 + x ~ 1.0),

we can simplify the expression

K_sp = (2x)²(1.0)

which is solved for x as follows:

x =

K_sp

4(1.0)

1.4 × 10⁻⁵

4.0

= 1.9 × 10⁻³ M

Thus, the solubility drops from 0.015 M in water down to 0.0019 M (an 88% drop) in 1.0 M Na₂SO₄ due to the presence of the common ion.

8.2-10. Common-Ion Solubility from pH Exercise

Exercise 8.6:

Determine the solubility of Sn(OH)₂ in solutions buffered at the following pHs.

K_sp =

1.4e-28_0__ The solubility product constant can be found in Selected Solubility Product Constants.

pH = 9.00

The concentration of the common ion: [OH^1–] = 1.0e-5_0_2_ pOH = 14.00 – 9.00 = 5.00; [OH^1–] = 10^–pOH = 1.0e–5 M

solubility 1.4e-18_0__

[Sn²⁺] =

K_sp

[OH¹⁻]²

1.4e−28

(1.0e−05)²

= 1.4e−18 M

pH = 2.00

The concentration of the common ion: [OH^1–] = 1.0e-12_0_2_ pOH = 14.00 - 2.00 = 12.00; [OH^1–] = 1.0e–12 M

solubility 1.4e-4_0__

[Sn²⁺] =

K_sp

[OH¹⁻]²

1.4e−28

(1.0e−12)²

= 1.4e−04 M

8.2-11. Solubility of AgCl Exercise

Exercise 8.7:

K_sp = 1.8e–10 for AgCl. Determine the solubility of AgCl in the following:

water

solubility = 1.3e-5_0__

a 1:1 salt, so x	=	K_sp^1/2
	=	(1.8e–10)^1.2
	=	1.3e–05 M

0.10 M NaCl

solubility = 1.8e-9_0__ [Cl^1–] = 0.10 M, so

[Ag¹⁺] =

K_sp

[Cl¹⁻]

1.8e−10

0.10

= 1.8e−09 M

8.3 Precipitation and Separation of Ions

Introduction

Our discussions thus far have focused on the amount of a slightly soluble salt that dissolves, but now we consider the reverse process; i.e., does a precipitate form under a given set of concentrations? We do this by considering the dissociation reaction from the reverse direction; that is, we examine the formation (precipitation) of the salt.

Objectives

•
Predict whether a precipitation will occur given the concentrations of the ions and the K_sp of the salt.
•
Determine the appropriate anion concentration to achieve maximum separation of two ions by the selective precipitation of one.

8.3-1. The Ion Product

Does a solid form under a given set of conditions, or what minimum concentration of one of the ions is required to produce a precipitate? These are two questions we will answer in this section. For example, consider a mixture that contains some solid Ag₂SO₄(s) suspended in a solution that is 0.01 M in Ag¹⁺ and 0.10 M in [SO₄^2–]. Under these conditions, does the solid dissolve or does it precipitate out of solution? To answer this question, we examine the direction in which the following reaction is proceeding under these conditions.

	Ag₂SO₄(s)	⇌	2 Ag¹⁺	+	SO₄^2–	K_sp = 1.4 × 10^–5
initial	?		0.01		0.10	M

The direction in which a reaction proceeds depends upon the relative values of the reaction quotient, Q, and the equilibrium constant K. The reaction quotient for dissociation is used so frequently that it is given a special name and symbol: the ion product, Q_ip.

•
Precipitation occurs (reaction proceeds ←) if Q_ip > K_sp
•
The salt dissolves (reaction proceeds →) if Q_ip < K_sp

In this case, Q_ip = [Ag¹⁺]²[SO₄^1–] = (0.01)²(0.10) = 1 × 10^–5 and K_sp = 1.4 × 10^–5. K_sp > Q_ip, so some salt can still dissolve and no precipitate would form.

8.3-2. Identifying Precipitating Hydroxides Exercise

8.3-3. Identifying Precipitating Chlorides Exercise

Exercise 8.9:

Identify any precipitates that result when 5.0 mL of 0.010 M HCl is added to 20. mL of a solution in which [Tl¹⁺] = 0.15 M and [Pb²⁺] = 0.20 M.

K_sp of TlCl = 1.9e–4

K_sp of PbCl₂ = 1.7e–5

Concentrations after mixing:
[Cl1^1–] =

2.0e-3_0_2_ [Cl^1–] = 0.05 mmol/25 mL M

[Tl¹⁺] =

0.12_0__ [Tl¹⁺] = 3.0 mmol in 25 mL M

[Pb²⁺] =

0.16_0__ [Pb²⁺] = 4.0 mmol in 25 mL M

Ion-products:

TlCl: 2.4e-4_0__ (0.12)(0.0020)

PbCl₂: 6.4e-7_0__ (0.16)(0.0020)²

The precipitate is _______________.

TlCl
PbCl₂ Q_ip > K_sp for TlCl but not for PbCl₂

8.3-4. Determining a Required Concentration

Precipitation occurs when the ion-product exceeds the solubility product, so the concentration of one reactant that is required to initiate precipitation can be determined if the concentration of the other reactant and the K_sp are known. To determine the minimum concentration required, we solve the K_sp expression for the unknown concentration, which is the maximum concentration at which no precipitation occurs. Thus, the calculation indicates both the minimum concentration required for precipitation or the maximum concentration allowed with no precipitation.

8.3-5. Determining pH at which Precipitate Forms Exercise

Exercise 8.10:

At what pH does Mg(OH)₂ (K_sp = 1.8 × 10^–11) begin to precipitate from a solution that is 0.01 M in Mg²⁺?

Use the given Mg²⁺ concentration to determine the hydroxide ion concentration at which Q_ip = K_sp.

[OH^1–] = 4e-5_0__

K_sp = [Mg²⁺][OH¹⁻]²

[OH¹⁻] =

K_sp

[Mg²⁺]

1.8 × 10⁻¹¹

0.01

= 4 × 10⁻⁵ M

Convert the hydroxide ion concentration into a pOH.

pOH = 4.4_0__ pOH = –log(4e–5) = 4.4

Convert the pOH into a pH.

pH = 9.6_0__ pH = 14.0 – 4.4 = 9.6
Precipitation occurs at pH values above 9.6, but not below.

8.3-6. Separations

Chemists frequently need to separate a mixture into its components. In the case of aqueous mixtures of ions, this can often be accomplished by selectively precipitating the ions from the solution. We demonstrate the method by separating Sn²⁺ and Mg²⁺ ions from a solution by selectively precipitating the less soluble hydroxide by adjusting the pH to a value that results in the precipitation of only one ion. The K_sp of Sn(OH)₂ is much less that that of Mg(OH)₂, so we will choose to precipitate Sn(OH)₂ and leave Mg²⁺ ions in solution. We could determine the pH at which Sn(OH)₂ begins to precipitate, and adjust the pH to a slightly higher value to precipitate Sn(OH)₂. However, Sn²⁺ ions will remain in solution with the following concentration:

[Sn²⁺] =

K_sp

[OH¹⁻]²

In an optimum separation, the remaining Sn²⁺ concentration in solution should be at a minimum. To minimize the Sn²⁺ concentration, the hydroxide ion concentration should be as high as possible without precipitating any Mg²⁺ ions. Thus, we determine the hydroxide ion concentration at which Mg(OH)₂ begins to precipitate and adjust the pH of the solution to just below that value. See the example in Exercise 8.11.

8.3-7. Optimum Separation Exercise

Exercise 8.11:

A solution is 0.010 M each in Sn²⁺ and Fe²⁺. At what pH would optimum separation be achieved?
K_sp = 8.0e–16 for Fe(OH)₂ and 1.4e–28 for Sn(OH)₂.

Which metal ion should be precipitated?

Sn²⁺
Fe²⁺ The hydroxide with the lowest K_sp will precipitate first.

Which of the following would be the best pH to use for the separation?

6 Determine the hydroxide ion concentration that would be required to precipitate the more soluble hydroxide:

[OH¹⁻] =
K_sp
[Fe²⁺]

=
8 × 10⁻¹⁶
0.01

= 3 × 10⁻⁷ M

pOH = 6.5; pH = 7.5
Fe(OH)₂ begins to precipitate at pH = 7.5. For best separation, the pH should be as high as possible to precipitate as much Sn(OH)₂ as possible, but it must be below
pH = 7.5
to avoid precipitating Fe(OH)₂. Thus,
pH = 7
is the optimum pH in the selection.
7
8 Determine the hydroxide ion concentration that would be required to precipitate the more soluble hydroxide:

[OH¹⁻] =
K_sp
[Fe²⁺]

=
8 × 10⁻¹⁶
0.01

= 3 × 10⁻⁷ M

pOH = 6.5; pH = 7.5
Fe(OH)₂ begins to precipitate at pH = 7.5. For best separation, the pH should be as high as possible to precipitate as much Sn(OH)₂ as possible, but it must be below
pH = 7.5
to avoid precipitating Fe(OH)₂. Thus,
pH = 7
is the optimum pH in the selection.
9 Determine the hydroxide ion concentration that would be required to precipitate the more soluble hydroxide:

[OH¹⁻] =
K_sp
[Fe²⁺]

=
8 × 10⁻¹⁶
0.01

= 3 × 10⁻⁷ M

pOH = 6.5; pH = 7.5
Fe(OH)₂ begins to precipitate at pH = 7.5. For best separation, the pH should be as high as possible to precipitate as much Sn(OH)₂ as possible, but it must be below
pH = 7.5
to avoid precipitating Fe(OH)₂. Thus,
pH = 7
is the optimum pH in the selection.
10 Determine the hydroxide ion concentration that would be required to precipitate the more soluble hydroxide:

[OH¹⁻] =
K_sp
[Fe²⁺]

=
8 × 10⁻¹⁶
0.01

= 3 × 10⁻⁷ M

pOH = 6.5; pH = 7.5
Fe(OH)₂ begins to precipitate at pH = 7.5. For best separation, the pH should be as high as possible to precipitate as much Sn(OH)₂ as possible, but it must be below
pH = 7.5
to avoid precipitating Fe(OH)₂. Thus,
pH = 7
is the optimum pH in the selection.
11 Determine the hydroxide ion concentration that would be required to precipitate the more soluble hydroxide:

[OH¹⁻] =
K_sp
[Fe²⁺]

=
8 × 10⁻¹⁶
0.01

= 3 × 10⁻⁷ M

pOH = 6.5; pH = 7.5
Fe(OH)₂ begins to precipitate at pH = 7.5. For best separation, the pH should be as high as possible to precipitate as much Sn(OH)₂ as possible, but it must be below
pH = 7.5
to avoid precipitating Fe(OH)₂. Thus,
pH = 7
is the optimum pH in the selection.

What are the concentrations of the metal ions in solution after precipitation?

[Fe²⁺] =

0.01_0__ Fe(OH)₂ does not precipitate at pH = 7, so [Fe²⁺] = 0.01 M M

[Sn²⁺] =

1e-14_0__ Use pH = 7 to determine that

[OH¹⁻] = 1e–07 M,

which is then used in the K_sp expression for Sn(OH)₂,

[Sn²⁺] =

1e−28

(1e−07)²

= 1e−14 M.

Note that the precipitated hydroxide could be redissolved in an acidic solution, so the solution of two metal ions could be separated into two solutions that each contain only one metal ion.

8.3-8. Reaction Table Exercise

Exercise: 8.12

Determine the mass of Ag₂CrO₄ (K_sp = 1.1e–12, M_m = 331.7 g/mol) that is formed and the concentrations of Ag¹⁺ and CrO₄^2– in the resulting solution when 50. mL of 0.10 M K₂CrO₄ and 50. mL of 0.10 M AgNO₃ are mixed.

The equilibrium constant for the precipitation is ~1e+12 (the reciprocal of K_sp because the reaction is the reverse of the dissociation reaction), so essentially all of the limiting reactant disappears.

Fill in the reaction table in millimoles.

2 Ag¹⁺

CrO₄^2–

⇌

Ag₂CrO₄(s)

initial

5.0_0__

50. mL solution ×

0.10 mmol Ag¹⁺

mL solution

= 5.0 mmol Ag¹⁺

5.0_0__

50. mL solution ×

0.10 mmol CrO₄^2–

mL solution

= 5.0 mmol CrO₄^2–

0_0__ There is none initially.

mmol

-5.0_0__ All of the limiting reactant disappears.

-2.5_0__ Assume that all of the limiting reactant disappears.

o_+2.5_s Based on the amount of limiting reactant that disappears. Don't forget to include the sign of the change.

mmol

equilibrium

0_0__ Assume that all of the limiting reactant disappears.

2.5_0__ Sum the initial and Δ lines.

mmol

mass (in grams) of Ag₂CrO₄ that precipitates =

0.83_0__

2.5 mmol ×

332 mg

mmol

= 8.3e2 mg = 0.83 g

[CrO₄^2–] =

0.025_0__

[CrO₄^2–] =

2.5 mmol

100 mL

= 0.025 M

The stoichiometry of Chapter 1 can be used for all entries except the limiting reactant because the limiting reactant concentration cannot be zero if the K_sp is to be satisfied. Finding the concentration of the limiting reactant is the same as finding the solubility of the salt in the presence of a common ion (the excess reactant). Use the K_sp expression and the [CrO₄^2–] determined above to find the limiting reactant concentration, which will be small but not zero.

[Ag¹⁺] =

6.6e-6_0__

[Ag¹⁺] =

K_sp

[CrO₄^2–]

1.1 × 10⁻¹²

0.025

= 6.6 × 10⁻⁶ M

8.3-9. Reaction Table Exercise

Exercise 8.13:

What is the concentration of lead ions in a solution formed by mixing 24 mL of 0.10 M Pb(NO₃)₂ and 50. mL of 0.12 M KF?

Be sure to include coefficients with the substances in the balanced equation. (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a caret (^). For example, NH_4^1+ for NH₄¹⁺. Include any coefficients other than 1. Omit any spaces.)

	Cation		Anion		Product
	o_Pb^2+_s PbF₂ precipitates.	+	o_2F^1-_s PbF₂ precipitates.	→	o_PbF_2_s PbF₂ precipitates.
initial	2.4_0__ (24 mL)(0.10 M) = 2.4 mmol Pb²⁺		6.0_0_2_ (50 mL)(0.12 M) = 6.0 mmol F^1–		0_0__ There is no PbF₂ initially.	mmol
Δ	-2.4_0__ Pb²⁺ is the limiting reactant.		-4.8_0__ Pb²⁺ is the limiting reactant, and 2 mol F^1– are required for each 1 mol Pb²⁺.		o_+2.4_s Pb²⁺ is the limiting reactant, and one mole of PbF₂ forms for each mol of Pb²⁺ that reacts.	mmol
equilibrium	0_0__ Sum the initial and Δ lines: 2.4 − 2.4 = 0. All of the limiting reactant disappears.		1.2_0__ Sum the initial and Δ lines: 6.0 − 4.8 = 1.2 mmol F¹⁻		2.4_0__ Sum the initial and Δ lines: 0 + 2.4 = 2.4 mmol PbF₂	mmol

[F^1–] =

0.016_0__ [F^1–] = 1.2 mmol/74 mL = 0.016 M M

[Pb²⁺] =

1.4e-4_0__

[Pb²⁺] =

K_sp

[F¹⁻]²

3.7e−8

0.016²

= 1.4e−04 M

8.4 Complex Ions

Introduction

Complex ions are ions in which a central metal ion is surrounded by molecular or anionic ligands. For example, the [Fe(H₂O)₆]³⁺ ion discussed in Section 8.1 is a complex ion. The ligands and the metal are in equilibrium in much the same way that the protons and anion of a polyprotic acid are in equilibrium. That is, there is a series of equilibria in which the ligands are added or removed one at a time. However, in our treatment of complex-ion equilibria, we will consider only the overall process in which all of the ligands are added or removed in one step.

Objectives

•
Write the formation reaction for a given complex ion.
•
Write the formation constant expression for a given complex ion.

8.4-1. The Formation and Dissociation Constants

The equilibrium constant governing the one-step formation of a complex ion from its metal ion and ligands is called the formation constant, K_f. Table 8.3 contains the formation constants at 25 °C for some common complex ions.

Complex Ion	K_f	K_d
Ag(NH₃)₂¹⁺	1.7e07	5.9e–08
Ag(CN)₂^1–	3.0e20	3.3e–21
Cu(NH₃)₄²⁺	4.8e12	2.1e–13
Fe(CN)₆^4–	1.0e35	1.0e–35
Fe(CN)₆^3–	1.0e42	1.0e–42
Ni(NH₃)₆²⁺	5.6e08	1.8e–09
Zn(OH)₄^2–	2.8e15	3.6e–16

Table 8.3: Formation and Dissociation Constants at 25 °C

As an example, consider formation of the complex ion Ag(NH₃)₂¹⁺.

Ag¹⁺ + 2 NH³ ⇌ Ag(NH₃)₂¹⁺

The equilibrium constant for the reaction is the formation constant of the Ag(NH₃)₂¹⁺ ion.

K_f =

[Ag(NH₃)₂¹⁺]

[Ag¹⁺][NH₃]²

= 1.7 × 10⁷

Biochemists prefer the reverse of the formation reaction, so the dissociation constant, K_d, is also common. However, the K_d of an ion is merely the reciprocal of its K_f. Table 8.3 shows both the dissociation and formation constants of selected complex ions.

8.4-2. Exercise

Exercise 8.14:

What is the concentration of free Cu²⁺ in a 0.26 M solution of Cu(NH₃)₄²⁺ (K_d = 2.1 × 10^–13)?

Use x for the amount of Cu(NH₃)₄²⁺ that reacts and determine the equilibrium line for the reaction table.

	Cu(NH₃)₄²⁺	⇌	Cu²⁺	+	4 NH₃
equilibrium	o_0.26-x_ins Initial = 0.26; Δ = −x		o_x_ins Initial = 0; Δ = +x		o_4x_ins Initial = 0; Δ = +4x	M

Assume that x is negligible compared to the initial concentration of Cu(NH₃)₄²⁺ to set up the equilibrium constant expression and solve for x ([Cu²⁺]).

[Cu²⁺] = 7.3e-4_0__ If x is negligible in the subtraction, then

K_d =

[Cu²⁺][NH₃]⁴

Cu(NH₃)₄²⁺

(x)(4x)⁴

0.26

2.1e−13 =

256x⁵

0.26

So x = [Cu²⁺] = 7.3e–4 M M

8.4-3. Separations with Sulfide Ion

Metal sulfides are very insoluble, so many metals can be separated by adjusting the sulfide ion concentration in solution. Recall from Section 7.4 that the two K_a equilibria of H₂S can be combined to eliminate HS^1– ion as follows:

H₂S + 2 H₂O ⇌ S²⁻ + 2 H₃O¹⁺ K₁₂ =

[S²⁻][H₃O¹⁺]²

[H₂S]

= K₁K₂ = 1.3 × 10⁻²⁰

If [H₂S] is known, K₁₂ allows us to determine the pH required for a given [S^2–] or to determine [S^2–] from a given pH. H₂S is a gas, and its solubility in water at 25 °C is 0.10 M; thus, a solution with a desired sulfide ion concentration can be prepared by buffering a solution to a predetermined pH and then saturating it with H₂S. Both [H₂S] and pH are known, so the sulfide ion concentration can be determined. However, as was also shown in Section 7.4, above

pH = 5,

the H₂S concentration can no longer be assumed to be 0.10 M because the HS^1– concentration can no longer be ignored.

8.4-4. Sulfide Separation Exercise

Exercise 8.15:

To what pH should a solution that is 0.010 M in each Fe²⁺ and Mn²⁺ be saturated with H₂S to achieve an optimum separation of ions?

•
K_sp(MnS) = 5.6e–16
•
K_sp(FeS) = 6.3e–18

The optimum separation is accomplished at the highest pH that does not precipitate the more soluble sulfide, so first determine the highest [S^2–] allowed without precipitating the more soluble sulfide.

[S^2–] =

5.6e-14_0__ MnS has the higher K_sp, so it is more soluble. Determine the maximum sulfide from the K_sp and the given Mn²⁺ concentration.

[S²⁻] =

K_sp

[Mn²⁺]

5.6e−16

0.010

Use the K₁₂ expression in the previous section to determine the [H₃O¹⁺] required to deliver the above sulfide ion concentration.

[H₃O¹⁺] =

1.5e-4_0__ Use the [S^2–] determined above with the K₁₂ value and the fact that saturated H₂S is 0.10 M.

[H₃O¹⁺] =

K₁₂[H₂S]

[S²⁻]

(1.3e−20)(0.10)

5.6e−14

The optimum separation pH to the nearest 0.1 pH units is

pH =

3.8_0__ –log(1.5e–4) = 3.82, so the pH must be kept below 3.82. To the nearest 0.1, that is 3.8.

Assume the pH is adjusted to exactly the above pH; i.e., if the above answer is 4.2, assume a pH of 4.20 and calculate the ion concentrations at this pH.

[S^2–] =

5.2e-14_0__ Solve K₁₂ expression for [S^2–]. [H₃O¹⁺] = 10^–3.80 = 1.58e–4 M

[S²⁻] =

K₁₂[H₂S]

[H₃O¹⁺]²

(1.3e−20)(0.10)

(1.58e−4)²

= 5.2e−14

[Mn²⁺] =

0.010_0__ The sulfide concentration is below that required for precipitation of MnS. M

[Fe²⁺] =

1.2e-4_0__

[Fe²⁺] =

K_sp

[S²⁻]

6.3e−18

5.2e−14

= 1.2e−04

Is this a good separation?

Yes Over 1% of the Fe²⁺ ions remain in solution with the Mn²⁺. Such a large fraction is not considered a very good separation.
No

8.5 Competing or Simultaneous Equilibria

Introduction

As we have seen, metal ions can be involved in acid-base, solubility, and complex ion equilibria. Thus, several components of a solution containing a metal ion may compete with one another for the metal ion. These competing or simultaneous equilibria are the topic of this section.

Objectives

•
Calculate the solubility of a slightly soluble salt in the presence of a substance that forms a complex ion with the metal.
•
Write the reaction for the dissociation of a basic salt in acid.
•
Determine the equilibrium constant for the dissociation of a basic salt in acid.

8.5-1. Silver Chloride Dissolves in Ammonia

Ag¹⁺ ions react with both chloride ions and ammonia molecules, so two competing equilibria are established when AgCl is placed in an aqueous solution of NH₃ as both NH₃ and Cl^1– compete for Ag¹⁺.

( Reaction 1 )

AgCl(s) ⇌ Ag¹⁺ + Cl¹⁻ K_sp = 1.8 × 10⁻¹⁰

( Reaction 2 )

Ag¹⁺ + 2 NH₃ ⇌ Ag(NH₃)₂¹⁺ K_f = 1.7 × 10⁷

To determine how much AgCl would dissolve in NH₃, we add Reaction 1 and Reaction 2 to obtain Reaction 3, which represents the dissolution of AgCl in NH₃. The equilibrium constant for the reaction would then be the product of the equilibrium constants of the summed chemical equations.

( Reaction 3 )

2 NH₃ + AgCl(s) ⇌ Ag(NH₃)₂¹⁺ + Cl¹⁻

K = K_spK_f = (1.8 × 10⁻¹⁰)(1.7 × 10⁷) = 3.1 × 10⁻³

K = 3.1 × 10⁻³ =

[Ag(NH₃)₂¹⁺][Cl¹⁻]

[NH₃]²

Reaction 1 describes the solubility of AgCl in water, while Reaction 3 describes its solubility in aqueous NH₃. We examine the solubility of AgCl in NH₃ in the following exercise.

8.5-2. AgCl in NH₃ Exercise

Exercise 8.16:

What is the solubility of AgCl in 1.0 M NH₃?

Use x as the solubility of AgCl (x mol/L of AgCl dissolve) to fill in the reaction table. Note that AgCl is a solid, so there are no entries under it. (K = 3.1 × 10^–3 for the reaction below.)

	2 NH₃	+	AgCl(s)	⇌	Ag(NH₃)₂¹⁺	+	Cl^1–
initial	1.0_0_2_ The concentration of ammonia is given in the question.				0_0__ There is none initially.		0_0__ There is none initially.	M
Δ	o_-2x_s Apply stoichiometry and the fact that x mol/L of AgCl dissolve. Don't forget to include the sign.				o_+x_s Apply stoichiometry and the fact that x mol/L of AgCl dissolve. Don't forget to include the sign.		o_+x_s Apply stoichiometry and the fact that x mol/L of AgCl dissolve. Don't forget to include the sign.	M
equilibrium	o_1.0-2x_s Add the initial and Δ lines.				o_x_s Add the initial and Δ lines.		o_x_s Add the initial and Δ lines.	M

Set up the equilibrium constant expression using the equilibrium line entries. Take the square root of both sides and solve for x, the molar solubility.

solubility of AgCl =

0.050_0_2_

K = 3.1e−3 =

[Ag(NH₃)₂¹⁺][Cl¹⁻]

[NH₃]²

x²

(1.0 − 2x)²

Take the square root of both sides to obtain

0.056 =

1.0 − 2x

Multiply both sides by

1.0 − 2x

to remove the denominator to get

0.056(1.0 − 2x) = x.

Gather terms:

0.056 = 1.11x,

solve for x.

x =

0.056

1.11

= 0.050 M

8.5-3. Acids and Bases Dissolve One Another

The solubility of AgCl is 4 × 10³ times greater in 1 M ammonia than in water. In fact, it is a general principle that an insoluble salt can be dissolved by placing it into a solution of a Lewis base (OH^1–, CN^1–, or NH₃) with which the metal forms a complex ion. However, the metal goes into solution predominantly as the complex ion, not as the free metal ion. Dissolving an insoluble salt by forming a complex ion is a Lewis acid-base reaction. Ag¹⁺ is a Lewis acid and Cl^1– and NH₃ are bases that can compete for the Lewis acid. In cases where the anion is a weak base, the insoluble salt can be dissolved by placing it in strong acid. For example, CN^1– is a base and Ag¹⁺ and H₃O¹⁺ are acids that can compete for the base. An example of this type is considered in the following exercise.

8.5-4. Determining K Exercise

Exercise 8.17:

F^1– ion is a weak base that can react with acids. In this exercise, we use the solubility of CaF₂ in a strong acid to examine the competition between H₃O¹⁺ and Ca²⁺ for the F^1– ion.

What is the equilibrium constant for the dissociation of CaF₂ in strong acid?

CaF₂(s) + 2 H₃O¹⁺ ⇌ Ca²⁺ + 2 HF + 2 H₂O

•

K_sp for CaF₂ = 3.9 × 10⁻¹¹
•

K_a for HF = 7.2 × 10⁻⁴

1. The chemical equation for the K_sp of CaF₂ is the following. (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a caret (^). For example, NH_4^1+ for NH₄¹⁺. Include any coefficients other than 1. Omit any spaces.)

o_CaF_2_s CaF₂ ⇌ Ca²⁺ + 2F^1–

⇌

o_Ca^2+_s CaF₂ ⇌ Ca²⁺ + 2F^1–

o_2F^1-_s CaF₂ ⇌ Ca²⁺ + 2F^1–

2. By what number should the above be multiplied? Use a negative sign to indicate that the direction of the reaction must be reversed from the defined direction.
multiply CaF₂ dissociation by

1_0__ One mole CaF₂ appears as a reactant in both the dissociation reaction and the above reaction, so the reaction does not need to be changed.

3. The equilibrium constant for the reaction produced in Step 2:

K = 3.9e-11_0__ The reaction is the same as the Ksp reaction, so

K = K_sp.

4. The chemical equation for the K_a of HF is the following. (Indicate any subscripted characters with an underscore (_) and any superscripted characters with a caret (^). For example, NH_4^1+ for NH₄¹⁺. Include any coefficients other than 1. Omit any spaces.)

o_HF_s HF + H₂O ⇌ H₃O¹⁺ + F^1–

o_H_2O_s HF + H₂O ⇌ H₃O¹⁺ + F^1–

⇌

o_H_3O^1+_s HF + H₂O ⇌ H₃O¹⁺ + F^1–

o_F^1-_s HF + H₂O ⇌ H₃O¹⁺ + F^1–

5. By what number should the above be multiplied? Use a negative sign to indicate that the direction of the reaction must be reversed from the defined direction.
multiply HF dissociation by

-2_0__ One mole HF₂ is a reactant in the acid dissociation reaction, but two moles of HF are produced in the above reaction. Thus, the K_a reaction must be reversed and multiplied by 2.

6. The equilibrium constant for the reaction produced in Step 5:

K = 1.9e6_0__ Reversing a reaction requires taking the reciprocal of K, and multiplying a reaction by 2 requires squaring K. Thus,

K = (1/K_a)².

7. The equilibrium constant for dissolving CaF₂ in acid:

K = 7.5e-5_0__ The equilibrium constant is the product of the two equilibrium constants for the reactions that summed to the desired reaction.

K = (3.9e−11)(1.9e6) = 7.5e−05

8.5-5. Solubility of Ag₃PO₄

Exercise 8.18:

In Section 8.2-5., we saw that the solubility of Ag₃PO₄ in water was over eight times greater than that determined with K_sp due to a competition between Ag¹⁺ and H₂O for PO₄^3–. We now revisit that solubility as a competing equilibria problem. We assume that the equilibrium can be determined with the following:

Ag₃PO₄(s) ⇌ 3 Ag¹⁺ + PO₄^3– K_sp = 2.6 × 10^–18

PO₄^3– + H₂O ⇌ HPO₄^2– + OH^1– K_b = 0.021

Assume that the reaction is Ag₃PO₄(s) + H₂O ⇌ 3 Ag¹⁺ + HPO₄^2– + OH^1– and determine the equilibrium constant for the solubility:

K =

5.5e-20_0__ Adding the two chemical equations produces the desired equation, so K = K_spK_b.

If the pH of a saturated solution is 9.00, what is the solubility of Ag₃PO₄? As shown in Figure 7.3, all phosphate is in the form of HPO₄^2– at pH = 9.00.

solubility =

1.2e-4_0__ K = [Ag¹⁺]³[HPO₄^2–][OH^1–]; [Ag¹⁺] = 3x; [HPO₄^2–] = x; [OH^1–] = 10^–pOH = 10^–5.00

The observed solubility is 1.5 × 10^–4 M, but that determined with K_sp alone is 1.8 × 10^–5 M. Thus, it is competing equilibria like this that lead to such poor agreement between predicted and experimental solubilities for salts of relatively strong bases when only K_sp is used in the calculations.

8.6 Exercises and Solutions

Select the links to view either the end-of-chapter exercises or the solutions to the odd exercises.

•
End-of-Chapter Exercises
•
Solutions to Odd Exercises

AgCl: x	=	(1.2e−10)^1/2
	~	1e−5 M

AgCl: x	=	(1.2e−10)^1/2
	~	1e−5 M

TlCl: x	=	(1.9e−4)^1/2
	=	0.014 M

TlCl: x	=	(1.9e−4)^1/2
	=	0.014 M

Chapter 8 – Equilibria Containing Metal Ions

Introduction

8.1 Acid-Base Equilibria

Introduction

Objectives

8.1-1. Metal Ions as Acids

8.2 Dissolution and the Solubility Product Constant

Introduction

Objectives

8.2-1. The Solubility Product

8.2-2. Ksp from Solubility Exercise

8.2-3. Ksp from pH Exercise

8.2-4. Solubility from Ksp Exercise

8.2-5. Ksp and Strong Bases

8.2-6. Cation:Anion Ratios in Ksp

8.2-7. Determining Relative Solubilities Exercise

8.2-8. Predicting the More Soluble Salt Exercise

8.2-9. Common-Ion Effect

8.2-10. Common-Ion Solubility from pH Exercise

8.2-11. Solubility of AgCl Exercise

8.3 Precipitation and Separation of Ions

Introduction

Objectives

8.3-1. The Ion Product

8.3-2. Identifying Precipitating Hydroxides Exercise

8.3-3. Identifying Precipitating Chlorides Exercise

8.3-4. Determining a Required Concentration

8.3-5. Determining pH at which Precipitate Forms Exercise

8.3-6. Separations

8.3-7. Optimum Separation Exercise

8.3-8. Reaction Table Exercise

8.3-9. Reaction Table Exercise

8.4 Complex Ions

Introduction

Objectives

8.4-1. The Formation and Dissociation Constants

8.4-2. Exercise

8.4-3. Separations with Sulfide Ion

8.4-4. Sulfide Separation Exercise

8.5 Competing or Simultaneous Equilibria

Introduction

Objectives

8.5-1. Silver Chloride Dissolves in Ammonia

8.5-2. AgCl in NH3 Exercise

8.5-3. Acids and Bases Dissolve One Another

8.5-4. Determining K Exercise

8.5-5. Solubility of Ag3PO4

8.6 Exercises and Solutions

8.2-2. K_sp from Solubility Exercise

8.2-3. K_sp from pH Exercise

8.2-4. Solubility from K_sp Exercise

8.2-5. K_sp and Strong Bases

8.2-6. Cation:Anion Ratios in K_sp

8.5-2. AgCl in NH₃ Exercise

8.5-5. Solubility of Ag₃PO₄