Chapter 5 – Chemical Equilibrium
Introduction
The equilibrium constant was defined in Chapter 4, and calculations were done to establish the relationship between it and the standard free energy change of the reaction. However, the equilibrium constant is most valuable because it lets us predict the composition of an equilibrium mixture or to adjust the reactant concentrations so as to obtain an equilibrium mixture with the desired composition. These calculations are so important that they form the basis of this chapter and much of Chapters 6, 7, and 8, where the principles established in this chapter are applied to proton transfer, solubility, and electron transfer processes, respectively.5.1 The Equilibrium Constant
Introduction
The thermodynamic equilibrium constant discussed in Chapter 4 is unitless because it is defined in terms of unitless activities. However, equilibrium constants can be defined in terms of partial pressures or molar concentrations. These equilibrium constants typically, but not always, have units. In this section, we introduce both types of equilibrium constants, show how to convert from one to the other, and demonstrate some of their properties.Objectives
-
•Determine the value of K for a reaction given the value of K for a related reaction that differs only by a multiple or in direction.
-
•Determine the equilibrium constant of a reaction that is the sum of several other reactions.
-
•Convert between Kp and Kc.
Kp Versus Kc
5.1-1. Kp and Kc Defined
An equilibrium constant in which partial pressures are used for activities is called Kp, while one in which molar concentrations are used for activites is called Kc. For a reaction that involves only gases, Kp equals K (the thermodynamic equilibrium constant that has no units) if the partial pressures are in atmospheres because the activity of a gas is numerically equal to its partial pressure in atmospheres. For a reaction that involves only solutes in a liquid solution, Kc equals K because the activity of a solute is numerically equal to its molar concentration. Consider the following equilibrium:N2 + 3 H2 ⇌ 2 NH3
Kp =
| (PNH3)2 atm2 |
| (PN2) atm · (PH2)3 atm3 |
-
•the units of Kp are atmΔng
-
•the units of Kc are MΔng
5.1-2. Converting Between Kp and Kc
Since the thermodynamic K equals Kp for gas phase equilibria, Kp values are a common way to discuss their equilibria. However, there are times when it is more convenient to consider gas phase equilibria in terms of molar concentrations; i.e., in terms of Kc. In such cases, the Kp would have to be converted into a Kc. The conversion involves converting the partial pressures of the gases into molar concentrations, which is done with the ideal gas law. We first express the partial pressure of gas A in terms of its pressure as follows: where PA is the partial pressure of A, nA is the number of moles of gas A. nA/V is the number of moles of A per liter of gas, which is [A], the molar concentration of A. Substitution of nA/V = [A] into the above equation yields Equation 5.1, which relates the concentration of a gas to its partial pressure. Substitution of [A]RT for PA into a Kp expression converts the expression from one of pressures to one of concentrations; i.e., it converts the Kp into a Kc. Equation 5.2 summarizes the relationship.5.1-3. Converting with the Factor Label Method
If remembering which sign of Δng to use is a problem, then Kp ⇌ Kc conversions can be done as factor label conversions in which units of (atmΔng) are converted into units of (MΔng) using RT as the conversion factor. R, which is the ideal gas law constant, equals 0.08206 L·atm·K–1·mol–1. However, it can be made more useful for converting between atm and M by recognizing that L·mol–1 = M–1, so the units of R can be expressed as atm·K–1·M–1, so-
•RT has units of atm·M–1 = atm/M.
5.1-4. Thermodynamics and K Exercise
Exercise 5.1:
What are K, Kp, and Kc for the following at 298 K if ΔG° = –31.0 kJ?
When writing units, indicate superscripts with a carat. For example, atm^3 = atm3. Enter none if there are no units.
N2(g) + 3 H2(g) ⇌ 2 NH3(g)
Δng =
-2_0__
2 mol produced – 4 mol react

| Value | Units | |||||||
|---|---|---|---|---|---|---|---|---|
| K |
2.7e5_0__
Use the equation
K = exp
K = exp(12.5) = 2.7e5
|
o_none_ins
The thermodynamic K has no units.
|
||||||
| Kp |
2.7e5_0__
Kp = K for a gas-phase reaction
|
o_atm^-2_s
The units of Kp are atmΔng, so units are atm–2.
|
||||||
| Kc |
1.6e8_0__
|
o_M^-2_s
The units of Kc are MΔng, so units are M–2.
|
5.1-5. Exercise
Exercise 5.2:
Convert the given Kp to Kc at 298 K.
| Reaction | Kp | |
|---|---|---|
| (a) | H2O(l) ⇌ H2O(g) | 0.031 atm |
| (b) | H2(g)+ I2(g) ⇌ 2 HI(g) | 622 |
| (c) | N2(g)+ 3 H2(g) ⇌ 2 NH3(g) | 6.1e5 atm–2 |
RT =
24.5_0__
RT = (0.0821)(298) = 24.5 atm/M
atm·M–1

| Δng | Kc | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (a) |
1_0__
There is one mole of produced gas but no reacting gas.
mol
|
1.3e-3_0__
|
||||||||
| (b) |
0_0__
There are two moles of produced gas and two moles of reacting gas.
mol
|
622_0__
Δng = 0, so Kc = Kp
|
||||||||
| (c) |
-2_0__
There are four moles of reacting gas but only two moles of produced gas.
mol
|
3.7e8_0__
|
Properties of the Equilibrium Constant
5.1-6. Properties
We will use the following two aqueous equilibria for our discussions of the properties of the equilibrium constant:( Equilibrium 1 )
A(aq) ⇌ B(aq) K1 =
= 5
| [B] |
| [A] |
( Equilibrium 2 )
B(aq) ⇌ C(aq) K2 =
= 0.3
| [C] |
| [B] |
-
•If the coefficients of a chemical equation are all multiplied by some number n, then the equilibrium constant of the resulting chemical equation equals the original equilibrium constant raised to the nth power: K' = K n. For example, multiplying Equilibrium 1 by 3, we obtain
3 A(aq) ⇌ 3 B(aq) K = K13 =
= 53 = 125
| [B]3 |
| [A]3 |
-
•If the direction of the equation is reversed, then the equilibrium constant of the resulting equation is the reciprocal of the original equilibrium constant:K' = 1/K.For example, reversing Equilibrium 1, we obtain
B(aq) ⇌ A(aq) K = K1–1 =
= 5−1 = 0.2
| [A] |
| [B] |
-
•If two chemical equations are added, then the equilibrium constant of the resulting equation is the product of the two original equilibrium constants. For example, adding Equilibria 1 and 2, we obtain A(aq) ⇌ C(aq), and the equilibrium constant is then determined as follows:
A(aq) ⇌ C(aq) K = K1K2 =
×
=
= (5)(0.3) = 1.5
| [B] |
| [A] |
| [C] |
| [B] |
| [C] |
| [A] |
5.1-7. Exercise
Exercise 5.3:
Given the following equilibrium constants,
| Reaction | K | |
|---|---|---|
| 1 | HF(aq) + H2O(l) ⇌ F1–(aq) + H3O1+(aq) | 7.2e–4 |
| 2 | HNO2(aq) + H2O(l) ⇌ NO21–(aq) + H3O1+(aq) | 4.0e–4 |
Determine the value of the equilibrium constants of the following.
| Reaction | K |
|---|---|
| F1–(aq) + H3O1+(aq) ⇌ HF(aq) + H2O(l) |
1.4e3_0__
This reaction is the reverse of Equation 1, so K = (7.2e–04)–1.
|
| F1–(aq) + HNO2(aq) ⇌ HF(aq) + NO21–(aq) |
0.56_0__
This reaction is the sum of Equation 2 and the reverse of Equation 1, so K = (4.0e–04)(7.2e–04)–1.
|
5.1-8. Exercise
Exercise 5.4:

Given the following equilibrium constants,
-
1HF(aq) + H2O(l) ⇌ F1−(aq) + H3O1+(aq) K1 = 7.2e−4
-
2CaF2(s) ⇌ Ca2+(aq) + 2 F1−(aq) K2 = 3.9e−11
Determine the equilibrium constant for the following reaction.
CaF2(s) + 2 H3O1+(aq) ⇌ Ca2+(aq) + 2 HF(aq) + 2 H2O(l)
First determine how to sum Equations 1 and 2 to obtain the desired equation.
Which chemical equation must be reversed?
-
Equation 1
-
Equation 2 CaF2 is a reactant in Equation 2 and the requested equation, so Equation 2 does not need to be reversed. HF is a reactant in Equation 1 and a product in the desired equation.

Equation 1 must be multiplied by what integer?
2_0__
The coefficient of HF in Equation 1 is 1, but it is 2 in the desired equation.

Equation 2 must be multiplied by what integer?
1_0__
The coefficient of CaF2 is 1 in both Equation 2 and the desired equation.

K =
7.5e-5_0__

K = K1−2K2 = K2/K12
5.2 Le Châtelier's Principle
Introduction
In Chapter 4, the spontaneous direction of a reaction was predicted from known concentrations by using the fact that a reaction proceeds from left to right whenQ < K
and from right to left when Q > K.
We also saw that a temperature rise causes the equilibrium constants of endothermic reactions to increase and the equilbirium constants of exothermic reactions to decrease. However, the same conclusions can be drawn without calculation by applying Le Châtelier's Principle. In this section, we apply this important principle to three types of disturbances:
-
•changing an amount of a reactant or product
-
•changing the volume
-
•changing the temperature
Objectives
-
•Explain how Le Châtelier's Principle is a summary of the relationship between Q and K of the reaction.
-
•Use Le Châtelier's Principle and considerations of the reaction quotient and the equilibrium constant to predict the direction of the shift in equilibrium caused by stress placed on the equilibrium.
5.2-1. Statement of Le Châtelier's Principle
Le Châtelier's Principle-
•If a system at equilibrium is disturbed, then the system reacts so as to counteract the disturbance.
5.2-2. Changing the Amount of a Substance
Consider Figures 5.1a–c, which show the effect of changing one concentration in an equilibrium mixture ofA + B ⇌ C + D.
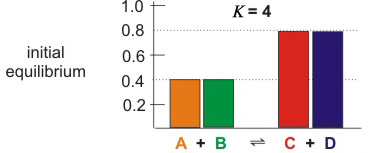
Figure 5.1a: Effect of Adding and Removing Substances from an Equilibrium Mixture
The colored rectangles represent the concentrations of each of the substances.
K =
=
= 4.0
| [C][D] |
| [A][B] |
| (0.80)(0.80) |
| (0.40)(0.40) |
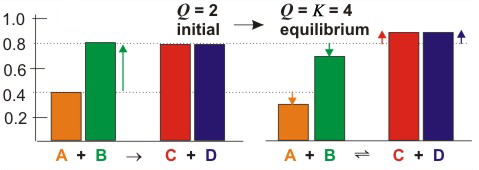
Figure 5.1b: Effect of Adding and Removing Substances from an Equilibrium Mixture
The colored rectangles represent the concentrations of each of the substances. Figures on the left correspond to the concentrations immediately after the change occurs, while those on the right represent the resulting equilibrium concentrations.
Q < K,
and the reaction proceeds to the right, which has the effect of reducing [B]
as predicted by Le Châtelier's Principle. Thus, B reacts with A to produce C and D. The changes in concentration resulting from the reaction cause Q to increase, which it does until it equals K and equlibrium is re-established. We use the symbol Δ for the changes in concentration; i.e., [A] and [B] each decrease by Δ, while [C] and [D] each increase by Δ. The magnitude of Δ is given by the arrows on the right side of the figure. We will show how to determine the value of Δ in the following section, but now we simply state that a Δ = 0.105 M
is required to restore equilibrium, so the new concentrations would be the following:
-
•[A] = 0.400 – Δ = 0.40 – 0.105 = 0.295 M
-
•[B] = 0.800 – Δ = 0.80 – 0.105 = 0.695 M
-
•[C] = [D] = 0.800 + Δ = 0.80 + 0.105 = 0.905 M
Q =
= 4.0 = K
| (0.905)2 |
| (0.295)(0.695) |
Q = K
at these concentrations, so the system is back to equilibrium.

Figure 5.1c: Effect of Adding and Removing Substances from an Equilibrium Mixture
The colored rectangles represent the concentrations of each of the substances. Figures on the left correspond to the concentrations immediately after the change occurs, while those on the right represent the resulting equilibrium concentrations.
Q = (0.20)(0.80)/(0.40)2 = 1.0.
Q < K,
so again the reaction proceeds to the right and Q increases again until Q = K
and equilibrium is re-established. Again the extent of reaction, Δ, is represented by the arrows on the right side of the figure. In this case, Δ = 0.125 M,
which produces the following concentrations:
-
•[A] = [B] = 0.400 – Δ = 0.400 – 0.125 = 0.275 M
-
•[C] = 0.200 + Δ = 0.200 + 0.125 = 0.325 M
-
•[D] = 0.800 + Δ = 0.800 + 0.125 = 0.925 M
Q =
= 4.0 = K
| (0.325)(0.925) |
| (0.275)2 |
Q = K,
so the new concentrations are indeed equilibrium concentrations.
5.2-3. Changing the Volume
Changing the volume changes the pressures of the gases, and Le Châtelier's Principle states that an equilibrium mixture reacts to counteract the change. At constant temperature, the only way to change the pressure is to change the number of moles of gas. Consequently, equilibrium mixtures react so as to increase the number of moles of gas when the volume of the mixture is increased or decrease the number of moles of gas when the volume is decreased. Changing the volume changes both the pressures and the concentrations of the gases, which changes Q. The change in Q depends upon Δng in such a way that the same conclusions are drawn from Q and K considerations as with Le Châtelier's Principle.5.2-4. Changing the Temperature
Changing the temperature at constant pressure changes K not Q, and Le Châtelier's Principle summarizes the effect that temperature has on the equilibrium constant. Heat can be viewed as a product of an exothermic reaction and as a reactant in an endothermic reaction. Heating an exothermic reaction is the same as adding a product, which shifts the reaction toward the reactant side (←). The shift increases the equilibrium concentrations of the reactants and decreases the equilibrium concentrations of the products. The result is that the value of K is decreased in agreement with the conclusion reached using the equationln(K2) = ln(K1) +
−
.
| ΔH° |
| R |
 |
| 1 |
| T1 |
| 1 |
| T2 |
 |
5.2-5. Exercises
Exercise 5.5:




Apply Le Châtelier's Principle to determine the effect on the equilibrium pressure of N2.
-
Adding H2:
-
increase Some nitrogen must react with some of the added hydrogen.
-
decrease
-
no change Some nitrogen must react with some of the added hydrogen.

-
Removing NH3:
-
increase Some nitrogen must react with hydrogen to replace the ammonia.
-
decrease
-
no change Some nitrogen must react with hydrogen to replace the ammonia.

-
Increasing the volume:
-
increase
-
decrease There are four moles of reacting gas and only 2 moles of produced gas.
-
no change There are four moles of reacting gas and only 2 moles of produced gas.

-
Increasing the temperature:
-
increase
-
decrease Heat is a product of the reaction (exothermic), so increasing the temperature would shift the reaction back toward the reactant side.
-
no change Heat is a product of the reaction (exothermic), so increasing the temperature would shift the reaction back toward the reactant side.

Exercise 5.6:




Indicate the effect on the equilibrium concentration of Ag1+ caused by the following.
-
Dissolving solid AgNO3 in the solution:
-
increase
-
decrease Dissolving silver nitrate increases the silver ion concentration.
-
no change Dissolving silver nitrate increases the silver ion concentration.

-
Adding solid AgCl to the solution:
-
increase AgCl appears as a solid in the chemical equation, so it does not appear in the expression for Q. Consequently, adding the solid has no effect.
-
decrease AgCl appears as a solid in the chemical equation, so it does not appear in the expression for Q. Consequently, adding the solid has no effect.
-
no change

-
Increasing the temperature:
-
increase
-
decrease Heat is a reactant (endothermic reaction), so increasing the temperature drives the reaction toward the product side.
-
no change Heat is a reactant (endothermic reaction), so increasing the temperature drives the reaction toward the product side.

-
Adding water:
-
increase Q = [Ag1+][Cl1–]. Adding water decreases the concentrations, soQ < Kand the reaction shifts toward the right to produce chloride ion. However, the volume increases as well so as to maintain a constant concentration of chloride ion. The concentration is called the solubility of AgCl.
-
decrease Q = [Ag1+][Cl1–]. Adding water decreases the concentrations, soQ < Kand the reaction shifts toward the right to produce chloride ion. However, the volume increases as well so as to maintain a constant concentration of chloride ion. The concentration is called the solubility of AgCl.
-
no change

Exercise 5.7:



Indicate the effect on the hydrogen sulfate ion concentration of the following.
-
Adding Pb(NO3)2(aq), which precipitates PbSO4 from the solution:
-
increase Precipitating PbSO4 reduces the SO42– ion concentration, so some HSO41– reacts to replace some of the lost SO42– ion.
-
decrease
-
no change Precipitating PbSO4 reduces the SO42– ion concentration, so some HSO41– reacts to replace some of the lost SO42– ion.

-
Adding hydrochloric acid to increase [H3O1+]:
-
increase
-
decrease SO42– ion would react with the additional H3O1+ to produce HSO41–.
-
no change SO42– ion would react with the additional H3O1+ to produce HSO41–.

-
Warming the solution:
-
increase
-
decrease The reaction is exothermic, so heat is a product. Warming the solution would cause reaction away from the heat, which would produce some HSO41–. The increase in HSO41– and decrease in H3O1+ and SO42– results because the equilibrium constant is decreased.
-
no change The reaction is exothermic, so heat is a product. Warming the solution would cause reaction away from the heat, which would produce some HSO41–. The increase in HSO41– and decrease in H3O1+ and SO42– results because the equilibrium constant is decreased.

5.3 Using the Equilibrium Constant
Introduction
The stoichiometry problems of Chapter 1 all assumed that the limiting reactant disappeared completely during reaction. However, this assumes that the equilibrium constant is very large. In this section, we address problems in which the equilibrium constant is not very large, so the limiting reactant does not disappear completely. We will again use a reaction table as introduced in Chapter 1. The reaction table consists of three lines: the initial, change, and final. In equilibrium problems, the unknown can lie on any one of these lines or it can require filling in the table to determine the value of the equilibrium constant. In this section we show how to solve equilibrium problems.Objectives
-
•Calculate the concentrations of one substance in an equilibrium mixture from the other concentrations and the equilibrium constant.
-
•Determine the equilibrium constant for a reaction given the initial amounts and one equilibrium amount.
-
•Determine the equilibrium composition from the initial composition and the equilibrium constant.
-
•Calculate the amount of one reactant required to react with a given amount of another reactant to produce a given amount of product.
-
•Determine the extent of the change caused by the addition of known amounts of reactants or products to an equilibrium mixture, given K and the initial equilibrium concentrations.
-
•Calculate the amount of one substance that would have to be added to an equilibrium to change the concentration of another substance in the equilibrium by a given amount.
Solving for One Concentration when K and the Other Concentrations are Known
5.3-1. Determining an Unknown Concentration
We begin with the easiest of equilibrium problems: determining an unknown concentration when all other concentrations and the equilibrium constant are known. Solving this type of problem involves setting up the equilibrium constant expression, solving it for the unknown, and substituting the known values into the resulting expression. The next two exercises demonstrate the process.5.3-2. Exercise
Exercise 5.8:
What is the acetate ion concentration in a solution in which [CH3COOH] = 0.10 M and [H3O1+] = 1.0e–5 M? Recall that Ka is the equilibrium constant for the reaction of an acid with water and is referred to as the acid dissociation constant.
CH3COOH(aq) + H2O(l) ⇌ CH3COO1−(aq) + H3O1+(aq) Ka = 1.8e−5
[CH3COO1–] =
0.18_0__

[CH3COO1−] =
=
M
| Ka[CH3COOH] |
| [H3O1+] |
| (1.8e−5)(0.10) |
| 1.0e−5 |
5.3-3. Exercise
Exercise 5.9:
What is the maximum calcium ion concentration that can exist in equilibrium with [H3O1+] =
0.10 M and
[HF] = 0.20 M?
CaF2(s) + 2 H3O1+(aq) ⇌ Ca2+(aq) + 2 HF(aq) + 2 H2O(l) K = 7.5e−5
[Ca2+] =
1.9e-5_0__
CaF2 and H2O are pure substances 
(a = 1),
so [Ca2+] =
=
| K[H3O1+]2 |
| [HF]2 |
| (7.5e−5)(0.10)2 |
| (0.20)2 |
Using Reaction Tables in Equilibrium Problems
5.3-4. Filling in the Reaction Table
The amount of a substance present in an equilibrium mixture is determined from the concentrations of all reactants and products, not just a single limiting reactant, and the reaction table is again the best way to track the changes. However, the label of the last line is changed from "final" to "eq" to emphasize that equilibrium is established. The Δ line represents the amount of each substance that must form or react in order to change from initial to equilibrium concentrations. When making entries into it, remember the following:-
•It is the only line to which stoichiometry applies. If one entry on the Δ line is known, then all other entries can be determined by stoichiometry.
-
•If the initial system must shift to the right (→,Q < K),the concentrations of everything on the right (product) side of the reaction must increase (Δ > 0), while all concentrations on the left side must decrease (Δ < 0).
-
•If the shift is to the left (←,Q > K),the concentrations of everything on the left side must increase(Δ > 0),while the concentrations of everything on the right side must decrease (Δ < 0).
5.3-5. Types of Equilibrium Problems
We will be doing equilibrium problems in most of the remaining chapters as we examine acid-base, solubility, and redox equilibria. However, there are only three different kinds of equilibrium problems:-
1Determine K from the equilibrium concentrations. If K is the unknown, then the reaction table can contain no unknowns.
-
2Determine the equilibrium concentrations from K and a set of initial concentrations. The unknown is in the Δ line and therefore also in the equilibrium line. We will use x as our unknown identifier.
-
3Determine the amount of substance that must be added (removed) to (from) a known amount of another reactant to produce a desired equilibrium concentration. The unknown is in the initial line.
Determining K
5.3-6. Method
In order to determine K, you must be given sufficient information to determine the equilibrium concentrations. This information can be given directly, but many times only the initial concentrations and the final concentration of just one of the substances are given. Setting up a reaction table is the easiest way to establish the other concentrations. In these cases, use the following method:1
Enter the given concentrations into the reaction table.
2
Determine the entry on the Δ line of the substance whose final concentration is given by
subtracting the initial concentration from the equilibrium concentration: Δ = eq – initial.
3
Determine the other entries on the Δ line by applying stoichiometry to the entry determined in
Step 2.
4
Determine the other equilibrium concentrations by adding the initial and
Δ lines.
5
Use the equilibrium concentrations determined in Step 4 to determine
K.
5.3-7. Kc for a Gas Phase Reaction
Exercise 5.10:
At some temperature, 6.0 moles of hydrogen and 4.0 moles of nitrogen are added to a 10.0 L flask and allowed to react. At equilibrium, there is 1.0 mole of hydrogen remaining. What is the value of Kc for the following reaction at this temperature? Fill in the reaction table in molar concentrations, then determine K.
Include the signs in the Δ line, even when positive.
| WaTeX parsing error. | + |
3 H2(g)
|
⇌ |
2 NH3(g)
|
||
|---|---|---|---|---|---|---|
| initial |
.40_0_2_
The initial molar concentration is determined by dividing the initial number of moles by the volume of the flask.
|
0.60_0_2_
The initial molar concentration is determined by dividing the initial number of moles by the volume of the flask.
|
0_0__
There is no ammonia initially.
|
M | ||
| Δ |
-0.17_0__
The stoichiometry of the reaction indicates that the amount of N2 that reacts is 1/3 of the amount of H2 that reacts. N2 disappears, so the change is negative.
|
-0.50_0_2_
The flask was 0.60 M in H2 initially but only
0.10 M at equilibrium. The difference is the amount that reacts. H2 disappears, so the change is negative.
|
o_+0.33_s
The stoichiometry of the reaction indicates that the amount of NH3 that forms is 2/3 of the amount of H2 that reacts. NH3 forms, so the change is positive.
|
M | ||
| eq |
0.23_0__
The equilibrium concentration is simply the sum of the initial and Δ lines.
|
0.10_0_2_
The equilibrium number of moles of H2 is given, but it must be converted into a molar concentration.
|
0.33_0__
The equilibrium concentration is simply the sum of the initial and Δ lines.
|
M |
Kc =
4.7e2_0__

K =
=
= 4.7e2
M–2
| [NH3]2 |
| [N2][H2]3 |
| (0.33)2 |
| (0.23)(0.10)3 |
5.3-8. Aqueous Reaction
Exercise 5.11:
10. mmol of NH4Cl and 15 mmol of KCN are dissolved in enough water to make 200. mL of
solution. What is the value of the equilibrium constant of the following reaction if [NH41+] = 0.018 M at equilibrium? Fill in the reaction table and then use the equilibrium values to determine K. The entries in the Δ line must include the sign.
| NH41+(aq) | + |
CN1−(aq)
|
⇌ |
NH3(aq)
|
+ |
HCN(aq)
|
||
|---|---|---|---|---|---|---|---|---|
| initial |
0.050_0_2_
Divide the given number of millimoles by the total volume in milliliters.
|
0.075_0_2_
Divide the given number of millimoles by the total volume in milliliters.
|
0_0__
There is none initially.
|
0_0__
There is none initially.
|
M | |||
| Δ |
-0.032_0__
The initial and final concentrations are 0.050 M and 0.018 M, respectively. The difference is the change.
|
-0.032_0__
The reaction stoichiometry is 1:1:1:1, so the magnitude of the change is the same as from NH41+. The CN1– reacts, so the sign is negative.
|
o_+0.032_s
The reaction stoichiometry is 1:1:1:1, so the magnitude of the change is the same as from NH41+. The NH3 is formed, so the sign is positive.
|
o_+0.032_s
The reaction stoichiometry is 1:1:1:1, so the magnitude of the change is the same as from NH41+. The HCN is formed, so the sign is positive.
|
M | |||
| eq |
0.018_0__
This equilibrium concentration is given.
|
0.043_0__
The equilibrium concentration is the sum of the initial and Δ lines.
|
0.032_0__
The equilibrium concentration is the sum of the initial and Δ lines.
|
0.032_0__
The equilibrium concentration is the sum of the initial and Δ lines.
|
M |
K =
1.3_0__

K =
=
| [NH3][HCN] |
| [NH41+][CN1−] |
| (0.032)(0.032) |
| (0.018)(0.043) |
Determining Equilibrium Amounts
5.3-9. Method
If you are asked for an equilibrium concentration or pressure, you must be given the value of K and the initial conditions. The unknown (x) is in the reaction table. To find equilibrium concentrations or pressures given the equilibrium constant and the initial concentrations, use the following method.1
Put the initial quantities in the reaction table.
2
If both reactants and products are present, calculate Q and determine the direction in which the reaction is proceeding by comparing Q and K. This will help you decide upon the signs to use with the entries on the Δ line.
3
Use x's to complete the Δ line. To simplify stoichiometry considerations, the coefficient of x in each entry should be the same as the coefficient in the balanced equation for that substance. Be sure to include the proper sign.
4
Add the initial and final lines to get the equilibrium line.
5
Substitute the equilibrium line entries into the equilibrium constant expression and solve for x.
6
Use the value of x determined in Step 5 and the expressions for the equilibrium concentrations to determine the equilibrium concentrations or pressures.
5.3-10. Hints to Simplify the Problems
Equilibrium problems involving gas phase reactions in which Δng = 0 can be done in moles rather than molarities because the volumes cancel.
Δng = 0 can be done in moles rather than molarities. However, if Δng is not zero, you must convert to molarities in order to use a Kc.
Taking the square root of both sides of the equilibrium expression will
often simplify the algebra.
5.3-11. Equilibrium Moles
Exercise 5.12:
0.80 mol N2 and 0.80 mol O2 are mixed and allowed to
react in a 10 L vessel at 2500 °C. How many moles
of nitric oxide would be present when the equilibrium is established? Use x as the unknown identifier.
Hint: You are given moles and are asked for moles, and Δng = 0, so the problem can be done in moles with the given equilibrium constant.
|
N2
|
+ |
O2
|
⇌ |
2 NO
|
K = 2.1e–3 | |
|---|---|---|---|---|---|---|
| initial |
0.80_0_2_
Use the given number of moles.
|
0.80_0_2_
Use the given number of moles.
|
0_0__
There is no NO initially.
|
mol | ||
| Δ |
o_-x_s
The amount that reacts is unknown. The reaction will proceed to form NO, so N2 disappears and its coefficient is 1. This entry should be
−x.
|
o_-x_s
The amount that reacts is unknown. The reaction will proceed to form NO, so O2 disappears and its coefficient is 1. This entry should be
−x.
|
o_+2x_s
The amount that forms is unknown. The reaction will proceed to form NO, and its coefficient is 2, so this entry should be
+2x.
|
mol | ||
| eq |
o_0.80-x_s
Sum the initial and Δ lines to get
0.80−x.
|
o_0.80-x_s
Sum the initial and Δ lines to get
0.80−x.
|
o_2x_s
Sum the initial and Δ lines to get
2x.
|
mol |
The equilibrium constant expression is a perfect square, so take the square
root of both sides and solve for x.
x =
0.018_0__
Take the square root of both sides to simplify.
Multiply both sides by
mol

2.1e−3 =
=
| (2x)2 |
| (0.80 − x)(0.80 − x) |
| (2x)2 |
| (0.80 − x)2 |
Take the square root of both sides to simplify.
4.6e−2 =
| (2x) |
| (0.80 − x) |
Multiply both sides by
(0.80 − x)
to remove the denominator, rearrange to get x on one side, and solve for x.| (4.6e−2)(0.80 − x) | = | 2x → | ||
| 3.7e−2 − (4.6e−2)x | = | 2x → | ||
| 3.7e−2 | = | 2.046x | ||
x =
| = | 0.018 |
moles of NO =
0.036_0__
mol NO = 2x
mol

5.3-12. Determining Equilibrium Pressures
Exercise 5.13:


What are the equilibrium pressures in a mixture if the initial pressures of CO and H2O are each 0.200 atm?
|
CO(g)
|
+ |
H2O(g)
|
⇌ |
CO2(g)
|
+ |
H2(g)
|
K = 10.0
|
|
|---|---|---|---|---|---|---|---|---|
| initial |
0.200_0_3_
The initial pressure is 0.200 atm.
|
0.200_0_3_
The initial pressure is 0.200 atm.
|
0_0__
The initial pressure is 0.
|
0_0__
The initial pressure is 0.
|
atm | |||
| Δ |
o_-x_s
CO disappears and its coefficient is one, so the entry is
−x.
|
o_-x_s
H2O disappears and its coefficient is one, so the entry is
−x.
|
o_+x_s
CO2 forms and its coefficient is one, so the entry is
+x.
|
o_+x_s
H2 forms and its coefficient is one, so the entry is
+x.
|
atm | |||
| eq |
o_0.200-x_s
Sum the initial and final lines to obtain
0.200−x.
|
o_0.200-x_ins
Sum the initial and final lines to obtain
0.200−x.
|
o_x_ins
Sum the initial and final lines to obtain x.
|
o_x_ins
Sum the initial and final lines to obtain x.
|
atm |
The equilibrium constant expression is a perfect square, so take the square
root of both sides and solve for x.
x =
0.152_0__
Take the square root of both sides to simplify.
Multiply both sides by
atm

10.0 =
=
| (x)(x) |
| (0.200 − x)(0.200 − x) |
| (x)2 |
| (0.200 − x)2 |
Take the square root of both sides to simplify.
3.16 =
| x |
| 0.200 − x |
Multiply both sides by
(0.200 − x)
to remove the denominator, rearrange to get x on one side, and solve for x.| (3.16)(0.200 − x) | = | x → 0.632 − 3.16x = x → 0.632 = 4.16x | ||
| x | = |
|
PCO = PH2O
=
0.048_0__
PCO = PH2O = 0.200 − 0.152 = 0.048 atm
atm
PCO2 = PH2
=
0.152 _0__
PCO2 = PH2 = 0.152 atm
atm
5.3-13. Re-establishing Equilibrium After an Addition
Exercise 5.14:
At a temperature near 450 °C, an equilibrium mixture in a 1.0 L flask contains
0.70 mol of HI(g) and
0.10 mol each of I2(g) and H2(g). If 0.30 mol of H2, 0.30 mol of I2, and 0.10 mol of HI are injected into this equilibrium mixture, how many moles of each gas will be present when equilibrium is re-established?
0.10 mol each of I2(g) and H2(g). If 0.30 mol of H2, 0.30 mol of I2, and 0.10 mol of HI are injected into this equilibrium mixture, how many moles of each gas will be present when equilibrium is re-established?
|
H2
|
+ |
I2
|
⇌ |
2 HI
|
|||||
|---|---|---|---|---|---|---|---|---|---|
| initial equilibrium |
0.10_0_2_
The initial equilibrium contained 0.10 mol H2.
|
0.10_0_2_
The initial equilibrium contained 0.10 mol I2.
|
0.70_0_2_
The initial equilibrium contained 0.70 mol HI.
|
mol |
K =
49_0__
K =
|
||||
| injected |
0.30_0_2_
0.30 mol H2 were injected.
|
0.30_0_2_
0.30 mol I2 were injected.
|
0.10_0_2_
0.10 mol HI were injected.
|
mol | |||||
| initial |
0.40_0_2_
There were 0.10 mol in the original equilibrium and 0.30 mol were added.
|
0.40_0_2_
There were 0.10 mol in the original equilibrium and 0.30 mol were added.
|
0.80_0_2_
There were 0.70 mol in the original equilibrium and 0.10 mol were added.
|
mol |
Q =
4.0_0_2_
Q =
|
||||
| Δ |
o_-x_s
Q < K, so H2 disappears, and its coefficient is 1, so this entry should be −x.
|
o_-x_s
Q < K, so I2 disappears, and its coefficient is 1, so this entry should be −x.
|
o_+2x_s
Q < K, so HI is formed and its coefficient is two, so the entry is +2x.
|
mol | |||||
| eq |
o_0.40-x_s
Sum the initial and Δ lines to get
0.40−x.
|
o_0.40-x_s
Sum the initial and Δ lines to get
0.40−x.
|
o_0.80+2x_s
Sum the initial and Δ lines to get
0.80+2x.
|
mol |
The equilibrium constant expression is a perfect square, so take the square root of both sides and solve for x.
x =
0.22_0_2_
Take the square root of both sides to simplify
Multiply both sides by
mol

49 =
=
| (0.80 + 2x)2 |
| (0.40 − x)(0.40 − x) |
| (0.80 + 2x)2 |
| (0.40 − x)2 |
Take the square root of both sides to simplify
7.0 =
| (0.80 + 2x) |
| (0.40 − x) |
Multiply both sides by
(0.40 − x)
to remove the denominator, rearrange to get x on one side, and solve for x.| (7.0)(0.40 − x) = 0.80 + 2x → 2.8 − 7.0x = 0.80 + 2x → 2.0 | = | 9.0x | ||
x =
| = | 0.22 |
moles of HI =
1.24_0_3_

mol HI = 0.80 + 2x = 0.80 + 2(0.22) = 1.24 mol
mol
moles of H2 = moles of I2 =
0.18_0_2_

mol H2 = mol I2 = 0.40 − x = 0.40 − 0.22 = 0.18 mol
mol
Determining the Amount to Add or Remove
5.3-14. Method
Another important calculation involves determining how much of one substance to add or remove in order to get a desired amount of one of the substances. In these cases, the unknown lies in the initial line. Sometimes, you add or remove the substance from an equilibrium mixture, but the equilibrium mixture cannot be the initial line because nothing would happen if it were at equilibrium. However, adding or removing a substance from an equilibrium line makes it an initial line. Remember that you will have only one unknown in each problem, so there are no other unknowns if one is already in the initial line.5.3-15. Percent Yield
Exercise 5.15:
At 700 K, the equilibrium constant for H2 + I2 ⇌ 2 HI is 49.0. How many moles of H2 would have to be added to 1.00 mol I2 in a 1.00 L flask to get a 90.0% yield? Use x for the number of
moles to be added.
|
H2
|
+ |
I2
|
⇌ |
2 HI
|
WaTeX parsing error. | |
|---|---|---|---|---|---|---|
| initial |
o_x_s
This is the unknown, so enter x for the initial number of moles of H2 needed.
|
1.00_0_3_
There is 1.00 mol initially.
|
0_0__
There is no HI initially.
|
mol | ||
| Δ |
-0.900_0_3_
The number of moles of H2 that react is the same as the number of moles of I2 that react.
|
-0.900_0_3_
90.0% of the I2 disappears.
|
+1.80_0_3_
The number of moles of HI that form must be twice the number of moles of I2 that react.
|
mol | ||
| eq |
o_x-0.90_s
Sum the initial and Δ lines to get
x−0.90.
|
0.10_0_2_
Sum the initial and Δ lines to get
1.00 − 0.90 = 0.10.
|
1.80_0__
Sum the initial and Δ lines to get 1.80.
|
mol |
x =
1.56_0__
Set up the equilibrium constant expression:
Rearrange to move x out of the denominator:
Solve for x:
49.0 =
| (1.80)2 |
| (x − 0.90)(0.10) |
Rearrange to move x out of the denominator:
x − 0.90 =
= 0.66
| (1.80)2 |
| (49.0)(0.10) |
Solve for x:
x = 0.66 + 0.90 = 1.56 mol
mol H2 must be added
5.3-16. Adding Reactants to Shift Equilibrium to Desired Position
Exercise 5.16:
An equilibrium mixture in a 1.00 L flask at some temperature was found to contain 0.0500 mol of SO2, 0.0250 mol of O2, and 0.0180 mol of SO3. How many moles of O2 should be added to this equilibrium mixture to double the number of moles of SO3 at equilibrium?
Note that Δng does not equal zero, so the problem must be done in molarity. However, the reaction takes place in a 1.00 L flask, so the molarity of each gas equals the number of moles.
|
2 SO2
|
+ |
O2
|
⇌ |
2 SO3
|
||
|---|---|---|---|---|---|---|
| initial |
0.0500_0_3_
No SO2 was added, so the number of moles is unchanged from the original equilibrium.
|
o_0.0250+x_s
Add the unknown number of moles to the original equilibrium number to obtain
0.025+x.
|
0.0180_0_3_
No SO3 was added, so the number of moles is unchanged from the original equilibrium.
|
M | ||
| Δ |
-0.0180_0_3_
The number of moles of SO2 that react is the same as the number of moles of SO3 that form.
|
-0.00900_0_3_
The number of moles of O2 that react is half the number of SO3 that form.
|
o_+0.0180_s
The number of moles of SO3 must double, so the number of moles formed must equal the original number.
|
M | ||
| eq |
0.0320_0_3_
Sum the initial and Δ lines to get
0.0500 − 0.0180 = 0.0320 mol.
|
o_0.0160+x_s
Sum the initial and Δ lines to get
0.0250 + x − 0.00900 = 0.0160+x mol.
|
0.0360_0_3_
Add the initial and Δ lines to get 0.0360 mol, which is twice the original amount.
|
M |
Kc =
5.18_0__

Kc =
= 5.18 M−1
M–1
| (0.0180 M)2 |
| (0.0500 M)2(0.0250 M) |
The number of moles of O2 that must be added =
0.228_0__
Set up the equilibrium constant expression:
Rearrange to move x out of the denominator:
Solve for x:
mol

5.18 =
| (0.036)2 |
| (0.032)2(0.0160 + x) |
Rearrange to move x out of the denominator:
0.0160 + x =
= 0.244
| (0.036)2 |
| (5.18)(0.032)2 |
Solve for x:
| x = 0.244 M − 0.016 M | = | 0.228 M |
| (1.00 L)(0.228 M) | = | 0.228 mol |
Putting it Together
5.3-17. Mixing an Acid and a Base
Exercise 5.17:
100. mL of a 0.10 M solution of KF and 100. mL of a 0.10 M solution of HNO2 are mixed.
What are the equilibrium concentrations in the final solution?
|
F1−(aq)
|
+ |
HNO2(aq)
|
⇌ |
HF(aq)
|
+ | NO21–(g) |
K = 0.56
|
|
|---|---|---|---|---|---|---|---|---|
| initial |
0.050_0_2_
The initial concentration is 0.050 M due to the dilution of the original solutions caused by mixing them.
|
0.050_0_2_
The initial concentration is 0.050 M due to the dilution of the original solutions caused by mixing them.
|
0_0__
The initial concentration is 0.
|
0_0__
The initial concentration is 0.
|
M | |||
| Δ |
o_-x_s
F1– disappears and its coefficient is one, so the entry is
−x.
|
o_-x_s
HNO2 disappears and its coefficient is one, so the entry is
−x.
|
o_+x_s
HF forms and its coefficient is one, so the entry is
+x.
|
o_+x_s
NO21– forms and its coefficient is one, so the entry is
+x.
|
M | |||
| eq |
o_0.050-x_s
Sum the initial and final lines to obtain
0.050−x.
|
o_0.050-x_s
Sum the initial and final lines to obtain
0.050−x.
|
o_x_s
Sum the initial and final lines to obtain x.
|
o_x_s
Sum the initial and final lines to obtain x.
|
M |
The equilibrium constant expression is a perfect square, so take the square root of both sides and solve for x.
x =
0.021_0__
Take the square root of both sides to simplify.
Multiply both sides by
M

0.56 =
=
| (x)(x) |
| (0.050 − x)(0.050 − x) |
| (x)2 |
| (0.050 − x)2 |
Take the square root of both sides to simplify.
0.75 =
| x |
| 0.50 − x |
Multiply both sides by
(0.050 − x)
to remove the denominator, rearrange to get x on one side, and solve for x.| (0.75)(0.050 − x) | = | x → 0.0375 − 0.75x = x → 0.0375 = 1.75x | ||
| x | = |
|
[F1–] = [HNO2] =
0.029 _0__

[F1−] = [HNO2] = 0.050 − x
M
[HF] = [NO21–] =
0.021_0__

[HF] = [NO21–] = x
M
Exercise 5.18:
The equilibrium mixture in the previous exercise was
[F1−] = [HNO2] = 0.029 M
and [HF] = [NO21–] = 0.021 M.
By how much should the fluoride ion concentration be increased to increase the HF concentration to 0.040 M?
|
F1−(aq)
|
+ |
HNO2(aq)
|
⇌ |
HF(aq)
|
+ | NO21–(g) |
K = 0.56
|
|
|---|---|---|---|---|---|---|---|---|
| initial |
o_0.029+x_s
The initial concentration is 0.029 M plus the unknown number of moles/liter that must be added.
|
0.029_0__
The initial concentration is given as 0.029 M.
|
0.021_0__
The initial concentration is given as 0.021 M.
|
0.021_0__
The initial concentration is given as 0.021 M.
|
M | |||
| Δ |
-0.019_0__
The number of moles/L of F1– that reacts equals the number of moles/liter of HF that are produced.
|
-0.019_0__
The number of moles/L of HNO2 that reacts equals the number of moles/liter of HF that are produced.
|
o_+0.019_s
[HF] = 0.021 M initially, but it must be 0.040 M in the final solution. Thus, it must increase by +0.019 moles/L.
|
o_+0.019_s
The number of moles/L of NO21– that are produced equals the number of moles/liter of HF that are produced.
|
M | |||
| eq |
o_0.010+x_s
Sum the initial and final lines to obtain
0.010+x.
|
0.010_0_2_
Sum the initial and final lines to obtain 0.010.
|
0.040_0_2_
The final concentration of HF is given.
|
0.040_0_2_
Sum the initial and final lines to obtain 0.040.
|
M |
Solve the equilibrium expression for x.
x =
0.28_0__
Rearrange to get the unknown out of the denominator.
Solve for x:
0.56 =
| (0.040)(0.040) |
| (0.010 + x)(0.010) |
Rearrange to get the unknown out of the denominator.
0.010 + x =
= 0.29
| (0.040)(0.040) |
| (0.56)(0.010) |
Solve for x:
x = 0.29 − 0.01 = 0.28 mol/L
mol/L fluoride ion must be added


