This summary presents an abridged version of the chapter, including the important equations and all available learning aids. For convenient reference, the learning aids (including the text’s examples) are placed next to or immediately after the relevant equation or discussion.
Topic
|
Discussion
|
Learning Aids
| |
|
10.1 The Ideal Spring and Simple Harmonic Motion
|
|
|
The force that must be applied to stretch or compress an ideal spring is
|
|
Force applied to an ideal spring
|
 | (10.1) |  |
|
Examples 1, 2
|
|
where k is the spring constant and x is the displacement of the spring from its unstrained length.
|
Interactive Solution 10.9
|
|
A spring exerts a restoring force on an object attached to the spring. The restoring force F produced by an ideal spring is
|
|
Restoring force of an ideal spring
|
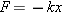 | (10.2) |  |
|
|
|
where the minus sign indicates that the restoring force points opposite to the displacement of the spring.
|
|
Simple harmonic motion
|
Simple harmonic motion is the oscillatory motion that occurs when a restoring force of the form F = = –kx acts on an object. A graphical record of position versus time for an object in simple harmonic motion is sinusoidal. The amplitude A of the motion is the maximum distance that the object moves away from its equilibrium position. –kx acts on an object. A graphical record of position versus time for an object in simple harmonic motion is sinusoidal. The amplitude A of the motion is the maximum distance that the object moves away from its equilibrium position.
|
|
Amplitude
|
|
|
|
10.2 Simple Harmonic Motion and the Reference Circle
|
|
|
The period T of simple harmonic motion is the time required to complete one cycle of the motion, and the frequency f is the number of cycles per second that occurs. Frequency and period are related according to
|
|
Period and frequency
|
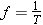 | (10.5) |  |
|
|
|
The frequency f (in Hz) is related to the angular frequency w (in rad/s) according to
|
|
Angular frequency
|
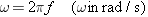 | (10.6) |  |
|
|
|
The maximum speed of an object in simple harmonic motion is
|
|
Maximum speed
|
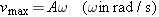 | (10.8) |  |
|
Examples 3, 4
|
|
where A is the amplitude of the motion.
|
|
|
The maximum acceleration of an object in simple harmonic motion is
|
Example 5
|
Maximum acceleration
|
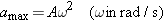 | (10.10) |  |
|
Interactive Solution 10.75
|
|
The angular frequency of simple harmonic motion is
|
Examples 6, 14
|
Angular frequency of simple harmonic motion
|
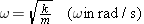 | (10.11) |  |
|
Interactive LearningWare 10.1
|
Use Self-Assessment Test 10.1 to evaluate your understanding of Sections 10.1 and 10.2.
|
|
10.3 Energy and Simple Harmonic Motion
|
|
|
The elastic potential energy of an object attached to an ideal spring is
|
|
Elastic potential energy
|
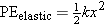 | (10.13) |  |
|
|
|
The total mechanical energy E of such a system is the sum of its translational and rotational kinetic energies, gravitational potential energy, and elastic potential energy:
|
Examples 7, 8, 9, 15
|
Total mechanical energy
|
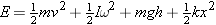 | (10.14) |  |
|
Interactive LearningWare 10.2
|
|
If external nonconservative forces like friction do no net work, the total mechanical energy of the system is conserved:
|
Concept Simulation 10.1
|
Conservation of mechanical energy
|
|
Interactive Solutions 10.31, 10.35, 10.77
|
|
10.4 The Pendulum
|
|
|
A simple pendulum is a particle of mass m attached to a frictionless pivot by a cable whose length is L and whose mass is negligible. The small-angle (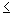 10°) back-and-forth swinging of a simple pendulum is simple harmonic motion, but large-angle movement is not. The frequency f of the motion is given by 10°) back-and-forth swinging of a simple pendulum is simple harmonic motion, but large-angle movement is not. The frequency f of the motion is given by
|
Concept Simulation 10.2
|
Frequency of a simple pendulum
|
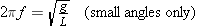 | (10.16) |  |
|
Example 10
|
|
A physical pendulum consists of a rigid object, with moment of inertia I and mass m, suspended from a frictionless pivot. For small-angle displacements, the frequency f of simple harmonic motion for a physical pendulum is given by
|
|
Frequency of a physical pendulum
|
 | (10.15) |  |
|
Example 11
|
|
where L is the distance between the axis of rotation and the center of gravity of the rigid object.
|
|
|
10.5 Damped Harmonic Motion
|
|
Damped harmonic motion
Critical damping
|
Damped harmonic motion is motion in which the amplitude of oscillation decreases as time passes. Critical damping is the minimum degree of damping that eliminates any oscillations in the motion as the object returns to its equilibrium position.
|
Concept Simulation 10.3
|
|
10.6 Driven Harmonic Motion and Resonance
|
|
Damped harmonic motion Resonance
|
Driven harmonic motion occurs when a driving force acts on an object along with the restoring force. Resonance is the condition under which the driving force can transmit large amounts of energy to an oscillating object, leading to large-amplitude motion. In the absence of damping, resonance occurs when the frequency of the driving force matches a natural frequency at which the object oscillates.
|
|
|
10.7 Elastic Deformation
|
|
|
One type of elastic deformation is stretch and compression. The magnitude F of the force required to stretch or compress an object of length L0 and cross-sectional area A by an amount DL is (see Figure 10.29)
|
|
Young’s modulus
|
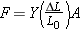 | (10.17) |  |
|
Example 12
|
|
where Y is a constant called Young’s modulus.
|
|
|
Another type of elastic deformation is shear. The magnitude F of the shearing force required to create an amount of shear DX for an object of thickness L0 and cross-sectional area A is (see Figure 10.31)
|
|
Shear modulus
|
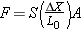 | (10.18) |  |
|
Example 13
|
|
where S is a constant called the shear modulus.
|
|
|
A third type of elastic deformation is volume deformation, which has to do with pressure. The pressure P is the magnitude F of the force acting perpendicular to a surface divided by the area A over which the force acts:
|
|
Pressure
|
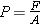 | (10.19) |  |
|
|
|
The SI unit for pressure is N/m2, a unit known as a pascal (Pa): 1 Pa = = 1 N/m2. 1 N/m2.
|
|
|
The change DP in pressure needed to change the volume V0 of an object by an amount DV is (see Figure 10.33)
|
|
Bulk modulus
|
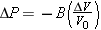 | (10.20) |  |
|
|
|
where B is a constant known as the bulk modulus.
|
|
|
10.8 Stress, Strain, and Hooke’s Law
|
|
Stress and Strain
Hooke’s Law
|
Stress is the magnitude of the force per unit area applied to an object and causes strain. For stretch/compression, the strain is the fractional change DL/L0 in length. For shear, the strain reflects the change in shape of the object and is given by DX/L0 (see Figure 10.31). For volume deformation, the strain is the fractional change in volume DV/V0. Hooke’s law states that stress is directly proportional to strain
|
|
Use Self-Assessment Test 10.2 to evaluate your understanding of Sections 10.3, 10.4, 10.5, 10.6, 10.7 and 10.8.
|

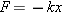
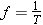
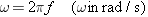
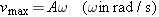
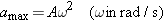
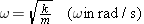
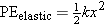
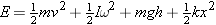
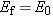
 10°) back-and-forth swinging of a simple pendulum is simple harmonic motion, but large-angle movement is not. The frequency f of the motion is given by
10°) back-and-forth swinging of a simple pendulum is simple harmonic motion, but large-angle movement is not. The frequency f of the motion is given by 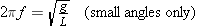

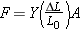
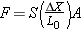
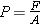
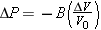
 10°) back-and-forth swinging of a simple pendulum is simple harmonic motion, but large-angle movement is not. The frequency f of the motion is given by
10°) back-and-forth swinging of a simple pendulum is simple harmonic motion, but large-angle movement is not. The frequency f of the motion is given by